|
Здравствуйте! Записался на ваш курс, но не понимаю как произвести оплату. Надо ли писать заявление и, если да, то куда отправлять? как я получу диплом о профессиональной переподготовке? |
Основные понятия информационной безопасности
Криптография как одна из базовых технологий безопасности ОС
Многие службы информационной безопасности, такие как контроль входа в систему, разграничение доступа к ресурсам, обеспечение безопасного хранения данных и ряд других, опираются на использование криптографических алгоритмов. Имеется обширная литература по этому актуальному для безопасности информационных систем вопросу.
Шифрование – процесс преобразования сообщения из открытого текста (plaintext) в шифротекст (ciphertext) таким образом, чтобы:
- его могли прочитать только те стороны, для которых оно предназначено;
- проверить подлинность отправителя (аутентификация);
- гарантировать, что отправитель действительно послал данное сообщение.
В алгоритмах шифрования предусматривается наличие ключа. Ключ – это некий параметр, не зависящий от открытого текста. Результат применения алгоритма шифрования зависит от используемого ключа. В криптографии принято правило Кирхгофа: "Стойкость шифра должна определяться только секретностью ключа". Правило Кирхгофа подразумевает, что алгоритмы шифрования должны быть открыты.
В методе шифрования с секретным или симметричным ключом имеется один ключ, который используется как для шифрования, так и для расшифровки сообщения. Такой ключ нужно хранить в секрете. Это затрудняет использование системы шифрования, поскольку ключи должны регулярно меняться, для чего требуется их секретное распространение. Наиболее популярные алгоритмы шифрования с секретным ключом: DES, TripleDES, ГОСТ и ряд других.
Часто используется шифрование с помощью односторонней функции, называемой также хеш- или дайджест-функцией. Применение этой функции к шифруемым данным позволяет сформировать небольшой дайджест из нескольких байтов, по которому невозможно восстановить исходный текст. Получатель сообщения может проверить целостность данных, сравнивая полученный вместе с сообщением дайджест с вычисленным вновь при помощи той же односторонней функции. Эта техника активно используется для контроля входа в систему. Например, пароли пользователей хранятся на диске в зашифрованном односторонней функцией виде. Наиболее популярные хеш-функции: MD4, MD5 и др.
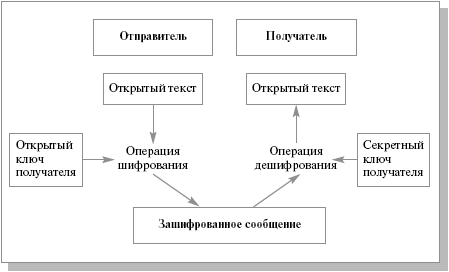
В системах шифрования с открытым или асимметричным ключом (public/ assymmetric key) используется два ключа (см. рис. 15.1). Один из ключей, называемый открытым, несекретным, используется для шифрования сообщений, которые могут быть расшифрованы только с помощью секретного ключа, имеющегося у получателя, для которого предназначено сообщение. Иногда поступают по-другому. Для шифрования сообщения используется секретный ключ, и если сообщение можно расшифровать с помощью открытого ключа, подлинность отправителя будет гарантирована (система электронной подписи). Этот принцип изобретен Уитфилдом Диффи (Whitfield Diffie) и Мартином Хеллманом (Martin Hellman) в 1976 г.
Использование открытых ключей снимает проблему обмена и хранения ключей, свойственную системам с симметричными ключами. Открытые ключи могут храниться публично, и каждый может послать зашифрованное открытым ключом сообщение владельцу ключа. Однако расшифровать это сообщение может только владелец открытого ключа при помощи своего секретного ключа, и никто другой. Несмотря на очевидные удобства, связанные с хранением и распространением ключей, асимметричные алгоритмы гораздо менее эффективны, чем симметричные, поэтому во многих криптографических системах используются оба метода.
Среди несимметричных алгоритмов наиболее известен RSA, предложенный Роном Ривестом (Ron Rivest), Ади Шамиром (Adi Shamir) и Леонардом Эдлманом (Leonard Adleman). Рассмотрим его более подробно.
Шифрование с использованием алгоритма RSA
Идея, положенная в основу метода, состоит в том, чтобы найти такую
функцию 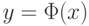 , для которой получение обратной функции
, для которой получение обратной функции 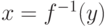 было
бы в общем случае очень сложной задачей (NP-полной задачей).
Например, получить произведение двух чисел
было
бы в общем случае очень сложной задачей (NP-полной задачей).
Например, получить произведение двух чисел 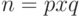 просто, а разложить
просто, а разложить  на множители, если
на множители, если  и
и  достаточно большие простые числа, –
NP-полная задача с вычислительной сложностью
достаточно большие простые числа, –
NP-полная задача с вычислительной сложностью 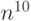 . Однако если знать
некую секретную информацию, то найти обратную функцию
. Однако если знать
некую секретную информацию, то найти обратную функцию 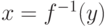 существенно проще. Такие функции также называют односторонними
функциями с лазейкой или потайным ходом.
существенно проще. Такие функции также называют односторонними
функциями с лазейкой или потайным ходом.
Применяемые в RSA прямая и обратная функции просты. Они базируются на применении теоремы Эйлера из теории чисел.
Прежде чем сформулировать теорему Эйлера, необходимо определить
важную функцию 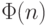 из теории чисел, называемую функцией Эйлера. Это
число взаимно простых (взаимно простыми называются целые числа, не
имеющие общих делителей) с
из теории чисел, называемую функцией Эйлера. Это
число взаимно простых (взаимно простыми называются целые числа, не
имеющие общих делителей) с  целых чисел, меньших
целых чисел, меньших  . Например,
. Например,  . Очевидно, что, если
. Очевидно, что, если  и
и  – простые числа и
– простые числа и  , то
, то 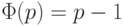 ,
и
,
и 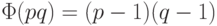 .
.
Теорема Эйлера
Теорема Эйлера утверждает, что для любых взаимно простых чисел  и
и 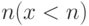

или в более общем виде
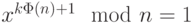
Сформулируем еще один важный результат. Для любого  и
и 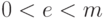 , где
, где  и
и  взаимно просты, найдется единственное
взаимно просты, найдется единственное 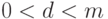 , такое, что
, такое, что
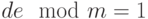 .
.
Здесь  легко можно найти по обобщенному алгоритму Евклида (см.,
например, Д. Кнут. Искусство программирования на ЭВМ, т.2, 4.5.2).
Известно, что вычислительная сложность алгоритма Евклида
легко можно найти по обобщенному алгоритму Евклида (см.,
например, Д. Кнут. Искусство программирования на ЭВМ, т.2, 4.5.2).
Известно, что вычислительная сложность алгоритма Евклида  .
.
Подставляя 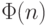 вместо
вместо  , получим
, получим 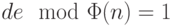
или
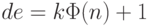
Тогда прямой функцией будет
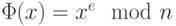
где  – положительное целое,
– положительное целое, 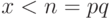 ,
,  и
и  – целые простые числа и,
следовательно,
– целые простые числа и,
следовательно,

где  – положительное целое и
– положительное целое и 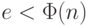 . Здесь
. Здесь  и
и  открыты. Однако
открыты. Однако  и
и  неизвестны (чтобы их найти, нужно выполнить разбиение
неизвестны (чтобы их найти, нужно выполнить разбиение  на
множители), следовательно, неизвестна и
на
множители), следовательно, неизвестна и 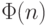 , а именно они и
составляют потайной ход.
, а именно они и
составляют потайной ход.
Вычислим обратную функцию
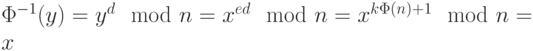
Последнее преобразование справедливо, поскольку  и
и  и
и  взаимно
просты.
взаимно
просты.
При практическом использовании алгоритма RSA вначале необходимо выполнить генерацию ключей. Для этого нужно:
- Выбрать два очень больших простых числа
 и
и  ;
; - Вычислить произведение
 ;
; - Выбрать большое случайное число d, не имеющее общих сомножителей с
числом
 ;
; - Определить число
 , чтобы выполнялось
, чтобы выполнялось .
.
Тогда открытым ключом будут числа  и
и  , а секретным ключом – числа
, а секретным ключом – числа  и
и  .
.
Теперь, чтобы зашифровать данные по известному ключу 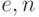 ,
необходимо сделать следующее.
,
необходимо сделать следующее.
- Разбить шифруемый текст на блоки, где i-й блок представить в виде
числа
 , величина которого меньше, чем
, величина которого меньше, чем  . Это можно сделать
различными способами, например используя вместо букв их номера в
алфавите.
. Это можно сделать
различными способами, например используя вместо букв их номера в
алфавите. - Зашифровать текст, рассматриваемый как последовательность чисел
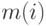 , по формуле
, по формуле 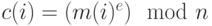 .
.
Чтобы расшифровать эти данные, используя секретный ключ 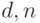 ,
необходимо вычислить:
,
необходимо вычислить: 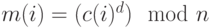 . В результате будет
получено множество чисел
. В результате будет
получено множество чисел 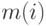 , которые представляют собой часть
исходного текста.
, которые представляют собой часть
исходного текста.
Например, зашифруем и расшифруем сообщение 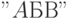 , которое представим
как число
, которое представим
как число 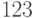 .
.
Выбираем  и
и 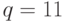 (числа на самом деле должны быть большими).
(числа на самом деле должны быть большими).
Находим 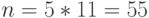 .
.
Определяем 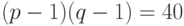 . Тогда
. Тогда  будет равно, например,
будет равно, например,  .
.
Выберем  , исходя из
, исходя из  . Например,
. Например, 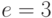 .
.
Теперь зашифруем сообщение, используя открытый ключ 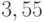

Теперь расшифруем эти данные, используя закрытый ключ  .
.
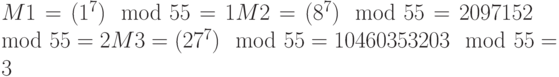
Таким образом, все данные расшифрованы.
Заключение
Информационная безопасность относится к числу дисциплин, развивающихся чрезвычайно быстрыми темпами. Только комплексный, систематический, современный подход способен успешно противостоять нарастающим угрозам.
Ключевые понятия информационной безопасности: конфиденциальность, целостность и доступность информации, а любое действие, направленное на их нарушение, называется угрозой.
Основные понятия информационной безопасности регламентированы в основополагающих документах.
Существует несколько базовых технологий безопасности, среди которых можно выделить криптографию.