Восходящие анализаторы

LR(1)-анализатор

LR(1)-анализатор использует для принятия решения один символ входной цепочки. Алгоритм построения управляющей таблицы LR(1)-анализатора подобен уже рассмотренному алгоритму для LR (0)-анализатора, но понятие ситуации в LR(1)-анализаторе более сложное: LR(1)-ситуация состоит из правила грамматики, позиции правой части (представляемой точкой) и одного символа входной строки (lookahead symbol). LR(1)-ситуация выглядит следующим образом: [A-> w₁ . w₂ , a] , где a - терминальный символ. Ситуация [A-> w₁ .w₂, a] означает, что цепочка w₁ находится на вершине магазина, и префикс входной цепочки выводим из цепочки w₂ x. Как и прежде, состояние автомата определяется множеством ситуаций. Для построения управляющей таблицы необходимо переопределить базовые операции closure и goto.

closure (I) {
   do {
      Iold =I;
      for (каждой ситуации [A-> w1.Xw2, z] из I)
         for (любого правила X-> u)
            for (любой цепочки w, принадлежащей FIRST (w2 z))
               I+=[X->.u, w];
   } while (I != Iold);
   return I;
}
goto (I, X) {
   J = {};
   for (каждой ситуации [A-> w1.Xw2, z] из I)
      J+=[A-> w1 X.w2, z];
   return closure (J);
}

Естественно, операция reduce также зависит от символа входной цепочки:

R=[]
foreach (I из T)
   foreach ([A->w., z] из I)
      R+={(I, z, A->w)}

Тройка (I, z, A->w) означает, что в состоянии I для символа z входной цепочки анализатор будет осуществлять свертку по правилу A->w.

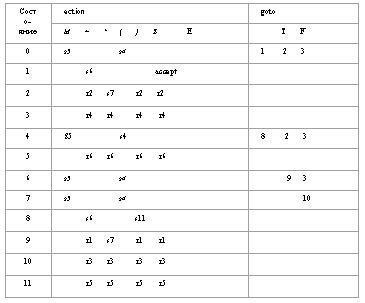
Управляющая таблица LR(1)-анализатора

Управляющая таблица LR(1)-анализатора

Построим управляющую таблицу анализатора для следующей грамматики:

E -> E+T 
E  ->  T
T ->  T*F 
T ->  F
F ->  (E) 
F ->  id

Пример. Рассмотрим грамматику:

(1)	E+T
(2)	E->T
(3)	T->T*F
(4)	T->F
(5)	F-> (E)
(6)	F->id

Управляющая таблица для такой грамматики выглядит следующим образом:

Как обычно,

• si - перенос и переход в состояние i
• ri - свертка по правилу i
• i - переход в состояние i

LALR(1)-анализатор

Таблицы LR(1)-анализатора могут оказаться очень большими, ведь даже маленькая грамматика нашего примера привела к автомату с двенадцатью состояниями. Таблицы меньшего размера можно получить путем слияния любых двух состояний, которые совпадают с точностью до символов входной строки (lookahead symbols).

Пример.Рассмотрим грамматику G₁ с правилами:

S -> AA
A -> aA
A -> b

Пополним эту грамматику правилом S' -> S.

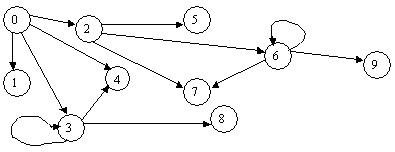
Для этой грамматики мы получим следующие состояния:

0: {[S'->.S, $], [S->.AA, $], [A->.aA, a], [A->.aA, b], [A->.b, a], [A->.b, b]}
1: {[S'->S., $]}
2: {[S'->A.A, $], A->.aA, $], [A->.b, $]}
3: {[A->a.A, a], [A->a.A, b], [A->.a.A, a], [A->.a.A, b], [A->.b, a], [A->.b, b]}
4: {[A->b., a], [A->b., b]}
5: {[S->AA. $]}
6: {[A->a.A, $], [A->.aA, $], [A->.b, $]}
7:  {[A->b., $]}
8:  {[A->aA.,a], [A->aA.,b]}
9:  {[A->aA.,$]}

Граф переходов выглядит так: