|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Теоретическая база прикладной статистики
4.3. Теоремы о наследовании сходимости
Суть проблемы наследования сходимости. Пусть распределения случайных величин 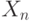 при
при 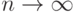 стремятся к распределению случайной величины
стремятся к распределению случайной величины  . При каких функциях
. При каких функциях  можно утверждать, что распределения случайных величин
можно утверждать, что распределения случайных величин 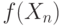 сходятся к распределению
сходятся к распределению 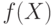 , т.е. наследуется сходимость?
, т.е. наследуется сходимость?
Хорошо известно, что для непрерывных функций  сходимость наследуется [
[
4.23
]
]. Однако в прикладной статистике используются различные обобщения этого утверждения. Необходимость обобщений связана с тремя обстоятельствами:
сходимость наследуется [
[
4.23
]
]. Однако в прикладной статистике используются различные обобщения этого утверждения. Необходимость обобщений связана с тремя обстоятельствами:
- статистические данные могут моделироваться не только случайными величинами, но и случайными векторами, случайными множествами, случайными элементами произвольной природы (т.е. функциями на вероятностном пространстве со значениями в произвольном множестве);
- переход к пределу должен рассматриваться не только для случая безграничного возрастания объема выборки, но и в более общих случаях. Например, если в постановке статистической задачи участвуют несколько выборок объемов
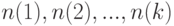 , то вполне обычным является предположение о безграничном росте всех этих объемов (что можно описать и как
, то вполне обычным является предположение о безграничном росте всех этих объемов (что можно описать и как 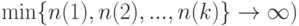 ;
; - функция
 не обязательно является непрерывной. Она может иметь разрывы. Кроме того, она может зависеть от параметров, по которым происходит переход к пределу, например, может зависеть от объемов выборок. Так, в
"Статистический анализ числовых величин"
понадобится рассмотреть функцию
не обязательно является непрерывной. Она может иметь разрывы. Кроме того, она может зависеть от параметров, по которым происходит переход к пределу, например, может зависеть от объемов выборок. Так, в
"Статистический анализ числовых величин"
понадобится рассмотреть функцию 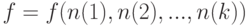 .
.
Расстояние Прохорова и сходимость по направленному множеству. Введем необходимые для дальнейшего изложения понятия.
Расстояние (метрика) Прохорова. Пусть  - некоторое пространство,
- некоторое пространство,  - его подмножество,
- его подмножество,  - метрика в
- метрика в  . Введем понятие
. Введем понятие  -окрестности множества
-окрестности множества  в метрике
в метрике  :
:

Таким образом,  -окрестность множества
-окрестность множества  - это совокупность всех точек пространства
- это совокупность всех точек пространства  , отстоящих от
, отстоящих от  не более чем на положительное число
не более чем на положительное число  . При этом расстояние от точки
. При этом расстояние от точки  до множества
до множества  - это точная нижняя грань расстояний от
- это точная нижняя грань расстояний от  до точек множества
до точек множества  , т.е.
, т.е.

Пусть 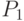 и
и 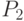 - две вероятностные меры на
- две вероятностные меры на  (т.е. распределения двух случайных элементов со значениями в
(т.е. распределения двух случайных элементов со значениями в  ). Пусть
). Пусть  - множество чисел
- множество чисел 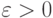 таких, что
таких, что

 пространства
пространства  ). Пусть
). Пусть 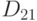 - множество чисел
- множество чисел 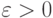 таких, что
таких, что
 пространства
пространства  . Расстояние Прохорова
. Расстояние Прохорова  между вероятностными мерами (его можно рассматривать и как расстояние между случайными элементами с распределениями
между вероятностными мерами (его можно рассматривать и как расстояние между случайными элементами с распределениями 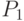 и
и 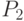 соответственно) вводится формулой
соответственно) вводится формулой
С помощью метрики Прохорова формализуется понятие сходимости распределений случайных элементов в произвольном пространстве.
Расстояние  введено академиком РАН Юрием Васильевичем Прохоровым в середине ХХ в. и широко используется в современной теории вероятностей.
введено академиком РАН Юрием Васильевичем Прохоровым в середине ХХ в. и широко используется в современной теории вероятностей.
Сходимость по направленному множеству [
[
4.11
]
, с.95 - 96]. Бинарное отношение 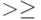 (упорядочение), заданное на множестве
(упорядочение), заданное на множестве  , называется направлением на нем, если
, называется направлением на нем, если  не пусто и
не пусто и
(а) если 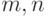 и
и  - такие элементы множества
- такие элементы множества  , что
, что  и
и  , то
, то  ;
;
(б)  для любого
для любого  из
из  ;
;
(в) если  и
и  принадлежат
принадлежат  , то найдется элемент
, то найдется элемент  из
из  такой, что
такой, что  и
и  .
.
Направленное множество - это пара 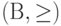 , где
, где  > - направление на множестве
> - направление на множестве  . Направленностью (или "последовательностью по направленному множеству") называется пара
. Направленностью (или "последовательностью по направленному множеству") называется пара 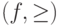 , где
, где  - функция,
- функция,  - направление на ее области определения. Пусть
- направление на ее области определения. Пусть 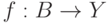 , где
, где  - топологическое пространство. Направленность
- топологическое пространство. Направленность 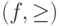 сходится в топологическом пространстве
сходится в топологическом пространстве  к точке
к точке  , если для любой окрестности
, если для любой окрестности  точки
точки  найдется
найдется  из
из  такое, что
такое, что  при любом
при любом  . В таком случае говорят также о сходимости по направленному множеству.
. В таком случае говорят также о сходимости по направленному множеству.
Пусть 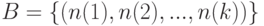 - совокупность векторов, каждый из которых составлен из объемов
- совокупность векторов, каждый из которых составлен из объемов  выборок. Пусть
выборок. Пусть
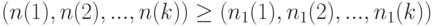
 при всех
при всех 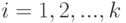 . Тогда
. Тогда 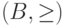 - направленное множество, сходимость по которому эквивалентна сходимости при
- направленное множество, сходимость по которому эквивалентна сходимости при 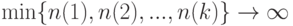 .
.Чтобы охватить различные частные случаи, целесообразно предельные теоремы формулировать в терминах сходимости по направленному множеству. Будем писать  . Пусть запись
. Пусть запись 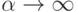 обозначает переход к пределу по направленному множеству.
обозначает переход к пределу по направленному множеству.
Формулировка проблемы наследования сходимости. Пусть случайные элементы  со значениями в пространстве
со значениями в пространстве  сходятся при
сходятся при 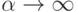 к случайному элементу
к случайному элементу  , где через
, где через 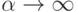 обозначен переход к пределу по направленному множеству. Сходимость случайных элементов означает, что
обозначен переход к пределу по направленному множеству. Сходимость случайных элементов означает, что 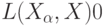 при
при 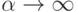 , где
, где  - метрика Прохорова в пространстве
- метрика Прохорова в пространстве  .
.
Пусть 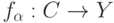 - некоторые функции. Какие условия надо на них наложить, чтобы из
- некоторые функции. Какие условия надо на них наложить, чтобы из 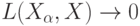 вытекало, что
вытекало, что 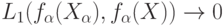 при
при 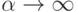 , где
, где 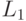 - метрика Прохорова в пространстве
- метрика Прохорова в пространстве  ? Другими словами, какие условия на функции
? Другими словами, какие условия на функции 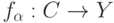 гарантируют наследование сходимости?
гарантируют наследование сходимости?
В работах [
[
1.15
]
,
[
4.19
]
] найдены необходимые и достаточные условия на функции 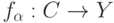 , гарантирующие наследование сходимости. Описанию этих условий посвящена оставшаяся часть данного пункта.
, гарантирующие наследование сходимости. Описанию этих условий посвящена оставшаяся часть данного пункта.
Приведем для полноты изложения строгие формулировки математических предположений (в дальнейшем никому, кроме профессиональных математиков, не понадобятся).
Математические предположения. Пусть  и
и  - полные сепарабельные метрические пространства. Пусть выполнены обычные предположения измеримости:
- полные сепарабельные метрические пространства. Пусть выполнены обычные предположения измеримости:  и
и  - случайные элементы
- случайные элементы 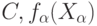 и
и 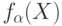 - случайные элементы в
- случайные элементы в  , рассматриваемые ниже подмножества пространств
, рассматриваемые ниже подмножества пространств  и
и  лежат в соответствующих
лежат в соответствующих  -алгебрах измеримых подмножеств, и т.д.
-алгебрах измеримых подмножеств, и т.д.
Понадобятся некоторые определения. Разбиение 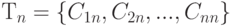 пространства
пространства  - это такой набор подмножеств
- это такой набор подмножеств 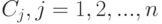 , этого пространства, что пересечение любых двух из них пусто, а объединение совпадает с
, этого пространства, что пересечение любых двух из них пусто, а объединение совпадает с  . Диаметром
. Диаметром  подмножества
подмножества  множества
множества  называется точная верхняя грань расстояний между элементами
называется точная верхняя грань расстояний между элементами  , т.е.
, т.е.

где 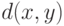 - метрика в пространстве
- метрика в пространстве  . Обозначим
. Обозначим  границу множества
границу множества  , т.е. совокупность точек х таких, что любая их окрестность
, т.е. совокупность точек х таких, что любая их окрестность 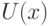 имеет непустое пересечение как с
имеет непустое пересечение как с  , так и с
, так и с 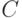 . Колебанием
. Колебанием 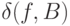 функции
функции  на подмножестве
на подмножестве  множества
множества  называется
называется 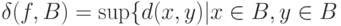 .
.
Достаточное условие для наследования сходимости. Пусть 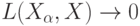 при
при 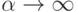 . Пусть существует последовательность
. Пусть существует последовательность 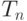 разбиений пространства
разбиений пространства  такая, что
такая, что  для любого
для любого  из
из 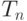 и, основное условие, для любого
и, основное условие, для любого 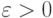
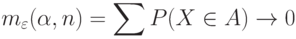 |
( 1) |
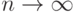 и
и 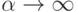 , где сумма берется по всем тем
, где сумма берется по всем тем  из
из 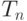 , для которых колебание функции
, для которых колебание функции  на
на  больше
больше  , т.е.
, т.е.  . Тогда
. Тогда 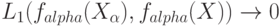 при
при 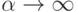 .
.Необходимое условие для наследования сходимости. Пусть  - конечномерное линейное пространство,
- конечномерное линейное пространство, 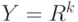 . Пусть случайные элементы
. Пусть случайные элементы 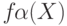 асимптотически ограничены по вероятности при
асимптотически ограничены по вероятности при 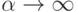 , т.е. для любого
, т.е. для любого 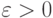 существуют число
существуют число  и элемент направленного множества
и элемент направленного множества  такие, что
такие, что  при
при 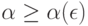 , где
, где 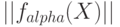 - норма (длина) вектора
- норма (длина) вектора  . Пусть существует последовательность
. Пусть существует последовательность 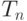 разбиений пространства
разбиений пространства  такая, что
такая, что

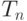 является безгранично измельчающейся. Самое существенное - пусть условие (1) не выполнено для последовательности
является безгранично измельчающейся. Самое существенное - пусть условие (1) не выполнено для последовательности 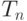 . Тогда существует последовательность случайных элементов
. Тогда существует последовательность случайных элементов  такая, что
такая, что 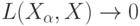 при
при 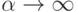 , но
, но  не сходится к 0 при
не сходится к 0 при 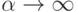 .
.Несколько огрубляя, можно сказать, что условие (1) является необходимым и достаточным для наследования сходимости.
Пример 1. Пусть  и
и  - конечномерные линейные пространства, функции
- конечномерные линейные пространства, функции 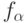 не зависят от
не зависят от  , т.е.
, т.е.  , причем функция
, причем функция  ограничена. Тогда условие (1) эквивалентно требованию интегрируемости по Риману-Стилтьесу функции
ограничена. Тогда условие (1) эквивалентно требованию интегрируемости по Риману-Стилтьесу функции  по мере
по мере 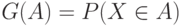 . В частности, условие (1) выполнено для непрерывной функции
. В частности, условие (1) выполнено для непрерывной функции  .
.
В конечномерных пространствах  вместо сходимости
вместо сходимости 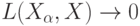 при
при 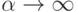 можно говорить о слабой сходимости функций распределения случайных векторов
можно говорить о слабой сходимости функций распределения случайных векторов  к функции распределения случайного вектора
к функции распределения случайного вектора  . Речь идет о "сходимости по распределению", т.е. о сходимости во всех точках непрерывности функции распределения случайного вектора
. Речь идет о "сходимости по распределению", т.е. о сходимости во всех точках непрерывности функции распределения случайного вектора  . В этом случае разбиения могут состоять из многомерных параллелепипедов [
[
1.15
]
, гл.2].
. В этом случае разбиения могут состоять из многомерных параллелепипедов [
[
1.15
]
, гл.2].
Пример 2. Полученные выше результаты дают обоснование для следующих рассуждений (ср., например, утверждения в
"Статистический анализ числовых величин"
). Пусть по двум независимым выборкам объемов  и
и  соответственно построены статистики
соответственно построены статистики 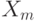 и
и 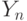 . Пусть известно, что распределения этих статистик сходятся при безграничном росте объемов выборок к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Пусть
. Пусть известно, что распределения этих статистик сходятся при безграничном росте объемов выборок к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Пусть 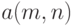 и
и 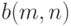 - некоторые коэффициенты. Тогда согласно результатам примера 1 распределение случайной величины
- некоторые коэффициенты. Тогда согласно результатам примера 1 распределение случайной величины 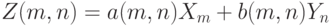 сближается с распределением нормально распределенной случайной величины с математическим ожиданием 0 и дисперсией
сближается с распределением нормально распределенной случайной величины с математическим ожиданием 0 и дисперсией  . Если же
. Если же 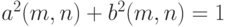 , например,
, например,
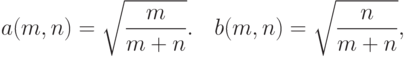
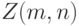 сходится при безграничном росте объемов выборок к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1.
сходится при безграничном росте объемов выборок к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1.