| Россия, Пошатово |
Порождение комбинаторных объектов
2.5. Коды Грея и аналогичные задачи
Иногда бывает полезно перечислять объекты в таком порядке, чтобы каждый следующий минимально отличался от предыдущего. Рассмотрим несколько задач такого рода.
2.5.1. Перечислить все последовательности длины n из чисел 1..k в таком порядке, чтобы каждая следующая отличалась от предыдущей в единственной цифре, причем не более, чем на 1.
Решение. Рассмотрим прямоугольную доску ширины n и высоты k. На каждой вертикали будет стоять шашка. Таким образом, положения шашек соответствуют последовательностям из чисел 1..k длины n ( s -ый член последовательности соответствует высоте шашки на s -ой вертикали). На каждой шашке нарисуем стрелочку, которая может быть направлена вверх или вниз. Вначале все шашки поставим на нижнюю горизонталь стрелочкой вверх. Далее двигаем шашки по такому правилу: найдя самую правую шашку, которую можно подвинуть в направлении (нарисованной на ней) стрелки, двигаем ее на одну клетку в этом направлении, а все стоящие правее нее шашки (они уперлись в край) разворачиваем кругом.
Ясно, что на каждом шаге только одна шашка сдвигается, т.е. один член последовательности меняется на 1. Докажем индукцией по n, что проходятся все последовательности из чисел 1..k. Случай n=1 очевиден. Пусть n>1. Все ходы поделим на те, где двигается последняя шашка, и те, где двигается не последняя. Во втором случае последняя шашка стоит у стены, и мы ее поворачиваем, так что за каждым ходом второго типа следует k-1 ходов первого типа, за время которых последняя шашка побывает во всех клетках. Если мы теперь забудем о последней шашке, то движения первых n-1 по предположению индукции пробегают все последовательности длины n-1 по одному разу; движения же последней шашки из каждой последовательности длины n-1 делают k последовательностей длины n.
В программе, помимо последовательности x[1]..x[n], будем хранить массив d[1]..d[n] из чисел +1 и -1 ( +1 соответствует стрелке вверх, -1 - стрелке вниз).
Начальное состояние: x[1]=...=x[n]=1 ; d[1]=...=d[n]=1.
Приведем алгоритм перехода к следующей последовательности (одновременно выясняется, возможен ли переход - ответ становится значением булевской переменной p ).
{если можно, сделать шаг и положить p := true, если нет,
положить p := false }
i := n;
while (i > 1) and
| (((d[i]=1) and (x[i]=n)) or ((d[i]=-1) and (x[i]=1)))
| do begin
| i:=i-1;
end;
if (d[i]=1 and x[i]=n) or (d[i]=-1 and x[i]=1) then begin
| p:=false;
end else begin
| p:=true;
| x[i] := x[i] + d[i];
| for j := i+1 to n do begin
| | d[j] := - d[j];
| end;
end;Замечание. Для последовательностей нулей и единиц возможно другое решение, использующее двоичную систему. (Именно оно связывается обычно с названием "коды Грея".)
Запишем подряд все числа от  до
до 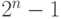 в двоичной
системе. Например, для
в двоичной
системе. Например, для 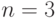 напишем:
напишем:

 ). Иными словами, число
). Иными словами, число 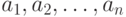 преобразуем в
преобразуем в 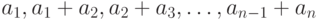 (сумма по модулю
(сумма по модулю  ). Для
). Для 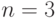 получим:
получим:
Легко проверить, что описанное преобразование чисел
обратимо (и тем самым дает все последовательности по одному
разу). Кроме того, двоичные записи соседних чисел
отличаются заменой конца 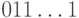 на конец
на конец 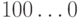 ,
что - после преобразования - приводит к изменению
единственной цифры.
,
что - после преобразования - приводит к изменению
единственной цифры.
Применение кода Грея. Пусть есть вращающаяся ось,
и мы хотим поставить датчик угла поворота этой оси. Насадим
на ось барабан, выкрасим половину барабана в черный цвет,
половину в белый и установим фотоэлемент. На его выходе
будет в половине случаев  , а в половине
, а в половине  (т.е. мы
измеряем угол "с точностью до
(т.е. мы
измеряем угол "с точностью до 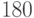 ").
").
Сделав рядом другую дорожку из двух черных и белых частей
и поставив второй фотоэлемент, получаем возможность
измерить угол с точностью до  :
:
Сделав третью,
мы измерим угол с точностью до 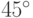 и т.д. Эта идея
имеет, однако, недостаток: в момент пересечения границ
сразу несколько фотоэлементов меняют сигнал, и если эти
изменения произойдут не совсем одновременно, на какое-то
время показания фотоэлементов будут бессмысленными. Коды
Грея позволяют избежать этой опасности. Сделаем так, чтобы
на каждом шаге менялось показание лишь одного фотоэлемента
(в том числе и на последнем, после целого оборота).
и т.д. Эта идея
имеет, однако, недостаток: в момент пересечения границ
сразу несколько фотоэлементов меняют сигнал, и если эти
изменения произойдут не совсем одновременно, на какое-то
время показания фотоэлементов будут бессмысленными. Коды
Грея позволяют избежать этой опасности. Сделаем так, чтобы
на каждом шаге менялось показание лишь одного фотоэлемента
(в том числе и на последнем, после целого оборота).
Написанная нами формула позволяет легко преобразовать данные от фотоэлементов в двоичный код угла поворота.
Заметим также, что геометрически существование кода Грея
означает наличие "гамильтонова цикла"
в  -мерном кубе (возможность обойти все вершины куба
по разу, двигаясь по ребрам, и вернуться в исходную
вершину).
-мерном кубе (возможность обойти все вершины куба
по разу, двигаясь по ребрам, и вернуться в исходную
вершину).
2.5.2. Напечатать все перестановки чисел 1..n так, чтобы каждая следующая получалась из предыдущей перестановкой (транспозицией) двух соседних чисел. Например, при n=3 допустим такой порядок:
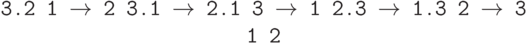
Решение. Наряду с множеством перестановок рассмотрим
множество последовательностей y[1]..y[n] целых
неотрицательных чисел, для которых ![\hbox{\texttt{y[1]}}\le \hbox{\texttt{0}}](/sites/default/files/tex_cache/c81e6738bd2ad93f219a7b32709f8dcf.png) ,
,  ,
, ![\hbox{\texttt{y[n]}}\le \hbox{\texttt{n-1}}](/sites/default/files/tex_cache/6cd8a94fdcbf4949fbe14cd7be71ab46.png) . В нем
столько же элементов, сколько в множестве всех
перестановок, и мы сейчас установим между ними взаимно
однозначное соответствие. Именно, каждой перестановке
поставим в соответствие последовательность y[1]..y[n],
где y[i] - количество чисел, меньших i и стоящих
левее i в этой перестановке. Взаимная однозначность
вытекает из такого замечания. Перестановка чисел 1..n
получается из перестановки чисел 1..n-1 добавлением
числа n, которое можно вставить на любое из n мест.
При этом к сопоставляемой с ней последовательности
добавляется еще один член, принимающий значения от 0 до n-1, а предыдущие члены не меняются. При этом
оказывается, что изменение на единицу одного из членов
последовательности y соответствует транспозиции двух
соседних чисел, если все следующие числа
последовательности y принимают максимально или
минимально возможные для них значения. Именно, увеличение y[i] на 1 соответствует транспозиции числа i
с его правым соседом, а уменьшение - с левым.
. В нем
столько же элементов, сколько в множестве всех
перестановок, и мы сейчас установим между ними взаимно
однозначное соответствие. Именно, каждой перестановке
поставим в соответствие последовательность y[1]..y[n],
где y[i] - количество чисел, меньших i и стоящих
левее i в этой перестановке. Взаимная однозначность
вытекает из такого замечания. Перестановка чисел 1..n
получается из перестановки чисел 1..n-1 добавлением
числа n, которое можно вставить на любое из n мест.
При этом к сопоставляемой с ней последовательности
добавляется еще один член, принимающий значения от 0 до n-1, а предыдущие члены не меняются. При этом
оказывается, что изменение на единицу одного из членов
последовательности y соответствует транспозиции двух
соседних чисел, если все следующие числа
последовательности y принимают максимально или
минимально возможные для них значения. Именно, увеличение y[i] на 1 соответствует транспозиции числа i
с его правым соседом, а уменьшение - с левым.
Теперь вспомним решение задачи о перечислении всех последовательностей, на каждом шаге которого один член меняется на единицу. Заменив прямоугольную доску доской в форме лестницы (высота i -ой вертикали равна i ) и двигая шашки по тем же правилам, мы перечислим все последовательности y, причем i -ый член будет меняться как раз только если все следующие шашки стоят у края. Надо еще уметь параллельно с изменением y корректировать перестановку. Очевидный способ требует отыскания в ней числа i ; это можно облегчить, если помимо самой перестановки хранить функцию
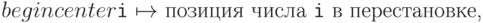
program test;
| const n=...;
| var
| x: array [1..n] of 1..n; {перестановка}
| inv_x: array [1..n] of 1..n; {обратная перестановка}
| y: array [1..n] of integer; {y[i] < i}
| d: array [1..n] of -1..1; {направления}
| b: boolean;
|
| procedure print_x;
| | var i: integer;
| begin
| | for i:=1 to n do begin
| | | write (x[i], ' ');
| | end;
| | writeln;
| end;
|
| procedure set_first;{первая: y[i]=0 при всех i}
| | var i : integer;
| begin
| | for i := 1 to n do begin
| | | x[i] := n + 1 - i;
| | | inv_x[i] := n + 1 - i;
| | | y[i]:=0;
| | | d[i]:=1;
| | end;
| end;
|
| procedure move (var done : boolean);
| | var i, j, pos1, pos2, val1, val2, tmp : integer;
| begin
| | i := n;
| | while (i > 1) and (((d[i]=1) and (y[i]=i-1)) or
| | | ((d[i]=-1) and (y[i]=0))) do begin
| | | i := i-1;
| | end;
| | done := (i>1); {упрощение: первый член нельзя менять}
| | if done then begin
| | | y[i] := y[i]+d[i];
| | | for j := i+1 to n do begin
| | | | d[j] := -d[j];
| | | end;
| | | pos1 := inv_x[i];
| | | val1 := i;
| | | pos2 := pos1 + d[i];
| | | val2 := x[pos2];
| | | {pos1, pos2 - номера переставляемых элементов;
| | | val1, val2 - их значения; val2 < val1}
| | | tmp := x[pos1];
| | | x[pos1] := x[pos2];
| | | x[pos2] := tmp;
| | | tmp := inv_x[val1];
| | | inv_x[val1] := inv_x[val2];
| | | inv_x[val2] := tmp;
| | end;
| end;
|
begin
| set_first;
| print_x;
| b := true;
| {напечатаны все перестановки до текущей включительно;
| если b ложно, то текущая - последняя}
| while b do begin
| | move (b);
| | if b then print_x;
| end;
end.



