Стохастические методы обучения нейронных сетей

Полезная стратегия для избежания подобных проблем состоит в больших начальных шагах и постепенном уменьшении размера среднего случайного шага. Это позволяет сети вырываться из локальных минимумов и в то же время гарантирует окончательную стабилизацию сети.

Ловушки локальных минимумов досаждают всем алгоритмам обучения, основанным на поиске минимума (включая персептрон и сети обратного распространения), и представляют серьезную и широко распространенную трудность, которую почему-то часто игнорируют. Стохастические методы позволяют решить эту проблему. Стратегия коррекции весов, вынуждающая веса принимать значение глобального оптимума в точке , вполне возможна.

В качестве объясняющей аналогии предположим, что на рис. 7.2 изображен шарик на поверхности внутри коробки. Если коробку сильно потрясти в горизонтальном направлении, то шарик будет быстро перекатываться от одного края к другому. Нигде не задерживаясь, в каждый момент времени шарик будет с равной вероятностью находиться в любой точке поверхности.

Если постепенно уменьшать силу встряхивания, то будет достигнуто условие, при котором шарик будет на короткое время "застревать" в точке 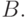При еще более слабом встряхивании шарик будет на короткое время останавливаться как в точке , так и в точке 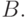При непрерывном уменьшении силы встряхивания будет достигнута критическая точка, когда сила встряхивания достаточна для перемещения шарика из точки в точку , но недостаточна для того, чтобы шарик мог "вскарабкаться" из в 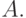Таким образом, окончательно шарик остановится в точке глобального минимума, когда амплитуда встряхивания уменьшится до нуля.

Искусственные нейронные сети могут обучаться, по существу, тем же способом при помощи случайной коррекции весов. Вначале делаются большие случайные коррекции с сохранением только тех изменений весов, которые уменьшают целевую функцию. Затем средний размер шага постепенно уменьшается, и глобальный минимум в конце концов достигается.

Эта процедура весьма напоминает отжиг металла, поэтому для ее описания часто используют термин "имитация отжига". В металле, который нагрет до температуры, превышающей его точку плавления, атомы находятся в сильном беспорядочном движении. Как и во всех физических системах, атомы стремятся к состоянию минимума энергии (единому кристаллу, в данном случае), но при высоких температурах энергия атомных движений препятствует этому. В процессе постепенного охлаждения металла возникают все более низкоэнергетические состояния, пока, в конце концов, не будет достигнуто самое малое из возможных состояний, глобальный минимум. В процессе отжига распределение энергетических уровней описывается следующим соотношением:

где — вероятность того, что система находится в состоянии с энергией ; — постоянная Больцмана; — температура по шкале Кельвина.

При высоких температурах приближается к единице для всех энергетических состояний. Таким образом, высокоэнергетическое состояние почти столь же вероятно, как и низкоэнергетическое. По мере уменьшения температуры вероятность высокоэнергетических состояний уменьшается по отношению к низкоэнергетическим. При приближении температуры к нулю становится весьма маловероятным, чтобы система находилась в высокоэнергетическом состоянии.