Персептроны. Обучение персептрона

Целочисленность весов персептронов

Для ответа на вопрос о количественных характеристиках вектора w рассмотрим следующую теорему.

Теорема. Любой персептрон можно заменить другим персептроном того же вида с целыми весами связей.

Доказательство.Обозначим множество примеров одного класса (правильный ответ равен 0) через , а другого (правильный ответ равен 1) — через 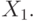Вычислим максимальное и минимальное значения суммы в правой части (1):

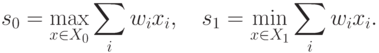
Определим допуск как минимум из и Положим 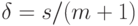, где — число слагаемых в (1). Поскольку персептрон (1) решает поставленную задачу классификации и множество примеров в обучающей выборке конечно, то Из теории чисел известна теорема о том, что любое действительное число можно сколь угодно точно приблизить рациональными числами. Заменим веса 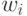на рациональные числа так, чтобы выполнялись следующие неравенства: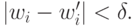

Из этих неравенств следует, что при использовании весов 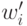персептрон будет работать с теми же результатами, что и первоначальный персептрон. Действительно, если правильным ответом примера является 0, имеем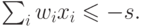

Подставив новые веса, получим:

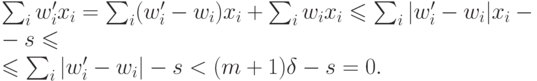
Откуда следует необходимое неравенство

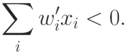( 2)

Аналогично, в случае правильного ответа равного 1, имеем , откуда, подставив новые веса и порог, получим:

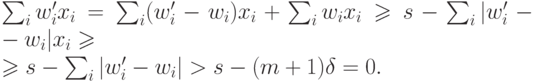
Отсюда следует выполнение неравенства

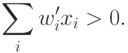( 3)

Неравенства (2) и (3) доказывают возможность замены всех весов и порога любого персептрона рациональными числами. Очевидно также, что при умножении всех весов и порога на одно и то же ненулевое число персептрон не изменится. Поскольку любое рациональное число можно представить в виде отношения целого числа к натуральному числу, получим

( 4)

где 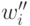— целые числа. Обозначим через произведение всех знаменателей: Умножим все веса и порог на 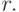Получим веса целочисленные 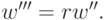Из (2), (3) и (4) получаем

что и завершает доказательство теоремы.

Поскольку из доказанной теоремы следует, что веса персептрона являются целыми числами, то вопрос о выборе шага при применении правил обучения решается просто: веса и порог следует увеличивать (уменьшать) на единицу.