| Россия, Липецк, Липецкий Государственный Технический Университет, 2014 |
Оптимизация и распараллеливание вычислительной программы на примере моделирования системы взаимодействующих частиц методом молекулярной динамики
Метод молекулярной динамики
Метод молекулярной динамики является одним из основных методов моделирования динамики систем, состоящих из взаимодействующих между собой частиц. Он применяется в молекулярной физике, астрофизике и других науках. Интерпретация понятия «частица» зависит от предметной области. В молекулярной физике это могут быть атом или молекула, а в астрофизике «частицами» являются звезды или планеты, взаимодействующие с другими астрономическими объектами посредством гравитационного взаимодействия. Динамика систем таких частиц часто описывается уравнениями классической механики.
Будем рассматривать систему  частиц, динамика которых описывается уравнением второго закона Ньютона:
частиц, динамика которых описывается уравнением второго закона Ньютона:
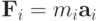
Здесь 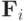 - равнодействующая всех сил, действующих на
- равнодействующая всех сил, действующих на  -ю частицу,
-ю частицу,  - ее масса и
- ее масса и  - ускорение, с которым частица двигается под действием силы. Это обыкновенное дифференциальное уравнение второго порядка, которое можно записать в виде:
- ускорение, с которым частица двигается под действием силы. Это обыкновенное дифференциальное уравнение второго порядка, которое можно записать в виде:

где 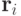 - радиус-вектор
- радиус-вектор  -й частицы.
-й частицы.
Равнодействующая сил, является суммой парных взаимодействий  -й частицы со всеми остальными частицами:
-й частицы со всеми остальными частицами:
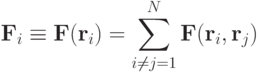
или
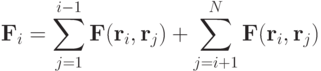
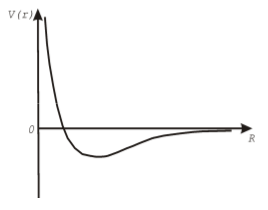
Сила взаимодействия связана с потенциалом взаимодействия. В расчетах молекулярных систем часто используют потенциал Леннарда-Джонса:
![V(r)=4\varepsilon\left[\left(\frac{\sigma}{r}\right)^{12}-\left(\frac{\sigma}{r}\right)^{6}\right]](/sites/default/files/tex_cache/35898dbc352d647d3a08ab6544949a9a.png)
Здесь 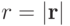 , а
, а  и
и  - параметры потенциала. Первый определяет интенсивность взаимодействия, а второй – положение минимума (см. рис. 1).
- параметры потенциала. Первый определяет интенсивность взаимодействия, а второй – положение минимума (см. рис. 1).
Потенциал Леннарда-Джонса хорошо описывает взаимодействие между атомами Аргона. Для аргона  ,
,  ,
, 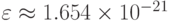 . Будем считать, что массы всех частиц одинаковы, система единиц выбрана таким образом, что
. Будем считать, что массы всех частиц одинаковы, система единиц выбрана таким образом, что 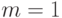 ,
, 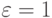 и
и 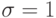 . Тогда сила парного взаимодействия:
. Тогда сила парного взаимодействия:
![\mathbf{F}(\mathbf{r}_i,\mathbf{r}_j) = \frac{24(\mathbf{r}_i-\mathbf{r}_j)}{\left|\mathbf{r}_i-\mathbf{r}_j\right|^2}\left[\frac{2}{\left|\mathbf{r}_i-\mathbf{r}_j\right|^{12}}-\frac{1}{\left|\mathbf{r}_i-\mathbf{r}_j\right|^6}\right]](/sites/default/files/tex_cache/ea1094b55e06e25bcb369952ba4d500b.png)
Интерес могут представлять траектории частиц или термодинамические характеристики системы, например, зависимость температуры от времени:
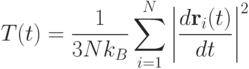
где  - постоянная Больцмана.
- постоянная Больцмана.
Для вычисления траекторий в методе молекулярной динамики используются различные алгоритмы. Они основаны на замене непрерывного времени дискретным набором значений 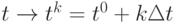 ,
, 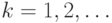 . Одним из алгоритмов является метод Верле:
. Одним из алгоритмов является метод Верле:
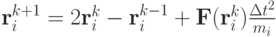
Здесь  . Наиболее трудоемким является вычисление силы, действующей на частицу.
. Наиболее трудоемким является вычисление силы, действующей на частицу.
Для оптимизации вычисления сил иногда вводится радиус обрезания – некоторый фиксированный (достаточно большой) радиус, такой, что пересчет сил, действующих между частицами, оказавшимися внутри этого радиуса, производится на каждом шаге. Пересчет сил, действующих со стороны более удаленных частиц, производится через несколько шагов. Такая стратегия позволяет уменьшить количество трудоемких операций расчета парных сил. Номера «ближайших» частиц могут храниться в специальном массиве. Такой массив называется списком. Обычно используются два массива целого типа. Каждый элемент первого массива (list_nb) содержит количество ближайших соседей соответствующей частицы:
k0 = 0
j0 = 0
do i = 1, n
do j =1, n
if(abs(x(i) – x(j)) < rcutoff) then
j0 = j0 + 1
list_nb(i) = j
end if
end do
i_nb(i) = j0 – k0
end do
Во втором массиве содержатся номера соседей каждой частицы. Положения хранятся в элементах, начиная с start(i) и заканчивая finish(i):
start(1) = 1
finish(1) = i_nb(1)
do i = 2, n
start(i) = finish(i – 1) + 1
finish(i) = finish(i – 1) + i_nb(i)
end do