|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Экономико-математические модели и принятие решений
Асимптотически оптимальный план. Из проведенных рассуждений ясно, что напряженный план с  является оптимальным тогда и только тогда, когда горизонт планирования Т приходится на начало очередного зубца, т.е. для
является оптимальным тогда и только тогда, когда горизонт планирования Т приходится на начало очередного зубца, т.е. для
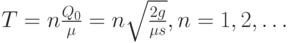 |
( 36) |
Для всех остальных возможных горизонтов планирования  этот план не является оптимальным. Оптимальным будет напряженный план с другим размером поставки. Для дальнейшего весьма существенно, что при изменении горизонта планирования
этот план не является оптимальным. Оптимальным будет напряженный план с другим размером поставки. Для дальнейшего весьма существенно, что при изменении горизонта планирования  от 0 до
от 0 до 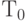 оптимальный план меняется на всем интервале
оптимальный план меняется на всем интервале ![[0; T_0]](/sites/default/files/tex_cache/a034696247ed539981c76e844e68a725.png) .
.
Как происходит это изменение? При малых горизонтах планирования  делается лишь одна поставка (в момент времени
делается лишь одна поставка (в момент времени  ), график уровня запаса на складе состоит из одного зубца. При увеличении
), график уровня запаса на складе состоит из одного зубца. При увеличении  размер зубца плавно увеличивается. В некоторый момент
размер зубца плавно увеличивается. В некоторый момент  происходит переход от одного зубца к двум. В этот момент оптимальны сразу два плана поставки - с одним зубцом и с двумя. При переходе к планам с двумя зубцами размер зубца скачком уменьшается. При дальнейшем увеличении горизонта планирования оптимальный план описывается графиком с двумя одинаковыми зубцами, размер которых плавно растет. Далее в момент
происходит переход от одного зубца к двум. В этот момент оптимальны сразу два плана поставки - с одним зубцом и с двумя. При переходе к планам с двумя зубцами размер зубца скачком уменьшается. При дальнейшем увеличении горизонта планирования оптимальный план описывается графиком с двумя одинаковыми зубцами, размер которых плавно растет. Далее в момент  становится оптимальным план с тремя зубцами, размер которых в этот момент скачком уменьшается (в компенсацию за увеличение числа скачков). И т.д.
становится оптимальным план с тремя зубцами, размер которых в этот момент скачком уменьшается (в компенсацию за увеличение числа скачков). И т.д.
Проблема состоит в том, что в реальной экономической ситуации выбор горизонта планирования Т весьма субъективен. Возникает вопрос, какой план разумно использовать, если горизонт планирования не известен заранее. Проблема горизонта планирования возникает не только в логистике. Она является общей для любого перспективного планирования, поэтому весьма важна для стратегического менеджмента. Для решения проблемы горизонта планирования необходимо использование конкретной модели принятия решений, в рассматриваемом случае - классической модели управления запасами.
Ответ можно указать, если горизонт планирования является достаточно большим. Оказывается можно использовать план, в котором все размеры поставок равны 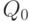 . Для него уровень запаса на складе описывается функцией
. Для него уровень запаса на складе описывается функцией 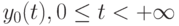 , состоящей из зубцов высоты
, состоящей из зубцов высоты 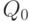 . Предлагается пользоваться планом, являющимся сужением этого плана на интервал
. Предлагается пользоваться планом, являющимся сужением этого плана на интервал 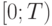 . Другими словами, предлагается на интервале
. Другими словами, предлагается на интервале 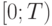 использовать начальный отрезок этого плана. Он состоит из некоторого количества треугольных зубцов, а последний участок графика, описываемый трапецией, соответствует тому, что последняя поставка для почти всех горизонтов планирования не будет израсходована до конца. Такой план иногда называют планом Вильсона .
использовать начальный отрезок этого плана. Он состоит из некоторого количества треугольных зубцов, а последний участок графика, описываемый трапецией, соответствует тому, что последняя поставка для почти всех горизонтов планирования не будет израсходована до конца. Такой план иногда называют планом Вильсона .
Ясно, что этот план не будет оптимальным (для всех  , кроме заданных формулой (36)). Действительно, план Вильсона можно улучшить, уменьшив объем последней поставки. Однако у него есть то полезное качество, что при изменении горизонта планирования его начальный отрезок не меняется. Действительно, планы поставок для горизонтов планирования
, кроме заданных формулой (36)). Действительно, план Вильсона можно улучшить, уменьшив объем последней поставки. Однако у него есть то полезное качество, что при изменении горизонта планирования его начальный отрезок не меняется. Действительно, планы поставок для горизонтов планирования 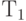 и
и  , определенные с помощью функции
, определенные с помощью функции  , задающей уровень запасов на складе, совпадают на интервале
, задающей уровень запасов на складе, совпадают на интервале  .
.
Определение. Асимптотически оптимальным планом называется план поставок - функция  такая, что
такая, что
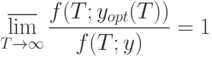
где 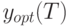 - оптимальный план на интервале
- оптимальный план на интервале 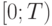 .
.
В соответствии с определениями и обозначениями, введенными в начале раздела, 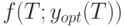 - средние издержки за время
- средние издержки за время  для плана
для плана 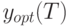 , определенного на интервале
, определенного на интервале 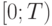 , а
, а 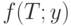 - средние издержки за время
- средние издержки за время  для плана
для плана 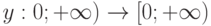 .
.
Теорема 1. План y = y0 является асимптотически оптимальным.
Таким образом, для достаточно больших горизонтов планирования  планы
планы  , все зубцы у которых имеют высоту
, все зубцы у которых имеют высоту 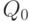 , имеют издержки, приближающиеся к минимальным. Следовательно, эти планы Вильсона, являющиеся сужениями одной и той же функции
, имеют издержки, приближающиеся к минимальным. Следовательно, эти планы Вильсона, являющиеся сужениями одной и той же функции  на интервалы
на интервалы 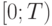 при различных
при различных  , можно использовать одновременно при всех достаточно больших
, можно использовать одновременно при всех достаточно больших  .
.
Замечание.Pешение проблемы горизонта планирования состоит в использовании асимптотически оптимальных планов, которые близки (по издержкам) к оптимальным планам сразу при всех достаточно больших  .
.
Доказательство. По определению оптимального плана
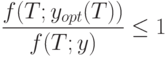 |
( 37) |
Найдем нижнюю границу для рассматриваемого отношения. При фиксированном  можно указать неотрицательное целое число n такое, что
можно указать неотрицательное целое число n такое, что
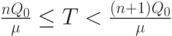
Так как 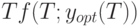 и
и 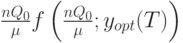 - общие издержки на интервалах
- общие издержки на интервалах 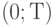 и
и  соответственно при использовании оптимального на
соответственно при использовании оптимального на 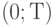 плана, то, очевидно, поскольку второй интервала - часть первого (или совпадает с ним), первые издержки больше вторых, т.е.
плана, то, очевидно, поскольку второй интервала - часть первого (или совпадает с ним), первые издержки больше вторых, т.е.

Далее, т.к. на интервале  , включающем целое число периодов плана
, включающем целое число периодов плана  , оптимальным является начальный отрезок этого плана
, оптимальным является начальный отрезок этого плана 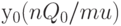 , то
, то
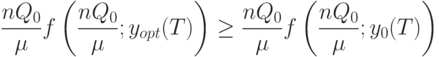
В правой части последнего неравенства стоит  (здесь использована формула для минимального значения средних издержек
(здесь использована формула для минимального значения средних издержек 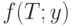 при
при  , кратном
, кратном 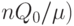 . Из проведенных рассуждений вытекает, что
. Из проведенных рассуждений вытекает, что
 |
( 38) |
Для общих издержек на интервалах 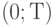 и
и 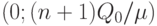 при использовании плана
при использовании плана 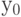 , очевидно, справедливо следующее неравенство
, очевидно, справедливо следующее неравенство
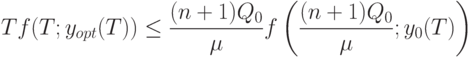
Следовательно,
 |
( 39) |
Из неравенств (38) и (39) вытекает, что
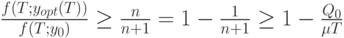
Так как  при
при  , то, учитывая неравенство (37), из последнего неравенства выводим справедливость заключения теоремы 1. Таким образом, асимптотическая оптимальность плана
, то, учитывая неравенство (37), из последнего неравенства выводим справедливость заключения теоремы 1. Таким образом, асимптотическая оптимальность плана 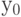 доказана.
доказана.
При небольшом  средние издержки в плане Вильсона могут существенно превышать средние издержки в оптимальном плане. Превышение вызвано скачками функции
средние издержки в плане Вильсона могут существенно превышать средние издержки в оптимальном плане. Превышение вызвано скачками функции 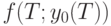 , связанными с переходами через моменты прихода очередных поставок (и увеличением общих издержек скачком на величину платы за доставку партии). Величину превышения средних издержек в плане Вильсона по сравнению с оптимальными планами можно рассчитать.
, связанными с переходами через моменты прихода очередных поставок (и увеличением общих издержек скачком на величину платы за доставку партии). Величину превышения средних издержек в плане Вильсона по сравнению с оптимальными планами можно рассчитать.
Пусть горизонт планирования  , где
, где 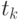 - момент прихода
- момент прихода 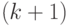 -й поставки в плане Вильсона,
-й поставки в плане Вильсона, 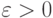 . Тогда, как можно доказать,
. Тогда, как можно доказать,
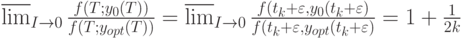
Таким образом, затраты в плане Вильсона являются минимальными (относительно оптимального плана) при  где
где 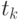 - моменты прихода поставок. Напомним, что план Вильсона является оптимальным при указанных
- моменты прихода поставок. Напомним, что план Вильсона является оптимальным при указанных  . Однако при
. Однако при  , бесконечно близком к
, бесконечно близком к 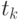 , но превосходящем
, но превосходящем 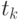 , затраты увеличиваются по сравнению с затратами в оптимальном плане в
, затраты увеличиваются по сравнению с затратами в оптимальном плане в 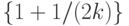 раз. При дальнейшем возрастании Т отношение издержек (средних или общих) в плане Вильсона к аналогичным издержкам в оптимальном плане постепенно уменьшается, приближаясь к 1 при приближении (снизу) к моменту
раз. При дальнейшем возрастании Т отношение издержек (средних или общих) в плане Вильсона к аналогичным издержкам в оптимальном плане постепенно уменьшается, приближаясь к 1 при приближении (снизу) к моменту 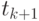 прихода следующей поставки. А там - новый скачок, но уже на меньшую величину
прихода следующей поставки. А там - новый скачок, но уже на меньшую величину  . И т.д.
. И т.д.
Сразу после прихода первой поставки отношение затрат составляет 1,5 (превышение на 50%), после прихода второй - 1,25 (превышение на 25%), третьей - 1,167 (превышение на 16,7%), четвертой - 1,125 (превышение на 12,5%), пятой - 1,1 (превышение на 10%), и т.д. Таким образом, при небольших горизонтах планирования Т превышение затрат может быть значительным, план Вильсона отнюдь не оптимальный. Но чем больше горизонт планирования, тем отклонение меньше. Уже после сотой поставки оно не превышает 0,5%.
Влияние отклонений от оптимального объема партии. В реальных производственных и управленческих ситуациях часто приходится принимать решения об использовании объемов партии, отличных от оптимальной величины 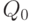 , рассчитанной по формуле квадратного корня (34). Например, при ограниченной емкости склада или для обеспечения полной загрузки транспортных средств большой вместимости. Это возможно также в ситуации, когда величина партии измеряется в целых числах (штучный товар) или даже в десятках, дюжинах, упаковках, ящиках, контейнерах и т.д., а величина
, рассчитанной по формуле квадратного корня (34). Например, при ограниченной емкости склада или для обеспечения полной загрузки транспортных средств большой вместимости. Это возможно также в ситуации, когда величина партии измеряется в целых числах (штучный товар) или даже в десятках, дюжинах, упаковках, ящиках, контейнерах и т.д., а величина 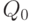 не удовлетворяет этому требованию и, следовательно, не может быть непосредственно использована в качестве объема поставки.
не удовлетворяет этому требованию и, следовательно, не может быть непосредственно использована в качестве объема поставки.
Поэтому необходимо уметь вычислять возрастание средних издержек при использовании напряженного плана с одинаковыми поставками объема  , отличного от
, отличного от 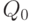 , по сравнению со средними издержками в оптимальном плане. Будем сравнивать средние издержки за целое число периодов. Как показано выше, они имеют вид
, по сравнению со средними издержками в оптимальном плане. Будем сравнивать средние издержки за целое число периодов. Как показано выше, они имеют вид

где  - объем партии. Тогда
- объем партии. Тогда
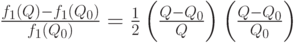 |
( 40) |
Это тождество нетрудно проверить с помощью простых алгебраических преобразований.
Пример 2. Пусть используется план с 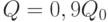 . Тогда
. Тогда

Таким образом, изменение объема партии на 10% привело к увеличению средних издержек лишь на 0,56%.
Пример 3. Пусть используемое значение объема поставки  отличается от оптимального не более чем на 30%. На сколько могут возрасти издержки?
отличается от оптимального не более чем на 30%. На сколько могут возрасти издержки?
Из формулы (40) вытекает, что максимальное возрастание издержек будет в случае 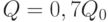 . Тогда
. Тогда
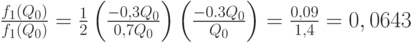
Таким образом, издержки могут возрасти самое большее на 6,43%.
На первый взгляд представляется удивительным, что сравнительно большое отклонение значения переменной  от оптимального (на 30%) приводит к столь малому возрастанию значения оптимизируемой функции. Этот факт имеет большое прикладное значение. Из него следует, что область "почти оптимальных" значений параметра весьма обширна, следовательно, из нее можно выбирать для практического использования те или иные значения, исходя из иных принципов. Можно, например, минимизировать какую-либо иную целевую функцию, тем самым, решая задачу многокритериальной оптимизации. Можно "вписаться" в действующую дискретную систему возможных значений параметров. И т.д.
от оптимального (на 30%) приводит к столь малому возрастанию значения оптимизируемой функции. Этот факт имеет большое прикладное значение. Из него следует, что область "почти оптимальных" значений параметра весьма обширна, следовательно, из нее можно выбирать для практического использования те или иные значения, исходя из иных принципов. Можно, например, минимизировать какую-либо иную целевую функцию, тем самым, решая задачу многокритериальной оптимизации. Можно "вписаться" в действующую дискретную систему возможных значений параметров. И т.д.
Важное замечание 1. Обширность области "почти оптимальных" значений параметра - общее свойство оптимальных решений, получаемых путем минимизации гладких функций. Действительно, пусть необходимо минимизировать некоторую функцию 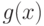 , трижды дифференцируемую. Пусть минимум достигается в точке
, трижды дифференцируемую. Пусть минимум достигается в точке 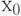 . Справедливо разложение Тейлора-Маклорена
. Справедливо разложение Тейлора-Маклорена
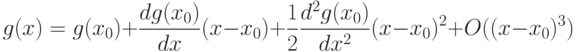
Однако в х0 выполнено необходимое условие экстремума (в данном случае - минимума)
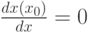
Следовательно, с точностью до бесконечно малых более высокого порядка (по сравнению с  ) справедливо равенство
) справедливо равенство
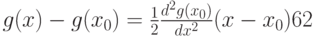 |
( 41) |
Это соотношение показывает, что приращение значений минимизируемой функции - бесконечно малая более высокого порядка по сравнению с приращением независимой переменной. Если
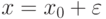
то
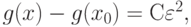
где
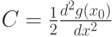
Вернемся к классической модели управления запасами. Для нее надо рассматривать 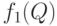 в роли
в роли 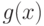 . С помощью соотношения (41) заключаем, что
. С помощью соотношения (41) заключаем, что

с точностью до бесконечно малых более высокого порядка. Вычислим вторую производную 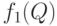 . Поскольку
. Поскольку

то
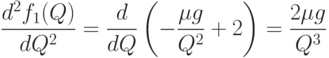
Теперь заметим, что
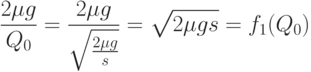
Следовательно,
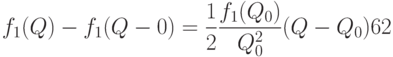
с точностью до бесконечно малых более высокого порядка. Отличие этой формулы от точной формулы (40) состоит только в том, что  в знаменателе одной из дробей заменено на
в знаменателе одной из дробей заменено на 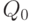 .
.
