|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Вероятностно-статистические методы принятия решений
Следующий этап - разработка методологии применения различных методов управления рисками с использованием экспертных оценок, эконометрических и экономико-математических моделей с целью повышения эффективности деятельности организации в условиях риска. При этом необходимо научиться практически решать проблему многокритериальности (согласования оценок рисков, полученных по различным основаниям, с целью эффективного управления риском).
Производственные риски.К ним следует, прежде всего, отнести риски, связанные с выпуском дефектной продукции. Хорошо известно, что при массовом производстве невозможно обеспечить выпуск продукции без дефектов. Поэтому действуют отделы технического контроля (ОТК), службы (бюро) качества и другие подразделения, осуществляющие контроль качества продукции. Известно, что в машиностроении стоимость контрольных операций составляет в среднем около 10% от стоимости продукции. Часть риска компенсируется службами технического обслуживания продукции, уже находящейся у потребителя. Постоянно используемыми терминами в этой области являются "риск поставщика" и "риск потребителя".
Другой вид рисков связан с осуществлением действующих технологических процессов. Речь идет об авариях различной степени тяжести, от незначительных нарушений технологических процессов до катастроф с человеческими жертвами. Здесь целесообразно обратить внимание на экологические риски, в частности, связанные с аварийными сбросами в реки технологических жидкостей, выбросами в атмосферу газов и взвешенных частиц и др. За подобные действия предприятия обычно обязаны платить штрафы согласно предписаниям экологических органов.
Отметим риски, относящиеся к проектируемой продукции или технологическим процессам. Они могут быть связаны с ошибками разработчиков или физической невозможностью осуществления того или иного процесса. Так, в течение всей второй половины ХХ века физики постоянно говорили о появлении в ближайшее время неиссякаемого источника энергии на основе преобразования тяжелой воды с помощью управляемого термоядерного синтеза.
Среди производственных рисков есть и социальные, связанные с теми или иными конфликтами. Здесь надо выделить конфликты между службами (отделами, цехами), с которыми можно бороться, оптимизируя организационную структуру предприятия. Далее - различного происхождения конфликты между менеджерами высшего звена; конфликты между профсоюзами и администрацией по поводу заработной платы или условий труда, и др. Современные методы управления персоналом позволяют заранее спрогнозировать многие из таких конфликтов и предложить пути их разрешения.
Коммерческие риски.Речь идет о рисках, связанных с неопределенностью будущей рыночной ситуации в стране. В частности, о будущих действиях поставщиков в связи с меняющимися предпочтениями потребителей. Напомним, например, о быстрых изменениях на рынке вычислительной техники в связи с появлением персональных компьютеров. Мода в той или иной степени отражается на поведении потребителей во многих областях.
Весьма существенны риски, связанные с деятельностью партнеров организации - участников экономической жизни, в частности, с их деловой активностью, финансовым положением, отношением к соблюдению обязательств. Отметим роль конкурентного окружения, от действий которого зависит многое в судьбе предприятия. В частности, важны информационные риски, связанные с промышленным шпионажем.
Существенны риски, связанные с социальными и административными факторами в конкретных регионах, с взаимоотношениями рассматриваемой организации с органами местной и региональной власти как официальными, так и криминальными.
Финансовые риски.Отметим, прежде всего, риски, связанные с колебаниями цен на товары и услуги (динамикой инфляции), ставки рефинансирования Центрального банка, норм банковских процентов по кредитам и депозитам, валютных курсов и других макроэкономических показателей, в том числе котировок государственных и частных (корпоративных) ценных бумаг. Часть этих рисков носит объективный, а часть - чисто спекулятивный характер. К этому же разделу можно отнести риски, связанные с нестабильностью законодательства и текущей экономической политики (т.е. с деятельностью руководства страны, министерств и ведомств). Дополнительные проблемы создает множественность нормативно-правовых актов, регулирующих хозяйственно-экономическую деятельность организации, зачастую противоречащих друг другу, что вызывает необходимость участия юристов в работе организации.
Риски, возникающие на уровне государства и Земли в целом. К этому типу отнесем риски, связанные с политической ситуацией в целом, действиями партий, профсоюзов, экологических и других организаций в масштабе страны. Типичным примером являются риски, связанные с заметным изменением курса страны в результате тех или иных выборов. Другой пример - российский кризис, начавшийся в августе 1998 г. Большое значение имеют риски, связанные с социальной борьбой ("рельсовая война", забастовки, массовые столкновения, терроризм, и др.)…
Внешнеэкономические риски, например, связанные с динамикой цен на нефть, крупномасштабными финансовыми (в Юго-Восточной Азии) или военными (Югославия, Ирак) кризисами, могут оказать существенное воздействие на организацию.
Большое число рисков связано с природными явлениями. Их можно объединить под именем "экологические". Типичным примером является погода, от которой зависят урожайность (а потому и цены на сельскохозяйственные товары), расходы на отопление и уборку улиц, доходы от туризма и др. Есть риски, связанные с недостаточными знаниями о природе. Например, неизвестен точный объем полезных ископаемых в том или ином месторождении, а потому нельзя точно предсказать развитие добывающей промышленности и объем налоговых поступлений от ее предприятий. Вспомним и о рисках экологических бедствий и катастроф, типа ураганов, смерчей, землетрясений, цунами, селей.
Каждый из перечисленных видов рисков может быть структурирован далее. Так, имеются крупные развернутые разработки по анализу рисков технологических аварий, в частности, на химических производствах и на атомных электростанциях. Ясно, что аварии типа Чернобыльской существенно влияют на значения СТЭЭП-факторов и тем самым на поступления и выплаты из бюджета как на местном, так и на федеральном уровне.
Подходы к учету неопределенности при описании рисков. В теории принятия решений для описания неопределенностей и рисков чаще всего используют такие математические средства, как:
- вероятностно-статистические методы,
- методы статистики нечисловых данных, в том числе интервальной статистики и интервальной математики, а также методы теории нечеткости,
- методы теории конфликтов (теории игр).
Они применяются в имитационных, эконометрических, экономико-математических моделях, реализованных обычно в виде программных продуктов.
Некоторые виды неопределенностей связаны с безразличными к организации силами - природными (погодные условия) или общественными (смена правительства). Если явление достаточно часто повторяется, то его естественно описывать в вероятностных терминах. Так, прогноз урожайности зерновых вполне естественно вести в вероятностных терминах.
Если событие единично, то вероятностное описание вызывает внутренний протест, поскольку частотная интерпретация вероятности невозможна. Так, для описания неопределенности, связанной с исходами выборов или со сменой правительства, лучше использовать методы теории нечеткости, в частности, интервальной математики.
Наконец, если неопределенность связана с активными действиями соперников или партнеров, целесообразно применять методы анализа конфликтных ситуаций, т.е. методы теории игр, прежде всего антагонистических игр, но иногда полезны и более новые методы кооперативных игр, нацеленных на получение устойчивого компромисса.
Подходы к оцениванию рисков.Понятие "риск", как уже отмечалось, многогранно.
Например, при использовании статистических методов управления качеством продукции риски - это вероятности некоторых событий (в статистическом приемочном контроле риск поставщика - это вероятность забракования партии продукции хорошего качества, а риск потребителя - вероятность приемки "плохой" партии; при статистическом регулировании процессов рассматривают риск незамеченной разладки и риск излишней наладки). Тогда оценка риска - это оценка вероятности, точечная или интервальная, по статистическим данным или экспертная. В таком случае для управления риском задают ограничения на вероятности нежелательных событий.
Иногда под уменьшением риска понимают уменьшение дисперсии случайной величины, описывающей ущерб, поскольку при этом уменьшается неопределенность. В теории принятия статистических решений риск - это плата за принятие решения, отличного от оптимального, он обычно выражается как математическое ожидание. В экономике плата измеряется обычно в денежных единицах, т.е. в виде финансового потока (потока платежей и поступлений) в условиях неопределенности.
Чтобы продемонстрировать сложность проблемы оценивания риска и различные существующие подходы, рассмотрим простейший случай. Пусть неопределенность носит вероятностный характер, а потери описываются одномерной случайной величиной (а не случайным вектором и не случайным процессом). Другими словами, ущерб адекватно описывается одним числом, а величина этого числа зависит от случая.
Итак, пусть величина порожденного риском ущерба моделируется неотрицательной случайной величиной 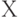 (в смысле теории вероятностей). Рассмотрим ее функцию распределения
(в смысле теории вероятностей). Рассмотрим ее функцию распределения
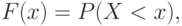
где 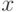 - действительное число. В зависимости от предположений о свойствах функции распределения
- действительное число. В зависимости от предположений о свойствах функции распределения  вероятностные модели риска делятся на параметрические и непараметрические.
вероятностные модели риска делятся на параметрические и непараметрические.
В первом случае предполагается, что функция распределения входит в одно из известных семейств распределений - нормальных (т.е. гауссовских), экспоненциальных или иных. Однако обычно подобное предположение является мало обоснованным - реальные данные не хотят "втискиваться" в заранее заданное семейство. Тогда необходимо применять непараметрические статистические методы, не предполагающие, что распределение ущерба взято из того или иного семейства.
Обсудим два распространенных заблуждения.
Во-первых, часто говорят, что поскольку величина ущерба зависит от многих причин, то она должна иметь т.н. нормальное распределение. Это неверно. Все зависит от способа взаимодействия причин. Если причины действуют аддитивно (эффекты складываются), то, действительно, в силу Центральной Предельной Теоремы теории вероятностей есть основания использовать нормальное (гауссово) распределение. Если же причины действуют мультипликативно (эффекты перемножаются), то в силу той же теоремы следует приближать распределение величины ущерба Х с помощью логарифмически нормального распределения Если же основное влияние оказывает "слабое звено" (где тонко, там и рвется), то согласно теоремам, доказанным академиком Б.В. Гнеденко, следует приближать распределение величины ущерба Х с помощью распределения из семейства Вейбулла-Гнеденко. К сожалению, в конкретных практических случаях различить эти варианты обычно не удается.
Во-вторых, неверно традиционное представление о том, что погрешности измерений нормально распределены. Проведенный многими специалистами тщательный анализ погрешностей реальных наблюдений показал, что их распределение в подавляющем большинстве случаев отличается от гауссова. Сводка этих исследований приведена в работе. Среди специалистов распространено такое шуточное утверждение: "Прикладники обычно думают, что математики доказали, что погрешности распределены нормально, а математики считают, что прикладники установили это экспериментально" . И те, и другие ошибаются. Причины появления ошибок разнообразны.
Итак, величина ущерба, связанного с риском, описывается функцией распределения 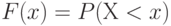 . Обычно стараются перейти от функции, описываемой бесконечно большим числом параметров, к небольшому числу числовых параметров, лучше всего к одному. Для положительной случайной величины (величины ущерба) часто рассматривают такие ее характеристики, как
. Обычно стараются перейти от функции, описываемой бесконечно большим числом параметров, к небольшому числу числовых параметров, лучше всего к одному. Для положительной случайной величины (величины ущерба) часто рассматривают такие ее характеристики, как
- математическое ожидание;
- медиана и, более общо, квантили (значение
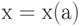 квантили порядка а находят из уравнения
квантили порядка а находят из уравнения 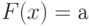 );
); - дисперсия (часто обозначаемая как "сигма-квадрат");
- среднее квадратическое отклонение (квадратный корень из дисперсии, т.е. "сигма");
- коэффициент вариации (среднее квадратическое отклонение, деленное на математическое ожидание);
- линейная комбинация математического ожидания и среднего квадратического отклонения (например, типично желание считать, что возможные значения ущерба расположены в таком интервале: математическое ожидание плюс-минус три сигма) ;
- математическое ожидание функции потерь, и т.д.
Этот перечень, очевидно, может быть продолжен.
Тогда задача оценки ущерба может пониматься как задача оценки той или иной из перечисленных характеристик. Чаще всего оценку проводят по эмпирическим данным (по выборке величин ущербов, соответствующим происшедшим ранее аналогичным случаям). При отсутствии эмпирического материала остается опираться на экспертные оценки. Наиболее обоснованным является модельно-расчетный метод, опирающийся на модели технологической, управленческой, экономической, социально-психологической, эколого-экономической ситуации.
Подчеркнем здесь, что характеристик случайного ущерба имеется много. Выше перечислено 7 видов, причем некоторые из них - второй, шестой и седьмой - содержат бесконечно много конкретных характеристик. Нельзя ограничиваться только средним ущербом, под которым обычно понимают математическое ожидание, хотя медиана ущерба не меньше соответствует этому термину. Весьма важны верхние границы для ущерба, т.е. квантили порядка а, где а близко к 1, например, а = 0,999999. При этом с вероятностью, не превосходящей 0,000001, реальный ущерб будет меньше х(0,999999).
Тогда минимизация риска может, например, состоять:
- в минимизации математического ожидания (ожидаемых потерь),
- в минимизации квантили распределения (например, медианы функции распределения потерь или квантили порядка 0,99, выше которой располагаются большие потери, встречающиеся редко - в 1 случае из 100),
- в минимизации дисперсии (т.е. показателя разброса возможных значений потерь),
- в минимизации суммы математического ожидания и утроенного среднего квадратического отклонения (на основе известного "правила трех сигм"), или иной линейной комбинации математического ожидания и среднего квадратического отклонения (используют в случае близости распределения потерь к нормальному как комбинацию подходов, нацеленных на минимизацию средних потерь и разброса возможных значений потерь),
- в минимизации математического ожидания функции потерь.
Перечень может быть продолжен. Например, не использована такая характеристика случайного ущерба, как коэффициент вариации.
Обсудим пять перечисленных постановок. Первая из них - минимизация средних потерь - представляется вполне естественной, если все возможные потери малы по сравнению с ресурсами предприятия. В противном случае первый подход использовать нецелесообразно. Рассмотрим условный пример. У человека имеется 10000 рублей. Ему предлагается подбросить монету. Если выпадает "орел", то он получает 50000 рублей. Если же выпадает "цифра", он должен уплатить 20000 рублей. Стоит ли данному человеку участвовать в описанном пари? Математическое ожидание дохода равно  руб. Казалось бы, пари весьма выгодно. Однако большинство людей на него не пойдет, поскольку с вероятностью 0,5 они лишатся всего своего достояния и останутся должны 10000 рублей, другими словами, разорятся. Здесь проявляется психологическая оценка ценности рубля, зависящая от общей имеющейся суммы - 10000 рублей для человека с обычным доходом значит гораздо больше, чем те же 10000 р
уб. для миллиардера.
руб. Казалось бы, пари весьма выгодно. Однако большинство людей на него не пойдет, поскольку с вероятностью 0,5 они лишатся всего своего достояния и останутся должны 10000 рублей, другими словами, разорятся. Здесь проявляется психологическая оценка ценности рубля, зависящая от общей имеющейся суммы - 10000 рублей для человека с обычным доходом значит гораздо больше, чем те же 10000 р
уб. для миллиардера.
Второй подход нацелен как раз на минимизацию больших потерь, на защиту от разорения. Другое его применение - исключение катастрофических аварий, например, типа Чернобыльской. При втором подходе средние потери могут увеличиться (по сравнению с первым), зато максимальные будут контролироваться.

