| Россия, Москва |
Контрастирование (редукция) нейронной сети
Опишем вычисления более детально.
1. Проводим нормировку: для любого  полагаем
полагаем 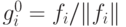 .
.
2. Вычисляем 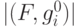 (модуль проекции вектора
(модуль проекции вектора  на вектор
на вектор 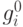 ),
), 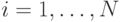 . Находим среди этих чисел максимальное (пусть его номер
. Находим среди этих чисел максимальное (пусть его номер  ),
полагаем
),
полагаем 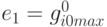 , исключаем
, исключаем  из множества
из множества 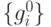 , получаем
, получаем 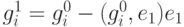 , исключаем из множества
, исключаем из множества 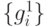 нулевые векторы, если
таковые существуют, проводим нормировку
нулевые векторы, если
таковые существуют, проводим нормировку 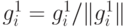 .
.
3. Пусть определены векторы 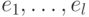 и не более чем
и не более чем 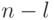 нормированных
векторов
нормированных
векторов 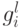 . Среди векторов
. Среди векторов 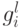 ищем такой
ищем такой 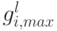 , для которого
, для которого 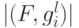 принимает максимальное значение, полагаем
принимает максимальное значение, полагаем 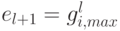 , исключаем
, исключаем 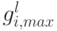 из множества векторов
из множества векторов 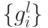 ;
полагаем
;
полагаем 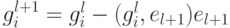 , исключаем из этого множества нулевые векторы,
если таковые
существуют, нормируем:
, исключаем из этого множества нулевые векторы,
если таковые
существуют, нормируем: 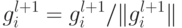 .
.
Вычисления проводим, пока  .
.
После завершения вычислений имеем набор ортонормированных векторов  . Они являются линейными комбинациями
векторов
. Они являются линейными комбинациями
векторов  . Коэффициенты разложения
. Коэффициенты разложения 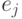 по набору
по набору  могут
быть вычислены и сохранены в ходе ортогонализации. Полагаем
могут
быть вычислены и сохранены в ходе ортогонализации. Полагаем 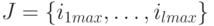 .
Тогда
.
Тогда  .
Это и есть решение
задачи. Числа
.
Это и есть решение
задачи. Числа 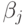 выражаются через коэффициенты разложения
векторов
выражаются через коэффициенты разложения
векторов 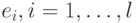 по
по 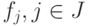 и скалярные произведения
и скалярные произведения 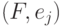 : если
: если  ,
то
,
то  .
.
Разложение 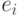 по
по  имеет рекурсивную
форму:
имеет рекурсивную
форму:
![\begin{align*}
&e_1 = f_{i,1max}/\|f_{i,1max}\|,\\
&e_2 = [f_{i,2max} - (f_{i,2max}, e_1)e1]/\|f_{i,2max} - (f_{i,2max},e_1)e_1\|,\\
&\ldots,\\
&e_j = [f_{i,jmax} - \sum_{r=1,j-1}(f_{i,jmax},e_r)e_r]/\| f_{i,jmax} -\sum_{r=1,j-1}(f_{i,jmax},e_r)e_r\|,\\
&\ldots
\end{align*}](/sites/default/files/tex_cache/5ba4a18cac450138f9fe975331b45917.png)
Для функций вида 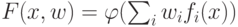 с
дифференцируемой функцией
процедура аналогична с точностью до замены скалярного произведения:
используется скалярное произведение с весами
с
дифференцируемой функцией
процедура аналогична с точностью до замены скалярного произведения:
используется скалярное произведение с весами 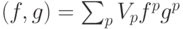 , где
, где  . В этом скалярном произведении вычисляются все
нормы и
проводится ортогонализация.
. В этом скалярном произведении вычисляются все
нормы и
проводится ортогонализация.
Для функций с пороговой нелинейностью на выходе используем скалярное
произведение с весами 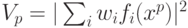 .
.
Описанная процедура сокращения "сверху вниз" с ортогонализацией особенно важна для упрощения элементов сложных сетей, в структуре которых и вектор входных сигналов элемента может быть далек от исходных данных, и его выходной сигнал далек от оцениваемого выхода всей сложной системы.
Процедуры анализа значимости и сокращения описания выделяют наиболее важные параметры и связи в НС. По аналогии с обработкой изображения их называют процедурами контрастирования или редукции.
Роль контрастирования (редукции) не сводится только к сокращению описания: более общая задача - привести параметры системы к выделенному набору значений, в частности, уменьшить разрядность, что важно для удешевления специализированных устройств, экономии памяти и т.д.
