|
Упражнение 2.1.25 |
Алгоритмически разрешимые проблемы
15.9*. Проблема неравенства регулярных выражений без итерации
Теорема 15.9.1. Проблема неравенства регулярных выражений без итерации ( то есть регулярных выражений с нулевой звездной высотой ) NP- полна.
Доказательство. По регулярному выражению без итерации легко построить конечный автомат с однобуквенными переходами, не содержащий циклов. Проблема неравенства таких конечных автоматов принадлежит классу NP: достаточно "угадать" слово, принадлежащее разности языков, распознаваемых двумя данными автоматами, и, продвигаясь по этому слову буква за буквой, подобно доказательству теоремы 2.7.1 вычислять, в каких состояниях автоматы могут оказаться. При этом длину слова можно ограничить максимумом числа состояний двух автоматов.
Осталось доказать, что проблема неравенства регулярных выражений без итерации NP-сложна. Для этого достаточно продемонстрировать, что к этой проблеме полиномиально сводится проблема выполнимости булевых формул в конъюнктивной нормальной форме (то есть множество кодов выполнимых булевых формул в конъюнктивной нормальной форме полиномиально сводится к множеству кодов пар неравных регулярных выражений без итерации). Искомое полиномиальное сведЕние может быть построено следующим образом.
Пусть дана
булева формула 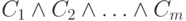 ,
составленная из пропозициональных переменных x1, x2, ..., xn
(при более формальном подходе можно считать xi обозначением слова p#i,
как это сделано в примере 7.2.8).
Здесь для каждого
,
составленная из пропозициональных переменных x1, x2, ..., xn
(при более формальном подходе можно считать xi обозначением слова p#i,
как это сделано в примере 7.2.8).
Здесь для каждого  формула Cj
является элементарной дизъюнкцией.
Для краткости будем обозначать отрицание переменной xi
через
формула Cj
является элементарной дизъюнкцией.
Для краткости будем обозначать отрицание переменной xi
через 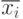 (а не через
(а не через  ,
как в примере 7.2.8).
,
как в примере 7.2.8).
Построим два регулярных выражения над алфавитом 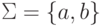 .
В качестве первого
регулярного выражения
возьмем
.
В качестве первого
регулярного выражения
возьмем
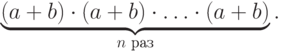
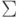 .
Второе
регулярное выражение e
построим так, чтобы выполнялось равенство
.
Второе
регулярное выражение e
построим так, чтобы выполнялось равенство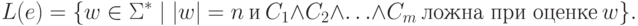
- если данная элементарная дизъюнкция не содержит
ни литерала xi,
ни литерала
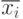 ,
то используем выражение (a+b) ;
,
то используем выражение (a+b) ; - если она
содержит
литерал xi,
но не содержит
литерала
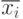 ,
то используем выражение a ;
,
то используем выражение a ; - если она содержит
литерал
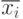 ,
но не содержит
литерала xi,
то используем выражение b ;
,
но не содержит
литерала xi,
то используем выражение b ; - если она содержит оба литерала xi и
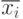 ,
то используем выражение 0.
,
то используем выражение 0.
Если m > 1, то построим по указанному методу для каждой из булевых формул C1, C2, ..., Cm регулярное выражение и возьмем их сумму.
Легко видеть, что
два построенных так регулярных выражения равны тогда и только тогда,
когда
булева формула 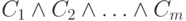 невыполнима.
невыполнима.
Пример 15.9.2.
Пусть 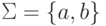 .
Регулярные выражения
.
Регулярные выражения
(a+b)(a+b)(a+b)
и
ab(a+b)+(a+b)ab+b(a+b)(a+b)+(a+b)(a+b)a
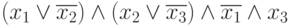

Упражнение 15.9.3. Равны ли регулярные выражения
(a+b)(a+b)(a+b)
и
bb(a+b)+ba(a+b)+a(a+b)b+(a+b)aa ?
Упражнение 15.9.4. Равны ли регулярные выражения
(a+b)(a+b)(a+b)(a+b)
и
aab(a+b)+a(a+b)(a+b)b+(a+b)aa(a+b)+(a+b)bb(a+b)+
+(a+b)baa+bab(a+b)+b(a+b)(a+b)b ?Упражнение 15.9.5. Эквивалентен ли конечный автомат
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" <0.6mm> ^{a}
\ar "1,2" <-0.6mm> _{b}
& *=[o][F-]{2}
\ar "1,3" <0.6mm> ^{a}
\ar "1,3" <-0.6mm> _{b}
& *=[o][F-]{3}
\ar "1,4" <0.6mm> ^{a}
\ar "1,4" <-0.6mm> _{b}
& *=[o][F=]{4}
}](/sites/default/files/tex_cache/5b108c69279a963ed6b7285ccced6d6f.png)
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{0}
\ar @`{+/l16mm/} [] ^{}
\ar "4,1" <0.6mm> ^{a}
\ar "4,1" <-0.6mm> _{b}
\ar "2,2" ^{a}
\ar "1,4" _{b}
&
&
& *=[o][F-]{4}
\ar "4,4" <0.6mm> ^{a}
\ar "4,4" <-0.6mm> _{b}
\ar "2,3" _{b}
\\
%
& *=[o][F-]{2}
\ar "3,2" <0.6mm> ^{a}
\ar "3,2" <-0.6mm> _{b}
\ar "2,3" ^{a}
& *=[o][F-]{6}
\ar "3,3" <0.6mm> ^{a}
\ar "3,3" <-0.6mm> _{b}
&
\\
%
& *=[o][F-]{3}
\ar "3,3" _{a}
& *=[o][F=]{7}
&
\\
*=[o][F-]{1}
\ar "3,2" _{a}
\ar "4,4" ^{b}
&
&
& *=[o][F-]{5}
\ar "3,3" ^{b}
}](/sites/default/files/tex_cache/df5e862d87e2d6b809174f5a060e0a6b.png)
