|
Упражнение 2.1.25 |
Слова, языки и грамматики
1.2. Операции над языками
Определение 1.2.1.
Пусть 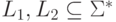 .
Тогда
.
Тогда

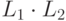 называется конкатенацией
языков L1 и L2.
называется конкатенацией
языков L1 и L2.Пример 1.2.2. Если L1 = {a,abb}
и L2 = {bbc,c},
то 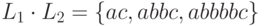 .
.
Упражнение 1.2.3.
При каких положительных целых числах k, l, m, n
существуют алфавит  ,
язык
,
язык 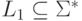 и язык
и язык 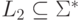 ,
удовлетворяющие условиям
,
удовлетворяющие условиям  , |L1| = l, |L2| = m,
, |L1| = l, |L2| = m, 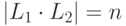
Определение 1.2.4. Пусть  .
Тогда
.
Тогда

Пример 1.2.5. Если L = {akbal | 0 < k < l}, то L2 = {akbalbam | 0 < k < l - 1, m > 1}.
Упражнение 1.2.6. Пусть 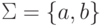 и L = {aa,ab}.
Найти L3.
и L = {aa,ab}.
Найти L3.
Определение 1.2.7. Итерацией языка (Kleene closure) языка L (обозначение L* ) называется язык

Пример 1.2.8.
Если 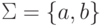 и L = {aa,ab,ba,bb},
то
и L = {aa,ab,ba,bb},
то
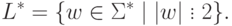
Упражнение 1.2.9. Пусть 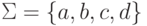 и
и

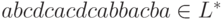
Упражнение 1.2.10. Существует ли такой язык L,
что выполняется неравенство 
Определение 1.2.11. Обращением или зеркальным образом слова w (обозначается wR ) называется слово, в котором символы, составляющие слово w, идут в обратном порядке.
Пример 1.2.12. Если w = baaca, то wR = acaab.
Определение 1.2.13. Пусть  .
Тогда
.
Тогда
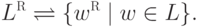
Упражнение 1.2.14.
Существует ли такой язык L,
что выполняется неравенство  ?
?
Определение 1.2.15. Говорят, что слово x - префикс ( начало ) слова y
(обозначение  ),
если y = xu
для некоторого слова u.
),
если y = xu
для некоторого слова u.
Пример 1.2.16. Очевидно,
что 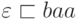 ,
, 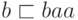 ,
,  и
и 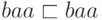 .
.
Определение 1.2.17. Пусть  .
Тогда через Pref(L)
обозначается множество, состоящее из всех префиксов
слов языка L:
.
Тогда через Pref(L)
обозначается множество, состоящее из всех префиксов
слов языка L:

Определение 1.2.18 Говорят,
что слово x - суффикс
( конец ) слова y
(обозначение  ),
если y = ux
для некоторого слова u.
),
если y = ux
для некоторого слова u.
Определение 1.2.19. Пусть  .
Тогда через Suf(L)
обозначается множество, состоящее из всех суффиксов
слов языка L:
.
Тогда через Suf(L)
обозначается множество, состоящее из всех суффиксов
слов языка L:

Определение 1.2.20. Говорят, что слово x - подслово (substring) слова y, если y = uxv для некоторых слов u и v.
Определение 1.2.21. Пусть  .
Тогда через Subw(L)
обозначается множество, состоящее из всех подслов
слов языка L.
Множество Subw(L)
называется множеством подслов
языка L.
.
Тогда через Subw(L)
обозначается множество, состоящее из всех подслов
слов языка L.
Множество Subw(L)
называется множеством подслов
языка L.
Определение 1.2.22. Слово a1a2...an
(длины 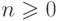 )
называется подпоследовательностью (subsequence)
слова y,
если существуют такие слова u0, u1, ..., un,
что u0a1u1a2...anun = y.
)
называется подпоследовательностью (subsequence)
слова y,
если существуют такие слова u0, u1, ..., un,
что u0a1u1a2...anun = y.
Замечание 1.2.23. Все подслова слова y являются также подпоследовательностями слова y.
Определение 1.2.24. Пусть  .
Тогда через Subseq(L)
обозначается множество, состоящее из всех подпоследовательностей
слов языка L.
Множество Subseq(L)
называется множеством подпоследовательностей
языка L.
.
Тогда через Subseq(L)
обозначается множество, состоящее из всех подпоследовательностей
слов языка L.
Множество Subseq(L)
называется множеством подпоследовательностей
языка L.
Пример 1.2.25.
Рассмотрим язык L = {cba, c}
над алфавитом {a, b, c}.
Очевидно, что 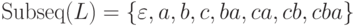 .
.
Определение 1.2.26. Функция 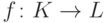 называется биекцией (bijection),
если каждый элемент множества L
является образом ровно одного элемента множества K
(относительно функции f ).
называется биекцией (bijection),
если каждый элемент множества L
является образом ровно одного элемента множества K
(относительно функции f ).
Определение 1.2.27. Множества K и L называются равномощными (of equal cardinality), если существует биекция из K в L.
Упражнение 1.2.28. Существуют ли такие языки L1 и L2,
что языки 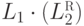 и
и 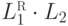 неравномощны?
неравномощны?
Упражнение 1.2.29. Существуют ли такие языки L1 и L2,
что языки 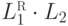 и
и 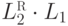 неравномощны?
неравномощны?
