|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Простые числа
Теорема Эйлера
Теорему Эйлера можно представить как обобщения малой теоремы Ферма. Модуль в теореме Ферма — простое число, модуль в теореме Эйлера — целое число. Мы вводим две версии этой теоремы.
Первая версия
Первая версия теоремы Эйлера подобна первой версии малой теоремы Ферма. Если a и n – взаимно простые, то 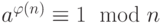 .
.
Вторая версия
Вторая версия теоремы Эйлера подобна второй версии малой теоремы Ферма; она устраняет условие, что n должно быть взаимно простым с a. Если 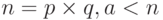 , а k — целое число, то
, а k — целое число, то  .
.
Приведем нестрогое доказательство второй версии, основанной на первой версии. Поскольку a < n, то возможны три случая:
1. Если a не кратно ни числу p, ни числу q, то a и n – взаимно простые.
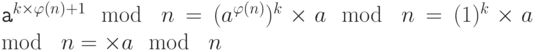
2. Если a — кратное число p, 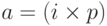 , но не кратно числу q.
, но не кратно числу q.
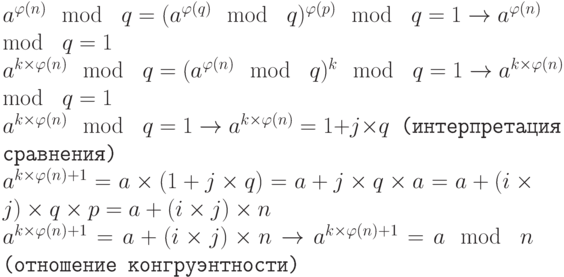
3. Если a кратно q (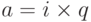 ), но не кратно p, доказательство второго случая то же самое, но p и q меняются местами.
), но не кратно p, доказательство второго случая то же самое, но p и q меняются местами.
Приложения
Хотя мы рассмотрим некоторые приложения теоремы Эйлера позже в этой лекции, теорема очень полезна для того, чтобы решать некоторые задачи.
Возведение в степень. Теорема Эйлера иногда полезна, чтобы быстро найти решение некоторых задач с возведением в степень. Следующие примеры показывают идею этого процесса.
Пример 12.15
Найдите результат 624 mod 35.
Решение
Мы имеем 
Пример 12.16
Найдите результат 2062 mod 77.
Решение
Если введем k = 1 согласно второй версии, мы имеем:
2062 mod 77 = (20 mod 77) mod 77 = (20)(20) mod 77 = 15
Мультипликативные инверсии. Теорема Эйлера может использоваться, чтобы найти мультипликативную инверсию по простому модулю. Теорема Эйлера может применяться, чтобы найти мультипликативные инверсии по составному модулю. Если n и a – взаимно простые, то  . Это может быть легко доказано умножением обеих сторон равенства на a.
. Это может быть легко доказано умножением обеих сторон равенства на a.
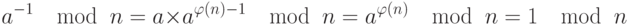
Пример 12.17
Мультипликативная инверсия по составному модулю может быть найдена без использования расширенного евклидова алгоритма, если мы знаем разложение на множители составного объекта:
a. 
b. 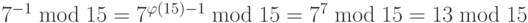
c. 
d. 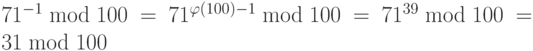
Генерация простых чисел
Два математика, Мерсенна и Ферма, попытались получить формулу, которая могла бы генерировать простые числа.
Простые числа Мерсенны
Мерсенна предложил следующую формулу, которую называют номера Мерсенны. Он предполагал, что формула перечисляет все простые числа.
Если p в приведенной выше формуле — простое число, то, как предполагали, Mp должно быть простым числом. Годы спустя было доказано, что не все числа, полученные по формуле Мерсенны, — простые числа. Ниже приведен список некоторых номеров Мерсенны.

Оказалось, что M11 — не простое число. Однако было найдено, что 41 число по формуле Мерсенны — простые; одно из последних найденных чисел Мерсенны — М124036583, наибольшее число содержит 7 253 733 цифр. Поиск продолжается.
Ферма пробовал найти формулу, которая генерирует простые числа. Следующая формула — для чисел Ферма:
Простые числа Ферма
Ферма попытался найти формулу для генерации простых чисел. Он предложил следующую формулу, которая теперь называется формулой Ферма, и проверил номера от F0 (n=0,1,…) до F4, но оказалось, что уже F4 — не простое число.
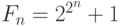
F0 = 3
F1 = 17
F2 = 257
F3 = 65537
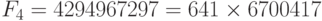 . Не простое число
. Не простое число
Фактически было доказано, что многие номера до F24 — составные числа.

