Сетевое планирование и управление
Анализ сетевой модели
Параметры сетевой модели. Параметрами сетевой модели являются:
- наиболее ранее возможное время наступления
 -го события,
обозначаемое символом
-го события,
обозначаемое символом 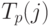 ;
; - самое позднее допустимое время наступления
 -го события,
обозначаемое символом
-го события,
обозначаемое символом 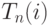 ;
; - резерв времени данного события, обозначаемый символом
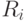 ;
; - полный резерв времени работы
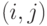 , обозначаемый символом
, обозначаемый символом 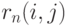 ;
; - свободный резерв времени работы
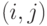 , обозначаемый символом
, обозначаемый символом  .
.
Наиболее раннее возможное время наступления  -го события
определяется следующей рекуррентной формулой:
-го события
определяется следующей рекуррентной формулой:
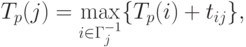 |
( 14.1) |
где 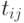 —
продолжительность
—
продолжительность 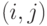 -й
работы;
-й
работы; 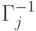 — множество событий, предшествующих
— множество событий, предшествующих  -му событию.
-му событию.
Вычисления по формуле (14.1) выполняются шаг за шагом, двигаясь в порядке нумерации событий.
Самое позднее допустимое время наступления события  определяется с помощью аналогичной рекуррентной формулы, но обращаясь не
к предшествующим, а к последующим событиям.
определяется с помощью аналогичной рекуррентной формулы, но обращаясь не
к предшествующим, а к последующим событиям.
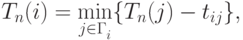 |
( 14.2) |
где 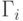 —
множество событий, следующих за
—
множество событий, следующих за  -м событием.
-м событием.
Для определения 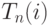 по формуле (14.2) надо двигаться от
конечного события
по формуле (14.2) надо двигаться от
конечного события  к исходному событию 0, при
этом
к исходному событию 0, при
этом  .
.
Резервом времени данного события называется
разность между 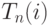 и
и 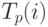 , которая вычисляется по формуле
, которая вычисляется по формуле
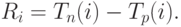 |
( 14.3) |
Полный резерв времени работы 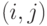 вычисляется по формуле
вычисляется по формуле
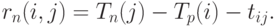 |
( 14.4) |
Свободный резерв времени работы 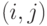 вычисляется по формуле
вычисляется по формуле
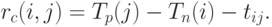 |
( 14.5) |
