|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Теоретические сведения о компьютерных вирусах
Формализм Ф. Лейтольда
В 2000-м году венгерский исследователь Ференц Лейтольд попытался дать новый импульс развитию математической теории компьютерных вирусов путем более точного моделирования вычислительной среды - компьютеров и операционных систем. Попутно он вывел некую общую классификацию вирусов и также, как Д. Чесс и С. Вайт, рассмотрел в рамках предложенного формализма феномен полиморфных вирусов.
Вычислительные модели
Вычислительная машина с произвольной выборкой
Для моделирования компьютерной среды Ф. Лейтольд отталкивался от вычислительной машины с произвольной выборкой (Random Access Machine, RAM), определение которой представлено ниже.
Вычислительная машина с произвольной выборкой состоит из следующих компонентов:
- Входная лента, представляющая собой последовательность ячеек, содержащих целые числа и доступных только для последовательного чтения - после чтения ячейки считывающая головка автоматически перемещается вправо
- Выходная лента, представляющая собой последовательность ячеек, доступных только для последовательной записи, по умолчанию эти ячейки пусты
- Программа - последовательность (возможно индексированная, т.е. с возможностью указать адрес некоторых или любых инструкций) инструкций, не находящаяся в памяти и, соответственно, неизменяемая, по умолчанию выполнение программы начинается с первой инструкции (можно ввести счетчик инструкций, указывающий на следующую к выполнению инструкцию, в этом случае по умолчанию счетчик указывает на первую инструкцию)
- Память - неограниченная последовательность регистров r0, r1, ..., ri, ..., способных хранить целые числа, по умолчанию значения регистров пусты, нулевой регистр r0 используется для вычислений и часто называется аккумулятором, доступ к регистрам производится непосредственно по их индексам, откуда и происходит название машины.
Как следует из определения, после того как ячейка была прочитана или записана, она не может быть прочитана или записана еще раз. Неизменяемость программы означает в том числе и то, что программа не может менять себя в процессе выполнения. Фактический набор используемых в программе инструкций большого значения не имеет, поскольку вычислительная сложность алгоритма реализованного в разных (разумных) наборах инструкций асимптотически будет совпадать. Один из возможных вариантов инструкций для вычислительной машины с произвольной выборкой представлен в таблице:
| Инструкция | Параметр | Описание |
|---|---|---|
| LOAD | Операнд | Загружает в память значение, определяемое операндом |
| STORE | Операнд | Копирует значение аккумулятора в ячейку памяти (регистр) определяемый операндом |
| ADD | Операнд | Добавляет к аккумулятору значение, определяемое операндом |
| SUB | Операнд | Вычитает из аккумулятора значение, определяемое операндом |
| MULT | Операнд | Умножает аккумулятор на значение, определяемое операндом |
| DIV | Операнд | Делит аккумулятор на значение, определяемое операндом |
| READ | Операнд | Считывает значение с входящей ленты в регистр, определяемый операндом |
| WRITE | Операнд | Записывает на выходную ленту значение, определяемое операндом |
| JUMP | Метка | Присваивает счетчику инструкций значение метки |
| JGTZ | Метка | Присваивает счетчику инструкций значение метки, если аккумулятор содержит положительное число |
| JZERO | Метка | Присваивает счетчику инструкций значение метки, если аккумулятор равен нулю |
| HALT | Завершает работу машины |
Допускается три вида операндов:
- i - обозначает собственно значение целого числа i
- [i] - для неотрицательных i обозначает значение регистра ri
- [[i]] - косвенная адресация, обозначает значение регистра rj, где j - значение регистра ri. Если j<0, машина завершает работу
По умолчанию (см. также определение) значение всех регистров равно нулю, счетчик инструкций указывает на первую инструкцию программы и выходная лента пуста. После выполнения k -й инструкции счетчик либо автоматически увеличивается на единицу и указывает на (k+1) -ю инструкцию, либо, если была выполнена инструкция JUMP или выполнены условия инструкций JGTZ или JZERO, принимает значение метки, либо, если была выполнена инструкция HALT, машина прекращает свою работу.
Вычислительная машина с хранением программ в памяти с произвольной выборкой
Развитием формализма вычислительной машины с произвольной выборкой является вычислительная машина с хранением программ в памяти с произвольной выборкой (Random Access Stored Program Machine, RASPM), отличие которой состоит только в том, что программа сохраняется в памяти, а значит может изменять сама себя в процессе выполнения.
Набор инструкций для RASPM в общем случае может не отличаться от набора инструкций RAM. Впрочем, некоторые инструкции могут быть упрощены. Так, вместо непрямой адресации можно использовать возможность модификации инструкций программы для получения того же эффекта.
Известно, что имеют место две теоремы:
Теорема 2.1. Если стоимость инструкции является величиной постоянной или находится в логарифмической зависимости от длины операнда, то для любой программы RAM, имеющей сложность T(n), найдется константа k и эквивалентная программа RASPM, сложность которой будет не больше kT(n).
Теорема 2.2. Если стоимость инструкции является величиной постоянной или находится в логарифмической зависимости от длины операнда, то для любой программы RASPM, имеющей сложность T(n), найдется константа k и эквивалентная программа RAM, сложность которой будет не больше kT(n).
Машина Тьюринга
Большинство теоретических результатов относительно вычислительной способности различных автоматов (к которым относятся RAM и RASPM) получено для Машины Тьюринга. Следовательно, для применения к RASPM уже известных результатов, необходимо установить отношение между этими формальными системами.
Определение 2.5. Машина Тьюринга с одной лентой может быть определена как совокупность семи элементов:
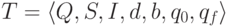 ,
,
где Q - множество состояний Машины Тьюринга, S - множество символов,
которые могут быть записаны на ленте, I - множество символов входящей
последовательности, 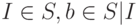 -
пустой символ, q0 - начальное состояние Машины Тьюринга, qf -
конечное состояние Машины Тьюринга, d: Q x S -> Q x S x {l, r, s}
- множество функций перехода, которые состоянию
и символу ленты ставят в соответствие новое состояние, новый символ и перемещение по
ленте: на шаг влево, на шаг вправо, остаться на месте
-
пустой символ, q0 - начальное состояние Машины Тьюринга, qf -
конечное состояние Машины Тьюринга, d: Q x S -> Q x S x {l, r, s}
- множество функций перехода, которые состоянию
и символу ленты ставят в соответствие новое состояние, новый символ и перемещение по
ленте: на шаг влево, на шаг вправо, остаться на месте
Машина начинает свою работу в состоянии q0 и в дальнейшем меняет состояния согласно функциям перехода в зависимости от текущего состояния и значения ячейки ленты. Попутно ячейки ленты перезаписываются новыми значениями согласно тем же функциям перехода.
Машина Тьюринга может содержать и большее количество лент, но вычислительная способность такой машины будет находиться в полиномиальной зависимости от вычислительной способности Машины Тьюринга с одной лентой. Помимо этого имеют место следующая теорема:
Кроме того доказан фундаментальный результат.

