|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Описание неопределенностей в теории принятия решений
Теория нечеткости является обобщением интервальной математики. Действительно, функция принадлежности
![\mu_B(x)=\begin{cases}
1, x \in [a,b]\\
0, x \notin [a,b]
\end{cases}](/sites/default/files/tex_cache/2030aeca46dad95e349b63d33b6dc7fd.png)
задает интервальную неопределенность - про рассматриваемую величину известно лишь, что она лежит в заданном интервале ![[a,b]](/sites/default/files/tex_cache/edf97e7650f93d7606ba4990a3a8f251.png) . Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.
. Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.
Начало современной теории нечеткости положено работой 1965 г. американского ученого азербайджанского происхождения Л.А. Заде. К настоящему времени по этой теории опубликованы тысячи книг и статей, издается несколько международных журналов, выполнено достаточно много как теоретических, так и прикладных работ. Первая книга российского автора по теории нечеткости вышла в 1980 г.
Сам Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от "принадлежности" к "непринадлежности" не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятием, качеством продукции и технологическими процессами.
Л.А. Заде использовал термин "fuzzy set" (нечеткое множество). На русский язык термин "fuzzy" переводили как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный.
Аппарат теории нечеткости громоздок. В качестве примера дадим определения теоретико-множественных операций над нечеткими множествами. Пусть  и
и  - два нечетких подмножества
- два нечетких подмножества  с функциями принадлежности
с функциями принадлежности  и
и 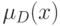 соответственно. Пересечением
соответственно. Пересечением 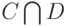 , произведением
, произведением 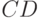 , объединением
, объединением 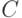 , отрицанием
, отрицанием 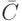 , суммой
, суммой 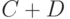 называются нечеткие подмножества
называются нечеткие подмножества  с функциями принадлежности
с функциями принадлежности
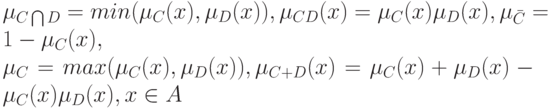
соответственно.
Как уже отмечалось, теория нечетких множеств в определенном смысле сводится к теории вероятностей, а именно, к теории случайных множеств. Однако при решении прикладных задач вероятностно-статистические методы и методы теории нечеткости обычно рассматриваются как различные.
Для знакомства со спецификой нечетких множеств рассмотрим некоторые их свойства.
В дальнейшем считаем, что все рассматриваемые нечеткие множества являются подмножествами одного и того же множества  .
.
Законы де Моргана для нечетких множеств. Как известно, законами де Моргана называются следующие тождества алгебры множеств
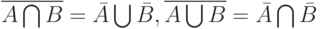 |
( 5) |
Теорема 1. Для нечетких множеств справедливы тождества
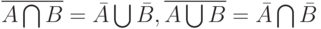 |
( 6) |
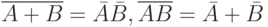 |
( 7) |
Доказательство теоремы 1 состоит в непосредственной проверке справедливости соотношений (6) и (7) путем вычисления значений функций принадлежности участвующих в этих соотношениях нечетких множеств на основе определений, данных выше.
Тождества (6) и (7) назовем законами де Моргана для нечетких множеств. В отличие от классического случая соотношений (5), они состоят из четырех тождеств, одна пара которых относится к операциям объединения и пересечения, а вторая - к операциям произведения и суммы. Как и соотношения (5) в алгебре множеств, законы де Моргана в алгебре нечетких множеств позволяют преобразовывать выражения и формулы, в состав которых входят операции отрицания.
Дистрибутивный закон для нечетких множеств. Некоторые свойства операций над множествами не выполнены для нечетких множеств. Так, 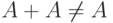 за исключением случая, когда
за исключением случая, когда  - "четкое" множество (т.е. функция принадлежности принимает только значения 0 и 1).
- "четкое" множество (т.е. функция принадлежности принимает только значения 0 и 1).
Верен ли дистрибутивный закон для нечетких множеств? В литературе иногда расплывчато утверждается, что "не всегда". Внесем полную ясность.
Теорема 2. Для любых нечетких множеств  ,
, 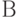 и
и 
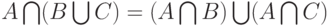 |
( 8) |
В то же время равенство
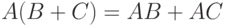 |
( 9) |
справедливо тогда и только тогда, когда при всех 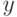
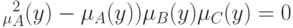
Доказательство. Фиксируем произвольный элемент 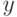 . Для сокращения записи обозначим
. Для сокращения записи обозначим 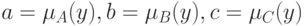 Для доказательства тождества (8) необходимо показать, что
Для доказательства тождества (8) необходимо показать, что
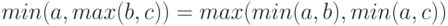 |
( 10) |
Рассмотрим различные упорядочения трех чисел 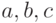 . Пусть сначала
. Пусть сначала 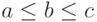 Тогда левая часть соотношения (10) есть
Тогда левая часть соотношения (10) есть 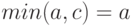 а правая
а правая 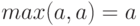 т.е. равенство (10) справедливо.
т.е. равенство (10) справедливо.
Пусть 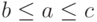 Тогда в соотношении (10) слева стоит
Тогда в соотношении (10) слева стоит 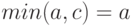 а справа
а справа 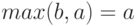 т.е. соотношение (10) опять является равенством.
т.е. соотношение (10) опять является равенством.
Если 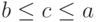 то в соотношении (10) слева стоит
то в соотношении (10) слева стоит 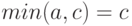 а справа
а справа 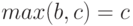 т.е. обе части снова совпадают.
т.е. обе части снова совпадают.
Три остальные упорядочения чисел a, b, c разбирать нет необходимости, поскольку в соотношение (10) числа b и c входят симметрично. Тождество (8) доказано.
Второе утверждение теоремы 2 вытекает из того, что в соответствии с определениями операций над нечеткими множествами
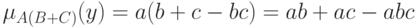
и
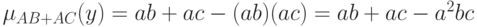
Эти два выражения совпадают тогда и только тогда, когда  что и требовалось доказать.
что и требовалось доказать.
Определение 1. Носителем нечеткого множества  называется совокупность всех точек
называется совокупность всех точек 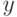 , для которых
, для которых 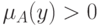
Следствие теоремы 2. Если носители нечетких множеств В и С совпадают с У, то равенство (9) имеет место тогда и только тогда, когда А - "четкое" (т.е. обычное, классическое, не нечеткое) множество.
Доказательство. По условию 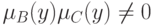 при всех
при всех 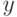 . Тогда из теоремы 2 следует, что
. Тогда из теоремы 2 следует, что  т.е.
т.е. 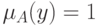 или
или 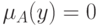 , что и означает, что
, что и означает, что  - четкое множество.
- четкое множество.
Пример описания неопределенности с помощью нечеткого множества. Понятие "богатый" часто используется при обсуждении социально-экономических проблем, в том числе и в связи с подготовкой и принятием решений. Однако очевидно, что разные лица вкладывают в это понятие различное содержание. Сотрудники Института высоких статистических технологий и эконометрики провели в 1996 г. социологическое исследование представления различных слоёв населения о понятии "богатый человек".
Мини-анкета опроса выглядела так:
- При каком месячном доходе (в млн. руб. на одного человека) Вы считали бы себя богатым человеком?
- Оценив свой сегодняшний доход, к какой из категорий Вы себя относите:
- богатые;
- достаток выше среднего;
- достаток ниже среднего;
- бедные;
- за чертой бедности?
- (В дальнейшем вместо полного наименования категорий будем оперировать буквами, например "в" - категория, "б" - категория и т.д.)
- Ваша профессия, специальность.
Всего было опрошено 74 человека, из них 40 - научные работники и преподаватели, 34 человека - не занятых в сфере науки и образования, в том числе 5 рабочих и 5 пенсионеров. Из всех опрошенных только один (!) считает себя богатым. Несколько типичных ответов научных работников и преподавателей приведено в табл. 9.1, а аналогичные сведения для работников коммерческой сферы - в табл.9.2.
| Ответы на вопрос 3 | Ответы на вопрос 1, млн. руб./чел. | Ответы на вопрос 2 | Пол |
|---|---|---|---|
| Кандидат наук | 1 | д | ж |
| Преподаватель | 1 | в | ж |
| Доцент | 1 | б | ж |
| Учитель | 10 | в | м |
| Старший. научный сотрудник | 10 | д | м |
| Инженер-физик | 24 | д | ж |
| Программист | 25 | г | м |
| Научный работник | 45 | г | м |
| Ответы на вопрос 3 | Ответы на вопрос 1 | Ответы на вопрос 2 | Пол |
|---|---|---|---|
| Вице-президент банка | 100 | а | ж |
| Зам. директора банка | 50 | б | ж |
| Начальник. кредитного отдела | 50 | б | м |
| Начальник отдела ценных бумаг | 10 | б | м |
| Главный бухгалтер | 20 | д | ж |
| Бухгалтер | 15 | в | ж |
| Менеджер банка | 11 | б | м |
| Начальник отдела проектирования | 10 | в | ж |
Разброс ответов на первый вопрос - от 1 до 100 млн. руб. в месяц на человека. Результаты опроса показывают, что критерий богатства у финансовых работников в целом несколько выше, чем у научных (см. гистограммы на. рис 9.1 и рис.9.29.2 ниже).
Опрос показал, что выявить какое-нибудь конкретное значение суммы, которая необходима "для полного счастья", пусть даже с небольшим разбросом, нельзя, что вполне естественно. Как видно из таблиц 9.1 и 9.2, денежный эквивалент богатства колеблется от 1 до 100 миллионов рублей в месяц. Подтвердилось мнение, что работники сферы образования в подавляющем большинстве причисляют свой достаток к категории "в" и ниже (81% опрошенных), в том числе к категории "д" отнесли свой достаток 57%.
Со служащими коммерческих структур и бюджетных организаций иная картина: "г" - категория 1 человек (4%), "д" - категория 4 человека (17%), "б" - категория - 46% и 1 человек "а" - категория.
Пенсионеры, что не вызывает удивления, отнесли свой доход к категории "д" (4 человека), и лишь один человек указал "г" - категорию. Рабочие же ответили так: 4 человека - "в", и один человек - "б".
Для представления общей картины в табл. 9.3 приведены данные об ответах работников других профессий.
| Ответы на вопрос 3 | Ответы на вопрос 1 | Ответы на вопрос 2 | Пол |
|---|---|---|---|
| Работник торговли | 1 | б | ж |
| Дворник | 2 | в | ж |
| Водитель | 10 | в | м |
| Военнослужащий | 10 | в | м |
| Владелец бензоколонки | 20 | б | ж |
| Пенсионер | 6 | д | ж |
| Начальник фабрики | 20 | б | м |
| Хирург | 5 | в | м |
| Домохозяйка | 10 | в | ж |
| Слесарь-механик | 25 | в | м |
| Юрист | 10 | б | м |
| Оператор ЭВМ | 20 | д | м |
| Работник собеса | 3 | д | ж |
| Архитектор | 25 | б | ж |

