|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Принятие решений при управлении инновационными и инвестиционными проектами
Многие специалисты при расчете срока окупаемости инвестиций рекомендуют учитывать временной аспект. В этом случае в расчет принимаются дисконтированные денежные потоки, например, по показателю 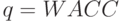 , а соответствующая формула для расчета дисконтированного срока окупаемости, DPP (Discounted Payback Period) , имеет вид:
, а соответствующая формула для расчета дисконтированного срока окупаемости, DPP (Discounted Payback Period) , имеет вид:

при котором
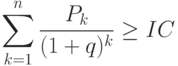
Очевидно, что в случае дисконтирования срок окупаемости увеличивается, т.е. всегда  . Иными словами, проект, приемлемый по критерию РР, может оказаться неприемлемым по критерию DPP. Очевидно, что показатель РР соответствует случаю, когда
. Иными словами, проект, приемлемый по критерию РР, может оказаться неприемлемым по критерию DPP. Очевидно, что показатель РР соответствует случаю, когда 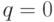 .
.
Итак, срок окупаемости - тот срок, за который доходы покроют расходы. Предполагается, что после этого проект (инвестиционный проект, или проект изменения налоговой системы, в частности, ставок налогов, или же какой-либо иной) приносит только прибыль. Очевидно, это верно не для всех проектов. Например, если проект состоит из нескольких стадий, то расходы, связанные с началом второй стадии, могут превысить доходы, достигнутые в результате осуществления первой стадии. Потому понятие "срок окупаемости" применяют прежде всего к тем проектам, в которых за единовременным вложением средств следует ежегодное получение прибыли.
Пример 2. Рассмотрим финансовый поток с одним платежом (инвестициями) a(0) = (-А) и дальнейшими поступлениями  .
.
Простейший (и, как пояснено выше, наименее обоснованный) способ расчета срока окупаемости состоит в делении объема вложений А на ожидаемый ежегодный доход В. Тогда срок окупаемости РР равен А/В.
Пусть, например, А - это разовое уменьшение налоговых сборов в результате снижения ставок, а В - ожидаемый ежегодный прирост поступлений в бюджет, обеспеченный расширением налоговой базы в результате ускоренного развития производства.
Этот способ расчета срока окупаемости не учитывает дисконтирование. К чему приведет введение в расчет дисконтирования? Пусть, как и ранее, объем единовременных вложений равен А, причем, начиная с конца первого года, проект дает доход В ежегодно (точнее, доход поступает порциями, равными В, с момента, наступающего через год после вложения капитала, и далее с интервалом в год). Если дисконт-фактор равен С, то максимально возможный суммарный доход равен

В скобках стоит сумма бесконечной геометрической прогрессии, равная, как известно, величине 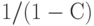 . Следовательно, максимально возможный суммарный доход от первого года после вложения капитала до скончания мира равен
. Следовательно, максимально возможный суммарный доход от первого года после вложения капитала до скончания мира равен 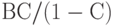 .
.
Отсюда следует, что если  меньше
меньше 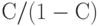 , то можно указать (рассчитать) срок окупаемости проекта, но он будет больше, иногда существенно больше, чем
, то можно указать (рассчитать) срок окупаемости проекта, но он будет больше, иногда существенно больше, чем  . Если же
. Если же  больше или равно
больше или равно 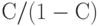 , то проект не окупится никогда. Поскольку максимально возможное значение С равно 0,89, то проект не окупится никогда, если
, то проект не окупится никогда. Поскольку максимально возможное значение С равно 0,89, то проект не окупится никогда, если  не меньше
не меньше 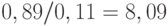 .
.
Пример 3. Пусть вложения равны 1 миллиону рублей, ежегодная прибыль составляет 500 тысяч, т.е. 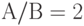 . Пусть дисконт-фактор
. Пусть дисконт-фактор 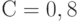 . Каков срок окупаемости? При примитивном подходе (соответствующем
. Каков срок окупаемости? При примитивном подходе (соответствующем 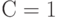 ) он равен
) он равен  годам. А на самом деле?
годам. А на самом деле?
За k лет будет возвращено
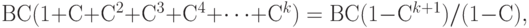
согласно известной формуле для суммы конечной геометрической прогрессии. Для срока окупаемости получаем уравнение
 |
( 6) |
откуда  , или
, или  . Прологарифмируем обе части последнего уравнения: (k+1) ln 0,8 = ln 0,5 , откуда
. Прологарифмируем обе части последнего уравнения: (k+1) ln 0,8 = ln 0,5 , откуда

Срок окупаемости оказался в данном примере равном 2,11 лет, т.е. увеличился примерно на 6 недель. Это немного. Однако если 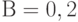 , то вместо (6) мы имеем
, то вместо (6) мы имеем

Это уравнение не имеет решения, поскольку  , проект не окупится никогда. Окупаемости можно ожидать лишь в случае
, проект не окупится никогда. Окупаемости можно ожидать лишь в случае 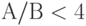 . Рассмотрим и промежуточный случай,
. Рассмотрим и промежуточный случай, 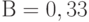 , с "примитивным" сроком окупаемости
, с "примитивным" сроком окупаемости 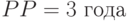 . Тогда вместо (6) имеем уравнение
. Тогда вместо (6) имеем уравнение
 |
( 7) |
откуда  , или
, или  . Прологарифмируем обе части последнего уравнения:
. Прологарифмируем обе части последнего уравнения: 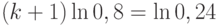 , откуда
, откуда

Итак, реальный срок окупаемости - не три года, а согласно уравнению (7) чуть менее пяти с половиной лет.
Если вложения делаются не единовременно или доходы поступают по иной схеме, то расчеты усложняются, но суть дела остается той же.
Таким образом, срок окупаемости зависит от неизвестного дисконт-фактора С или даже от неизвестной дисконт-функции - ибо какие у нас основания считать будущую дисконт-функцию постоянной? Иногда (в том числе в официальных изданиях [4.11]) рекомендуется использовать норму дисконта (дисконт-фактор), соответствующую ПРИЕМЛЕМОЙ для инвестора норме дохода на капитал. Мы не знаем заранее, какую норму дисконта тот или иной инвестор сочтет приемлемой. Однако ясно, что она зависит от ситуации в экономике в целом. То, что представляется выгодным сегодня, может оказаться невыгодным завтра, или наоборот. Тем самым решение перекладывается на инвестора, который фактически выступает в роли эксперта по выбору нормы дисконта.
Коэффициент эффективности инвестиций. Этот критерий имеет две характерные черты: во-первых, он не предполагает дисконтирования показателей дохода; во-вторых, доход характеризуется показателем чистой прибыли PN (прибыль за минусом отчислений в бюджет). Алгоритм расчета исключительно прост, что и предопределяет широкое использование этого показателя на практике. Коэффициент эффективности инвестиции, называемый также учетной нормой прибыли (ARR - Accounting Rate of Return), рассчитывается делением среднегодовой прибыли PN на среднюю величину инвестиций (коэффициент берется в процентах). Средняя величина инвестиций находится делением исходной суммы капитальных вложений на два, если предполагается, что по истечении срока реализации анализируемого проекта все капитальные затраты будут списаны. Если допускается наличие остаточной или ликвидационной стоимости ( RV ), то ее оценка должна быть учтена в расчетах. Иными словами, существуют различные алгоритмы исчисления показателя ARR. Достаточно распространенным является следующий:

Данный показатель чаще всего сравнивается с коэффициентом рентабельности авансированного капитала, рассчитываемого делением общей чистой прибыли организации на общую сумму средств, авансированных в ее деятельность (итог среднего баланса-нетто).
Метод, основанный на коэффициенте эффективности инвестиции, также имеет ряд существенных недостатков, обусловленных в основном тем, что он не учитывает временной компоненты денежных потоков. В частности, метод не делает различия между проектами с одинаковой суммой среднегодовой прибыли, но варьирующей суммой прибыли по годам, а также между проектами, имеющими одинаковую среднегодовую прибыль, но генерируемую в течение различного количества лет, и т.п.
Критерии (показатели, характеристики) финансовых потоков используются для оценки и сравнения инвестиционных проектов, выбора из них наиболее предпочтительных для инвестора.

