|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Совершенно секретные системы
Расстояние единственности
Если криптографическая система не является совершенно секретной, то зашифрованное сообщение может дать криптоаналитику некоторую информацию об исходном сообщении. Специалист, может быть, и не сможет сразу однозначно дешифровать шифротекст, однако он будет иметь возможность делать некоторые предположения о ключе или открытом тексте. После получения каждого следующего зашифрованного тем же ключом сообщения криптоаналитик будет расширять свои знания относительно ключа шифрования и в конце концов сможет дешифровать сообщения.
Возникает вопрос, а какой должна быть длина зашифрованного сообщения, чтобы можно было однозначно дешифровать его. В примере, рассмотренном в лекции 2 проводилась попытка дешифрования сообщения из 11 символов, закрытого методом простой замены. На основе анализа статистических закономерностей русского языка удалось подобрать несколько подходящих вариантов открытых текстов, однако для выбора из них одного "правильного" не хватило информации. По-видимому, существует некоторая длина перехваченного сообщения, после которой сообщение может быть дешифровано с вероятностью, близкой к единице.
Шеннон ввел понятие расстояния единственности шифра (или расстояния уникальности ) U, которое показывает, сколько букв зашифрованного сообщения необходимо перехватить для однозначного восстановления ключа.
Для вычисления расстояния единственности необходимо знать энтропию ключа Н(К). Для симметричных шифров энтропия ключа примерно равна логарифму числа ключей NK по основанию 2:
Н(К) = log2 NK
Например, для шифра простой замены, применяемого к русскому языку, число возможных ключей определяется количеством всех возможных таблиц замен и равно 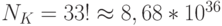 поэтому энтропия ключа будет равна
поэтому энтропия ключа будет равна
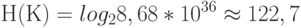
Если нам известна энтропия ключа Н(К) для некоторого шифра, то расстояние единственности U для него вычисляется по формуле
U = H(K) / D,
где D – избыточность шифруемого сообщения.
Рассчитаем расстояние единственности для шифра простой замены, применяемого к сообщению на русском языке:
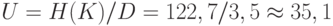
То есть если длина перехваченного зашифрованного сообщения превышает 35 символов, то его, скорее всего, можно будет однозначно дешифровать. А при длине зашифрованного текста меньше 35 символов возможно неоднозначное вскрытие.
Расстояние единственности показывает нам не то, какой размер должен иметь перехваченный шифротекст, чтобы его было легко дешифровать, а то, насколько большим он должен быть, чтобы было возможно в принципе его однозначное дешифрование.
Для того чтобы затруднить противнику определение ключа и дешифрование наших секретных сообщений, необходимо увеличивать (а желательно доводить до бесконечности) расстояние единственности в применяемых шифрах. Проанализировав формулу для вычисления расстояния единственности, определим, что это можно сделать двумя способами.
Если энтропия ключа равна бесконечности, то расстояние единственности шифра будет тоже равно бесконечности. Энтропия ключа тем больше, чем длиннее ключ. В случае использования системы одноразовой ленты ключ теоретически бесконечен и все его символы равновероятны, поэтому энтропия ключа такого шифра будет бесконечно большой. Следовательно, расстояние единственности шифра Вернама равно бесконечности.
Как уже отмечалось выше, использовать шифр с бесконечно большим ключом практически нецелесообразно. Однако на практике можно менять иногда ключ шифрования, тем самым затрудняя жизнь противнику. Специалисты рекомендуют использовать системы, в которых ключ меняется задолго до достижения расстояния единственности шифра. Этого можно достичь, например, используя сеансовые ключи шифрования, то есть применять для шифрования каждого сообщения новый ключ.
Второй способ увеличения расстояния единственности состоит в уменьшении избыточности исходного текста. Если избыточность сообщения равна нулю, то ключ никогда не будет определен, а зашифрованное сообщение вскрыто, так как расстояние единственности будет равно бесконечности. К сожалению, на практике такая ситуация невозможна, так как любое осмысленное сообщение будет иметь некоторую отличную от нуля избыточность.
Однако возможно уменьшение избыточности в сообщениях за счет сжатия данных. Дело в том, что при сжатии данных энтропия "сжатого" текста сохраняется, а длина уменьшается. Следовательно, энтропия на букву в сжатом тексте больше, чем в исходном, а избыточность – меньше. Значит, после сжимающего кодирования расстояние единственности шифра увеличивается.
Ключевые термины
Абсолютная норма языка – максимальное количество бит информации, которое может быть передано одним символом некоторого языка, при условии, что все последовательности символов в языке равновероятны.
Избыточность языка – статистическая величина, обозначающая избыточность информации, содержащейся в тексте на определённом языке.
Норма языка – величина, характеризующая количество информации, приходящееся на один символ сообщения.
Одноразовая лента (или одноразовый блокнот, или шифр Вернама) – один из возможных вариантов реализации совершенно секретной системы. Может быть реализован как гаммирование с бесконечной гаммой.
Расстояние единственности шифра (или расстояния уникальности) – величина, показывающая, сколько букв зашифрованного сообщения необходимо перехватить для однозначного восстановления ключа.
Совершенно секретная система – криптографическая система, для которой анализ зашифрованного текста не дает никакой информации об открытом тексте, кроме, возможно, его длины.
Энтропия сообщения – характеристика, введенная Шенноном. Определяет количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения. Является мерой неопределённости или непредсказуемости информации.
Краткие итоги
Основные положения теории информации, используемые в криптографии, были сформулированы в середине ХХ века. Большой вклад в эти исследования внес американский ученый К. Шеннон. Для исследования принципов передачи информации по коммуникационным каналам Шеннон предложил вероятностный подход к оценке количества передаваемой информации. Кроме того, он показал, что в принципе возможны так называемые совершенно секретные криптографические системы, которые не могут быть "взломаны".
Криптографическая система называется совершенно секретной, если анализ зашифрованного текста не может дать никакой информации об открытом тексте, кроме, возможно, его длины. Одним из возможных вариантов реализации совершенно секретной системы является шифр Вернама (или одноразовый блокнот, или одноразовая лента). Шифрование по этому методу выполняется как сложение по модулю два открытого текста с бесконечным ключом (называемым одноразовым блокнотом или шифроблокнотом). При этом ключ должен обладать тремя важными свойствами: быть истинно случайным; совпадать по размеру с заданным открытым текстом; применяться только один раз. Данный метод, к сожалению, не слишком удобен на практике. Во-первых, как и любые системы шифрования с закрытым ключом в них существует проблема распределения ключей. Во-вторых, в совершенной секретной системе ключ шифрования должен иметь по крайней мере такую же длину, как и открытый текст. Кроме того, для шифрования каждого сообщения должен применяться свой новый ключ. Все эти факторы делают реализацию совершенно секретной системы очень дорогой и не слишком удобной. Такие системы имеет смысл использовать лишь для самых важных линий связи, например, правительственных.
Если криптографическая система не является совершенно секретной, то знание шифротекста сообщения предоставляет некоторую информацию относительно соответствующего открытого текста. Большинство используемых на практике криптографических систем не является совершенно секретными.
Для увеличения безопасности реальных криптографических систем специалисты рекомендуют:
- использовать сеансовые ключи шифрования, то есть применять для шифрования каждого сообщения новый ключ;
- уменьшать избыточность шифруемых массивов данных, например, выполнять сжатие сообщений перед криптографическим шифрованием.
Набор для практики
Вопросы для самопроверки
- Как определяется энтропия источника сообщений?
- Что характеризует энтропия источника сообщений?
- Что определяет норма языка?
- Как вычисляется абсолютная норма языка?
- Что характеризует избыточность языка?
- Почему в сообщениях, составленных на естественных языках, всегда имеется избыточность?
- Дайте определение совершенно секретной криптографической системы.
- Приведите примеры шифров, которые не являются совершенно секретными системами.
- Почему шифр одноразовой ленты (шифр Вернама) является совершенно секретной системой?
- Почему совершенно секретные системы не используются повсеместно на практике для защиты информации?
- Как определяется энтропия ключа шифра?
- Каким образом вычисляется расстояние единственности для шифра?
Упражнения для самопроверки
- Источник генерирует 32 различных символа. Чему равно количество информации по Хартли, приходящееся на 1 символ?
- Некоторое устройство передачи данных может генерировать 256 различных символа. Чему равно количество информации по Хартли, приходящееся на сообщение из 10 символов?
- Известно, что для некоторого источника сообщений количество информации по Хартли, приходящееся на 1 символ, равно 6 битам. Чему равно количество символов в алфавите источника сообщений?
- Два источника генерируют по два символа. Первый источник генерирует символы с равными вероятностями, второй – с различными. Для какого источника количество информации по Шеннону, приходящееся на один символ, будет больше?
- Пусть источник сообщений может генерировать n разных сообщений m1, m2, ..., mn с вероятностями p1, p2,... , pn. Определите энтропию источника для заданных исходных данных:
- n = 4; p1 = 0,25, p2= 0,25, p3 = 0,375, p4 = 0,125
- n = 6; p1 = 0,0025, p2= 0,0075, p3 = 0,09, p4 = 0,2, p5= 0,5, p6 = 0,2
- n = 4; p1= 0,25, p2= 0,1, p3 = 0,15, p4 = 0,5
- Зашифруйте сообщение m шифром Вернама с ключом k:
- m = 1001001110, k = 0100111011
- m = 0101101110, k = 1010101011
- m = 1111001101, k = 0110001011
- 7. Рассчитайте энтропию ключа для шифра Цезаря со сдвигом на n позиций, применяемого для сообщений на русском языке ( 32 буквы ).
- 8. Рассчитайте расстояние единственности для шифра Цезаря со сдвигом на n позиций, применяемого для сообщений на русском языке ( 32 буквы ). Избыточность сообщений на русском языке принять равной 3,5 бит на символ.
- 9. Предполагая, что все варианты ключей равновероятны и возможны, рассчитайте расстояние единственности для шифров с заданной длиной двоичного ключа N, применяемых к сообщениям, избыточность которых составляет D:
- N=256 бит, D =3,5 ;
- N=512 бит, D =3 ;
- N=128 бит, D =4.

