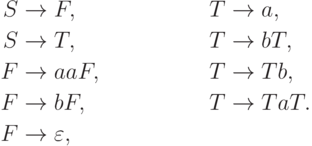| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Алгоритмически неразрешимые проблемы
16.2. Проблема однозначности
Теорема 16.2.1. Пусть  . Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом 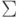 узнать, является ли грамматика G однозначной.
узнать, является ли грамматика G однозначной.
Доказательство.
Рассмотрим язык 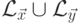 .
Следуя доказательству теоремы 9.4.3,
построим грамматику G
для этого языка, исходя из грамматик
.
Следуя доказательству теоремы 9.4.3,
построим грамматику G
для этого языка, исходя из грамматик 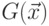 и
и 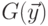 .
.
Грамматика G является неоднозначной тогда и только тогда, когда
постовская система соответствия 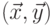 имеет решение.
имеет решение.
Упражнение 16.2.2. Однозначна ли контекстно-свободная грамматика
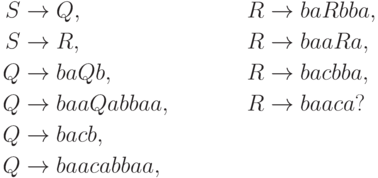
16.3. Дополнение контекстно-свободного языка
Лемма 16.3.1. Рассмотрим алфавит 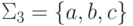 . Язык
. Язык  является контекстно-свободным при любом
является контекстно-свободным при любом 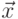 .
.
Пример 16.3.2.
Пусть 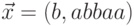 .
Тогда язык
.
Тогда язык  над алфавитом
над алфавитом 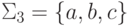 порождается контекстно-свободной грамматикой
порождается контекстно-свободной грамматикой
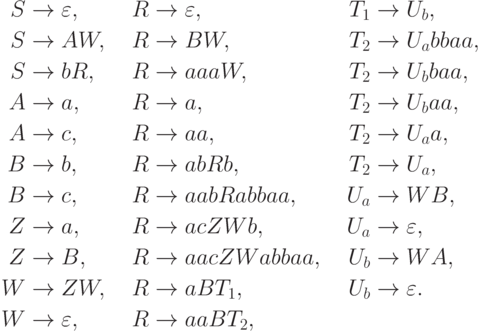
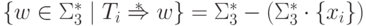 для каждого i.
для каждого i.Язык  является даже линейным
(чтобы получить линейную грамматику, достаточно "раскрыть"
вспомогательные символы A, B и Z ).
является даже линейным
(чтобы получить линейную грамматику, достаточно "раскрыть"
вспомогательные символы A, B и Z ).
Замечание 16.3.3.
Лемму 16.3.1
можно доказать, явно построив
контекстно-свободную грамматику
(как в примере 16.3.2),
а можно и вывести из теоремы 12.2.7},
проверив, что 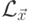 -
детерминированный контекстно-свободный язык.
-
детерминированный контекстно-свободный язык.
Определение 16.3.4.
Пусть 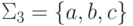 ,
, 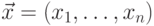 ,
,  ,
где
,
где  и
и 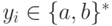 для всех i.
Обозначим через
для всех i.
Обозначим через 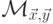 язык
язык 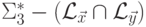 .
.
Лемма 16.3.5.
Язык 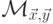 является контекстно-свободным
при любых
является контекстно-свободным
при любых 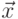 и
и 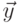 .
.
Доказательство. 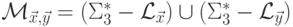 .
.
Лемма 16.3.6. Дополнение языка 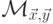 является непустым тогда и только тогда, когда
постовская система соответствия
является непустым тогда и только тогда, когда
постовская система соответствия 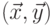 имеет решение.
имеет решение.
Доказательство Утверждение следует из леммы 16.1.2.
Теорема 16.3.7. Пусть  . Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом 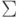 узнать, верно ли, что
узнать, верно ли, что 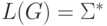 .
.
Доказательство
Очевидно, что 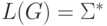 тогда и только тогда, когда
дополнение языка L(G)
является пустым.
тогда и только тогда, когда
дополнение языка L(G)
является пустым.
Теорема 16.3.8. Пусть  . Тогда не существует алгоритма, позволяющего по произвольным
контекстно-свободным грамматикам G1 и G2 над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольным
контекстно-свободным грамматикам G1 и G2 над алфавитом 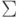 узнать, верно ли, что L(G1) = L(G2).
узнать, верно ли, что L(G1) = L(G2).
Доказательство Утверждение следует из предыдущей теоремы и примера 1.5.16.
Теорема 16.3.9. Пусть  . Тогда не существует алгоритма, позволяющего по произвольным
контекстно-свободным грамматикам G1 и G2 над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольным
контекстно-свободным грамматикам G1 и G2 над алфавитом 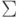 узнать, верно ли, что
узнать, верно ли, что  .
.
Доказательство
Очевидно, что 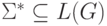 тогда и только тогда, когда
тогда и только тогда, когда 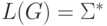 .
.
Лемма 16.3.10. Дополнение языка 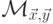 является бесконечным тогда и только тогда, когда
постовская система соответствия
является бесконечным тогда и только тогда, когда
постовская система соответствия 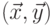 имеет решение.
имеет решение.
Теорема 16.3.11. Пусть  . Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом 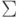 узнать, является ли бесконечным множество
узнать, является ли бесконечным множество 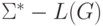 .
.
Упражнение 16.3.12. Рассмотрим язык, порождаемый грамматикой

Упражнение 16.3.13. Рассмотрим язык, порождаемый грамматикой