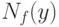|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Описание неопределенностей в теории принятия решений
Одна из ведущих научных школ в области анализа интервальных данных - это школа проф. А.П. Вощинина, активно работающая с конца 70-х годов. В частности, изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности.
Рассматриваемое ниже направление отличается нацеленностью на асимптотические результаты, полученные при больших объемах выборок и малых погрешностях измерений, поэтому оно и названо асимптотической статистикой интервальных данных.
Сформулируем сначала основные идеи асимптотической математической статистики интервальных данных. Следует сразу подчеркнуть, что основные идеи достаточно просты, в то время как их проработка в конкретных ситуациях зачастую оказывается достаточно трудоемкой.
Пусть существо реального явления описывается выборкой 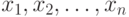 . В вероятностной теории математической статистики, из которой мы исходим, выборка - это набор n независимых в совокупности одинаково распределенных случайных величин. Однако беспристрастный и тщательный анализ подавляющего большинства реальных задач показывает, что статистику известна отнюдь не выборка
. В вероятностной теории математической статистики, из которой мы исходим, выборка - это набор n независимых в совокупности одинаково распределенных случайных величин. Однако беспристрастный и тщательный анализ подавляющего большинства реальных задач показывает, что статистику известна отнюдь не выборка 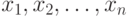 , а величины
, а величины
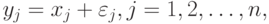
где 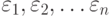 , некоторые погрешности измерений, наблюдений, анализов, опытов, исследований (например, инструментальные ошибки).
, некоторые погрешности измерений, наблюдений, анализов, опытов, исследований (например, инструментальные ошибки).
Одна из причин появления погрешностей - запись результатов наблюдений с конечным числом значащих цифр. Дело в том, что для случайных величин с непрерывными функциями распределения событие, состоящее в попадании хотя бы одного элемента выборки в множество рациональных чисел, согласно правилам теории вероятностей имеет вероятность 0, а такими событиями в теории вероятностей принято пренебрегать. Поэтому при рассуждениях о выборках из обычно используемых распределений (нормального, логарифмически нормального, экспоненциального, равномерного, гамма - распределений, распределения Вейбулла-Гнеденко и т.п.) приходится принимать, что эти распределения имеют элементы исходной выборки 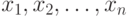 , в то время как статистической обработке доступны лишь искаженные значения
, в то время как статистической обработке доступны лишь искаженные значения  .
.
Введем обозначения
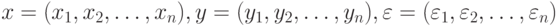
Пусть статистические выводы основываются на статистике  используемой для оценивания параметров и характеристик распределения, проверки гипотез и решения иных статистических задач. Принципиально важная для статистики интервальных данных идея такова: СТАТИСТИК ЗНАЕТ ТОЛЬКО
используемой для оценивания параметров и характеристик распределения, проверки гипотез и решения иных статистических задач. Принципиально важная для статистики интервальных данных идея такова: СТАТИСТИК ЗНАЕТ ТОЛЬКО 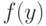 , НО НЕ
, НО НЕ 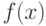 .
.
Очевидно, в статистических выводах необходимо отразить различие между 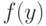 и
и 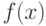 . Одним из двух основных понятий статистики интервальных данных является понятие нотны.
. Одним из двух основных понятий статистики интервальных данных является понятие нотны.
Определение. Величину максимально возможного (по абсолютной величине) отклонения, вызванного погрешностями наблюдений , известного статистику значения 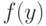 от истинного значения
от истинного значения 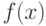 , т.е.
, т.е.
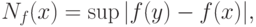
где супремум берется по множеству возможных значений вектора погрешностей  (см. ниже), будем называть НОТНОЙ .
(см. ниже), будем называть НОТНОЙ .
Если функция  имеет частные производные второго порядка, а ограничения на погрешности имеют вид
имеет частные производные второго порядка, а ограничения на погрешности имеют вид
 |
( 1) |
причем  мало, то приращение функции
мало, то приращение функции  с точностью до бесконечно малых более высокого порядка описывается главным линейным членом, т.е.
с точностью до бесконечно малых более высокого порядка описывается главным линейным членом, т.е.

Чтобы получить асимптотическое (при  ) выражение для нотны, достаточно найти максимум и минимум линейной функции (главного линейного члена) на кубе, заданном неравенствами (1).
) выражение для нотны, достаточно найти максимум и минимум линейной функции (главного линейного члена) на кубе, заданном неравенствами (1).
Легко видеть, что максимум достигается, если положить

а минимум, отличающийся от максимума только знаком, достигается при  . Следовательно, нотна с точностью до бесконечно малых более высокого порядка имеет вид
. Следовательно, нотна с точностью до бесконечно малых более высокого порядка имеет вид
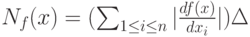
Это выражение назовем асимптотической нотной.
Условие (1) означает, что исходные данные представляются статистику в виде интервалов ![[y_i-\Delta; y_i+\Delta], i=1,2, \dots, n](/sites/default/files/tex_cache/8451a9e257fb2b3997fc5b1f82939fb6.png) (отсюда и название этого научного направления). Ограничения на погрешности могут задаваться разными способами - кроме абсолютных ошибок используются относительные или иные показатели различия между x и y.
(отсюда и название этого научного направления). Ограничения на погрешности могут задаваться разными способами - кроме абсолютных ошибок используются относительные или иные показатели различия между x и y.
Если задана не предельная абсолютная погрешность  , а предельная относительная погрешность
, а предельная относительная погрешность  , т.е. ограничения на погрешности вошедших в выборку результатов измерений имеют вид
, т.е. ограничения на погрешности вошедших в выборку результатов измерений имеют вид
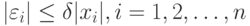
то аналогичным образом получаем, что нотна с точностью до бесконечно малых более высокого порядка, т.е. асимптотическая нотна, имеет вид

При практическом использовании рассматриваемой концепции необходимо провести в расчетных формулах тотальную замену символов x на символы y. В каждом конкретном случае удается показать, что в силу малости погрешностей разность 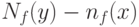 является бесконечно малой более высокого порядка сравнительно с
является бесконечно малой более высокого порядка сравнительно с 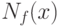 или
или