|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Основы эконометрических методов
Метод наименьших квадратов для линейной функции
Начнем с задачи точечного и доверительного оценивания линейной прогностической функции одной переменной.
Исходные данные - набор  пар чисел
пар чисел 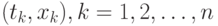 , где
, где 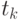 - независимая переменная (например, время), а
- независимая переменная (например, время), а 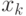 - зависимая (например, индекс инфляции, курс доллара США, объем месячного производства или размер дневной выручки торговой точки). Предполагается, что переменные связаны зависимостью
- зависимая (например, индекс инфляции, курс доллара США, объем месячного производства или размер дневной выручки торговой точки). Предполагается, что переменные связаны зависимостью
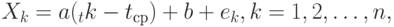
где  и
и  - параметры, неизвестные исследователю и подлежащие оцениванию, а
- параметры, неизвестные исследователю и подлежащие оцениванию, а 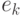 - погрешности, искажающие зависимость. Среднее арифметическое моментов времени
- погрешности, искажающие зависимость. Среднее арифметическое моментов времени
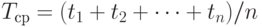
введено в модель для облегчения дальнейших выкладок.
Обычно оценивают параметры a и b линейной зависимости методом наименьших квадратов. Затем восстановленную зависимость используют для точечного и интервального прогнозирования.
Как известно, метод наименьших квадратов был разработан великим немецким математиком К. Гауссом в 1794 г. Согласно этому методу для расчета наилучшей функции, приближающей линейным образом зависимость  от
от  , следует рассмотреть функцию двух переменных
, следует рассмотреть функцию двух переменных
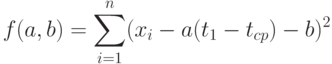
Оценки метода наименьших квадратов - это такие значения 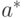 и
и 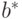 , при которых функция
, при которых функция 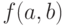 достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции
достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции 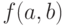 по аргументам
по аргументам  и
и  , приравнять их 0, затем из полученных уравнений найти оценки: Имеем:
, приравнять их 0, затем из полученных уравнений найти оценки: Имеем:
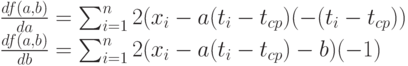
Преобразуем правые части полученных соотношений. Вынесем за знак суммы общие множители 2 и (-1). Затем рассмотрим слагаемые. Раскроем скобки в первом выражении, получим, что каждое слагаемое разбивается на три. Во втором выражении также каждое слагаемое есть сумма трех. Значит, каждая из сумм разбивается на три суммы. Имеем:
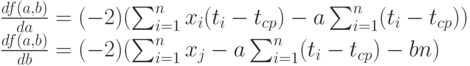
Приравняем частные производные 0. Тогда в полученных уравнениях можно сократить множитель (-2). Поскольку
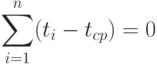 |
( 1) |
уравнения приобретают вид
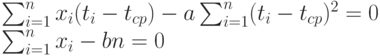
Следовательно, оценки метода наименьших квадратов имеют вид
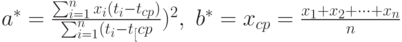 |
( 2) |
В силу соотношения (1) оценку 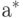 можно записать в более симметричном виде:
можно записать в более симметричном виде:
Эту оценку нетрудно преобразовать и к виду
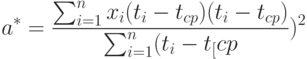 |
( 3) |
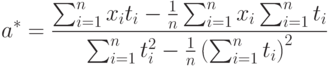 |
( 4) |
Следовательно, восстановленная функция, с помощью которой можно прогнозировать и интерполировать, имеет вид
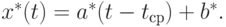
Обратим внимание на то, что использование 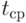 в последней формуле ничуть не ограничивает ее общность. Сравним с моделью вида
в последней формуле ничуть не ограничивает ее общность. Сравним с моделью вида
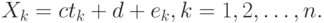
Ясно, что
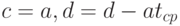
Аналогичным образом связаны оценки параметров:
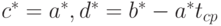
Для получения оценок параметров и прогностической формулы нет необходимости обращаться к какой-либо вероятностной модели. Однако для того, чтобы изучать погрешности оценок параметров и восстановленной функции, т.е. строить доверительные интервалы для 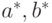 и
и 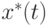 , подобная модель необходима.
, подобная модель необходима.
Непараметрическая вероятностная модель. Пусть значения независимой переменной  детерминированы, а погрешности
детерминированы, а погрешности 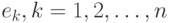 , - независимые одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией
, - независимые одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией 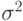 неизвестной исследователю.
неизвестной исследователю.
В дальнейшем неоднократно будем использовать Центральную Предельную Теорему (ЦПТ) теории вероятностей для величин 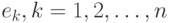 (с весами), поэтому для выполнения ее условий необходимо предположить, например, что погрешности
(с весами), поэтому для выполнения ее условий необходимо предположить, например, что погрешности 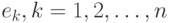 , финитны или имеют конечный третий абсолютный момент. Однако заострять внимание на этих внутриматематических "условиях регулярности" нет необходимости.
, финитны или имеют конечный третий абсолютный момент. Однако заострять внимание на этих внутриматематических "условиях регулярности" нет необходимости.
Асимптотические распределения оценок параметров. Из формулы (2) следует, что
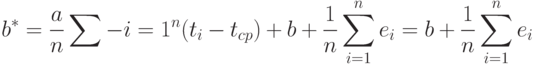 |
( 5) |
Согласно ЦПТ оценка 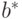 имеет асимптотически нормальное распределение с математическим ожиданием b и дисперсией
имеет асимптотически нормальное распределение с математическим ожиданием b и дисперсией 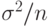 оценка которой приводится ниже.
оценка которой приводится ниже.
Из формул (2) и (5) вытекает, что
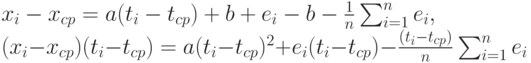
Последнее слагаемое во втором соотношении при суммировании по i обращается в 0, поэтому из формул (2-4) следует, что
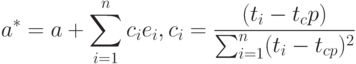 |
( 6) |
Формула (6) показывает, что оценка 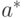 является асимптотически нормальной с математическим ожиданием
является асимптотически нормальной с математическим ожиданием 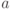 и дисперсией
и дисперсией
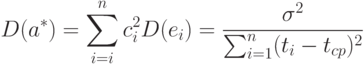
Отметим, что многомерная нормальность имеет быть, когда каждое слагаемое в формуле (6) мало сравнительно со всей суммой, т.е.
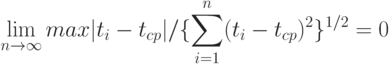
Из формул (5) и (6) и исходных предположений о погрешностях вытекает также несмещенность оценок параметров.
Несмещенность и асимптотическая нормальность оценок метода наименьших квадратов позволяют легко указывать для них асимптотические доверительные границы (аналогично границам в предыдущей главе) и проверять статистические гипотезы, например, о равенстве определенным значениям, прежде всего 0.

