Единственность главного ступенчатого вида матрицы
Изоморфизм линейных пространств
Пусть K U, K V - линейные пространства над полем K. Биективное отображение


 ,
, 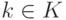 , называется изоморфизмом линейных пространств K U и K V (в этом случае будем говорить, что линейные пространства K U и K V изоморфны, обозначение:
, называется изоморфизмом линейных пространств K U и K V (в этом случае будем говорить, что линейные пространства K U и K V изоморфны, обозначение:  ).
).Упражнение 9.6.1. Отношение 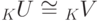 является отношением эквивалентности.
является отношением эквивалентности.
Лемма 9.6.2. Если  - изоморфизм линейных пространств,
- изоморфизм линейных пространств,  , {e1,...,en} - базис в K U, то {f(e1),...,f(en)} - базис в K V, и поэтому
, {e1,...,en} - базис в K U, то {f(e1),...,f(en)} - базис в K V, и поэтому  .
.
- 1) Если
 , то f(u)=v для некоторого
, то f(u)=v для некоторого 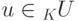 . Пусть u=k1e1+...+knen, где
. Пусть u=k1e1+...+knen, где 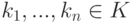 . Тогда v=f(u)=k1f(e1)+...+knf(en).
. Тогда v=f(u)=k1f(e1)+...+knf(en). - Пусть k_1f(e1)+...+knf(en)=0 для
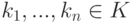 . Тогда 0=k1f(e1)+...+knf(en)=f(k1e1+...+knen),
и поэтому k1e11+...+knen=0, следовательно, k1=k2=...=kn=0.
. Тогда 0=k1f(e1)+...+knf(en)=f(k1e1+...+knen),
и поэтому k1e11+...+knen=0, следовательно, k1=k2=...=kn=0.Итак, в силу 1) и 2), {f(e1),...,f(en)} - базис линейного пространства KV.
Лемма 9.6.3. Если  и {e1,...,en} - базис линейного пространства K V, то, сопоставляя каждому элементу
и {e1,...,en} - базис линейного пространства K V, то, сопоставляя каждому элементу  однозначно определенную строчку его координат (k1,...,kn) в базисе {e1,...,en}, получаем изоморфизм линейных пространств
однозначно определенную строчку его координат (k1,...,kn) в базисе {e1,...,en}, получаем изоморфизм линейных пространств  , таким образом, каждое n -мерное линейное пространство K V над полем K изоморфно линейному пространству строк Kn.
, таким образом, каждое n -мерное линейное пространство K V над полем K изоморфно линейному пространству строк Kn.
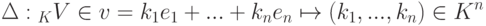

Теорема 9.6.4. Конечномерные линейные пространства K U и K V изоморфны тогда и только тогда, когда  , и в этом случае
, и в этом случае  .
.
Доказательство теоремы следует из лемм 9.6.2 и 9.6.3.
Упражнение 9.6.5. Покажите, что следующие линейные пространства являются бесконечномерными линейными пространствами (это означает, что в них нет базиса из конечного числа элементов):
- R C[0,1] - линейное пространство вещественных непрерывных функций на отрезке [0,1] ;
- K K[x] - линейное пространство многочленов от переменной x с коэффициентами из поля K ;
- K KN - линейное пространство всех счетных последовательностей (k1,k2,...,kn,...) элементов из поля K.
Упражнение 9.6.6. Докажите, что
а)  ;
;
б) 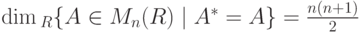 ;
;
в)  .
.

