Комбинаторика разбиений
Введение
В задачах, которые мы сейчас рассмотрим, элементы делятся на группы, и надо найти все способы такого раздела. При этом могут встретиться различные случаи. Иногда существенную роль играет порядок элементов в группах: например, когда сигнальщик вывешивает сигнальные флаги на нескольких мачтах, то для него важно не только то, на какой мачте окажется тот или иной флаг, но и то, в каком порядке эти флаги развешиваются. В других же случаях порядок элементов в группах никакой роли не играет. Когда игрок в домино выбирает кости из кучи, ему безразлично, в каком порядке они придут, а важен лишь окончательный результат.
Отличаются задачи и по тому, играет ли роль порядок самих групп. При игре в домино игроки сидят в определенном порядке, и важно не только то, как разделились кости, но и то, кому какие кости достались. Если раскладывать фотографии по одинаковым конвертам, чтобы разослать их, то существенно, как распределяются фотографии по конвертам, но порядок самих конвертов совершенно несущественен.
Играет роль и то, различаем ли мы между собой сами элементы или нет, а также различаем ли между собой группы, на которые делятся элементы. Наконец, в одних задачах некоторые группы могут оказаться пустыми, то есть не содержащими ни одного элемента, а в других такие группы недопустимы. В соответствии со всем сказанным возникает целый ряд различных комбинаторных задач на разбиение.
Задачи
Общая постановка этих задач:
Задача 1. Раскладка по ящикам
Даны  различных предметов и
различных предметов и  ящиков. Надо положить
в первый ящик
ящиков. Надо положить
в первый ящик 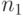 предметов, во второй
-
предметов, во второй
- 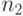 предметов,..., в
предметов,..., в  -й
-
-й
- 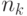 предметов, где
предметов, где 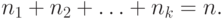 Сколькими способами можно сделать такое распределение?
Сколькими способами можно сделать такое распределение?
Число различных раскладок по ящикам равно

Задача 2. Перестановки с повторением.
Имеются предметы  различных типов. Сколько различных
перестановок можно сделать из
различных типов. Сколько различных
перестановок можно сделать из 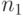 предметов первого
типа,
предметов первого
типа, 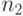 предметов второго типа, ...,
предметов второго типа, ..., 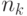 предметов
предметов  -го типа? Число элементов в каждой
перестановке равно
-го типа? Число элементов в каждой
перестановке равно 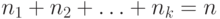 .
Поэтому если бы все элементы были различны, то число перестановок равнялось бы
.
Поэтому если бы все элементы были различны, то число перестановок равнялось бы  ! .
Но из-за того, что некоторые элементы совпадают, получится меньшее число
перестановок. В самом деле, возьмем, например, перестановку
! .
Но из-за того, что некоторые элементы совпадают, получится меньшее число
перестановок. В самом деле, возьмем, например, перестановку
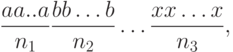 |
( 5.1) |
 -го типа. Элементы первого типа
можно переставлять друг с другом
-го типа. Элементы первого типа
можно переставлять друг с другом 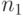 ! способами. Но так как все эти
элементы одинаковы, то такие перестановки ничего не
меняют. Точно так же ничего не меняют
! способами. Но так как все эти
элементы одинаковы, то такие перестановки ничего не
меняют. Точно так же ничего не меняют 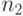 ! перестановок элементов
второго типа, ...,
! перестановок элементов
второго типа, ..., 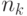 ! перестановок элементов
! перестановок элементов  -го типа.
-го типа.Перестановки элементов первого типа, второго типа и так далее можно делать
независимо друг от друга. Поэтому элементы перестановки 5.1. можно
переставлять друг с другом 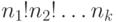 ! способами так, что она
остается неизменной. То же самое верно и для любого другого
расположения элементов. Поэтому множество всех
! способами так, что она
остается неизменной. То же самое верно и для любого другого
расположения элементов. Поэтому множество всех  ! перестановок
распадается на части, состоящие из
! перестановок
распадается на части, состоящие из 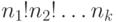 ! одинаковых перестановок каждая. Значит, число различных перестановок с
повторениями, которые можно сделать из данных элементов, равно
! одинаковых перестановок каждая. Значит, число различных перестановок с
повторениями, которые можно сделать из данных элементов, равно
 |
( 5.2) |
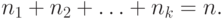
Пользуясь формулой 5.2, можно ответить на вопрос: сколько перестановок можно сделать из букв слова "Миссисипи"? Здесь у нас одна буква "м", четыре буквы "и", три буквы "с" и одна буква "п", а всего 9 букв. Значит, по формуле 5.2 число перестановок равно
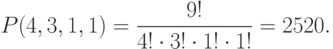
 мест,
которые могут занимать наши предметы. Каждой перестановке соответствует
распределение номеров мест на
мест,
которые могут занимать наши предметы. Каждой перестановке соответствует
распределение номеров мест на  классов. В первый класс попадают
номера тех мест, на которые попали предметы
первого типа, во второй - номера мест предметов второго типа и так далее. Тем
самым устанавливается соответствие между перестановками с повторениями и
раскладкой номеров мест по "ящикам". Понятно, что формулы решения
задач оказались одинаковыми.
классов. В первый класс попадают
номера тех мест, на которые попали предметы
первого типа, во второй - номера мест предметов второго типа и так далее. Тем
самым устанавливается соответствие между перестановками с повторениями и
раскладкой номеров мест по "ящикам". Понятно, что формулы решения
задач оказались одинаковыми.В рассмотренных задачах мы не учитывали порядок, в котором расположены элементы каждой части. В некоторых задачах этот порядок надо учитывать.
Задача 3. Флаги на мачтах.
Имеется  различных сигнальных флагов и
различных сигнальных флагов и  мачт, на
которые их вывешивают. Значение сигнала зависит от того, в каком
порядке развешены флаги. Сколькими способами можно развесить флаги, если все
флаги должны быть использованы, но некоторые из мачт могут оказаться
пустыми?
мачт, на
которые их вывешивают. Значение сигнала зависит от того, в каком
порядке развешены флаги. Сколькими способами можно развесить флаги, если все
флаги должны быть использованы, но некоторые из мачт могут оказаться
пустыми?
Каждый способ развешивания флагов можно осуществить в два этапа. На
первом этапе мы переставляем всеми возможными способами
данные  флагов. Это можно сделать
флагов. Это можно сделать  ! способами. Затем
берем один из способов распределения
! способами. Затем
берем один из способов распределения  одинаковых флагов
по
одинаковых флагов
по  мачтам (число этих способов
мачтам (число этих способов 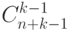 ).
Пусть этот способ заключается в
том, что на первую мачту надо повесить
).
Пусть этот способ заключается в
том, что на первую мачту надо повесить 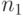 флагов, на вторую
-
флагов, на вторую
- 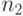 флагов, ..., на
флагов, ..., на  -ю
-ю 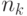 флагов,
где
флагов,
где 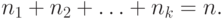 Тогда берем
первые
Тогда берем
первые 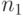 флагов данной последовательности и развешиваем в
полученном порядке на первой
мачте; следующие
флагов данной последовательности и развешиваем в
полученном порядке на первой
мачте; следующие 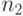 флагов развешиваем на второй мачте и т.д.
Ясно, что используя все перестановки
флагов развешиваем на второй мачте и т.д.
Ясно, что используя все перестановки  флагов и все способы
распределения
флагов и все способы
распределения  одинаковых флагов по
одинаковых флагов по  мачтам, получим
все способы решения поставленной задачи. По правилу произведения
получаем, что число способов развешивания флагов равно
мачтам, получим
все способы решения поставленной задачи. По правилу произведения
получаем, что число способов развешивания флагов равно
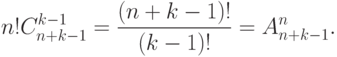 |
( 5.3) |
 различных вещей, то число способов распределения
этих вещей по
различных вещей, то число способов распределения
этих вещей по  различным ящикам равно
различным ящикам равно 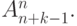
Разные статистики
Задачи о раскладке предметов по ящикам весьма важны для статистической
физики. Эта наука изучает, как распределяются по своим свойствам физические
частицы; например, какая часть молекул данного газа имеет при данной
температуре ту или иную скорость. При этом множество всех возможных состояний распределяют на
большое число  маленьких ячеек (фазовых состояний), так что каждая
из
маленьких ячеек (фазовых состояний), так что каждая
из  частиц попадет в одну из ячеек.
частиц попадет в одну из ячеек.
Вопрос о том, какой статистике подчиняются те или иные частицы, зависит от
вида этих частиц. В классической статистической физике, созданной Максвеллом и
Больцманом, частицы считаются различимыми друг от друга. Такой статистике
подчиняются, например, молекулы газа. Известно, что  различных
частиц можно распределить по
различных
частиц можно распределить по  ячейкам
ячейкам 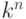 способами.
Если все эти
способами.
Если все эти 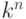 способов при заданной энергии имеют равную
вероятность, то говорят о статистике Максвелла-Больцмана.
способов при заданной энергии имеют равную
вероятность, то говорят о статистике Максвелла-Больцмана.
Оказалось, что этой статистике подчиняются не все физические объекты. Фотоны, атомные ядра и атомы, содержащие четное число элементарных частиц, подчиняются иной статистике, разработанной Эйнштейном и индийским ученым Бозе. В статистике Бозе-Эйнштейна частицы считаются неразличимыми друг от друга. Поэтому имеет значение лишь то, сколько частиц попало в ту или иную ячейку, а не то, какие именно частицы туда попали.
Однако для многих частиц, например таких как электроны, протоны и
нейтроны, не годится и статистика Бозе-Эйнштейна. Для них в каждой ячейке может
находится не более одной частицы, причем различные распределения,
удовлетворяющие указанному условию, имеют равную вероятность. В этом случае
может быть 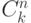 различных распределений. Эта статистика называется статистикой Дирака-Ферми.
различных распределений. Эта статистика называется статистикой Дирака-Ферми.
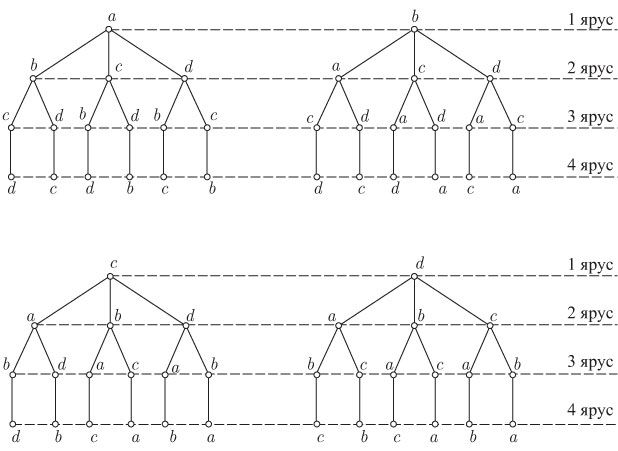
Деревья и перестановки из n элементов
С помощью леса можно представить перестановки из  элементов
множества
элементов
множества 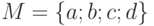 (множество мы определяем так: множество
- это неупорядоченная совокупность различных объектов или структура данных,
используемая для представления множества). Подсчитаем, сколько можно
получить перестановок. Для
(множество мы определяем так: множество
- это неупорядоченная совокупность различных объектов или структура данных,
используемая для представления множества). Подсчитаем, сколько можно
получить перестановок. Для  такой лес изображен на
рис. 5.1.
такой лес изображен на
рис. 5.1.