Рисование графических примитивов средствами GDI+

Упражнение 5. Рисование домика ломаными линиями

Для практики приведем еще один пример кода рисования ломаных. На этот раз нарисуем домик. Как и в предыдущем коде, воспользуемся собственным базовым классом PrintableForm.

using System;
using System.Drawing;
using System.Windows.Forms;
  
namespace Test
{
  public class DrawHouse : PrintableForm
  {
    public DrawHouse()
    {
      this.Text = "Рисование домика функцией DrawLines()";
    }
  
    // Перегруженная функция базового класса PrintableForm
    protected override void DoPage(Graphics graphics, Color color, int cx, int cy)
    {
      Point[] apoint = {
                new Point(cx / 4, 3 * cy / 4),
                new Point(cx / 4, cy / 2),
                new Point(cx / 2, cy / 4),
                new Point(3 * cx / 4, cy / 2),
                new Point(3 * cx / 4, 3 * cy / 4),
                new Point(cx / 4, cy / 2),
                new Point(3 * cx / 4, cy / 2),
                new Point(cx / 4, 3 * cy / 4),
                new Point(3 * cx / 4, 3 * cy / 4),
               };
      graphics.DrawLines(new Pen(color), apoint);
    }
  }
}

Результатом работы кода будет

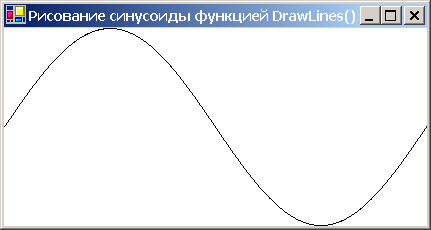
Упражнение 6. Применение функции DrawLines() для рисования графиков (рисование синусоиды)

Метод DrawLines() позволяет настраивать тип пера так, чтобы для толстых перьев получать нужные формы линий в местах соединения ломаных (закругленные, угловые и т.д.). Эти элементы линий называются концами или соединениями. Чтобы придать концам правильный вид, GDI+ должен знать, какими являются линии, имеющие общие точки: отдельными или соединенными. Об этом можно сообщить GDI+, используя метод DrawLines() вместо DrawLine().

Метод DrawLines() имеет очень большую производительность. Он создан не для рисования прямых, а для аппроксимации кривых, заданных математически. Даже если передать DrawLines() миллион структур Point или PointF, их визуализация будет мгновенной. Максимальная гладкость кривой достигается, если число ее точек по крайней мере равно числу пикселов. Для примера нарисуем один цикл синусоиды, вписанной в клиентскую область формы.

using System;
using System.Drawing;
using System.Windows.Forms;
  
namespace Test
{
  public class SineCurve : PrintableForm
  {
    public SineCurve()
    {
      this.Text = "Рисование синусоиды функцией DrawLines()";
    }
  
    // Перегруженная функция базового класса PrintableForm
    protected override void DoPage(Graphics graphics, Color color, int cx, int cy)
    {
      PointF[] apointf = new PointF[cx];
      for(int i = 0; i < cx; i++)
      {
        apointf[i].X = i;
        apointf[i].Y = ((float)(cy - 1) / 2) * (float)
          (1 - Math.Sin(i * 2 * Math.PI / (cx - 1)));
      }
      graphics.DrawLines(new Pen(color), apointf);
    }
  }
}

Здесь мы используем в качестве базового наш класс PrintableForm, и переопределяем в нем виртуальный метод DoPage(), задающий суть выводимой информации. Для вычисления синуса используется класс System.Math сборки mscorlib.lib. Большинство методов класса Math возвращает значение типа Double, которые нужно явно привести к типу float (структура System.Single сборки mscorlib.lib ). Отметим, что преобразование целого к вещественному является безопасным, поскольку не приведет к потере значений целого, поэтому можно преобразовать неявно и компилятор это воспринимает нормально.

Аргумент функции Math.Sin() задается в радианах. Полный круг ( 360^o ) соответствует 2*Pi радиан. Здесь у нас cx=ClientSize.Width, cy=ClientSize.Height. Таким образом, аргумент может принимать значения от 0 (когда i=0) до 2*Pi (когда i=cx). Значение метода Math.Sin() находится в интервале (-1,+1), поэтому его нужно умножить на полувысоту клиентской области. Полученные значения будут изменяться в интервале (-cy/2,+cy/2). Затем их нужно вычесть из половины высоты клиентской области, чтобы результат варьировался в диапазоне (0,cy).

Экран с результатом выполнения выглядит так

Метод DrawPolygon() класса Graphics отличается от DrawLines() тем, что автоматически замыкает первую и последнюю точки рисования.