Графы с цветными ребрами
Задачи на графы с цветными ребрами и вытекающие из них свойства
Рассматриваем графы, соответствующие таким ситуациям, в которых одни пары элементов множества находятся между собой в одном отношении, другие пары этого множества — в другом отношении, третьи — в третьем, но каждая пара — в одном отношении. Например, среди участников шахматного турнира к какому-то моменту могут быть такие, которые уже сыграли партию друг с другом, и такие, которые не сыграли. Среди множества стран есть страны, установившие между собой дипломатические связи, и страны, между которыми не установлены дипломатические связи. Для удобства на рисунках графов ребра, соответствующие одному отношению, окрашивают в один цвет, а ребра, соответствующие другому отношению, — во второй цвет, в третий цвет и т.д. Так как мы не можем выполнить рисунок в разных цветах, то присваиваем ребрам номера. Такие графы называются графами с цветными ребрами.
Свойства полных графов с цветными ребрами
Задача 1. Шесть человек участвуют в шахматном турнире, который проводится в один круг, то есть каждый шахматист встречается со всеми участниками по одному разу. Нужно доказать, что среди них всегда найдутся три участника турнира, которые провели уже все встречи между собой или еще не сыграли друг с другом ни одной партии.
Решение. Любые два участника турнира находятся между собой в одном из двух отношений: они либо уже сыграли между собой, либо еще не сыграли.
Каждому участнику поставим в соответствие вершину графа. Соединим вершины попарно ребрами двух цветов. Пусть ребро красного цвета (обозначенное цифрой 1) означает, что двое уже сыграли между собой, а синего (пронумерованное цифрой 2) — что не сыграли. Получим полный граф с шестью вершинами и ребрами двух цветов.
Теперь для решения задачи достаточно доказать, что в таком графе обязательно найдется "треугольник" с одноцветными сторонами.
Каждая вершина полученного графа принадлежит пяти ребрам. Скольким
шахматистам одного цвета может принадлежать произвольная вершина такого
графа? Пять принадлежащих одной вершине ребер могут быть окрашены без
учета порядка следующим образом: 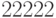 ,
,  ,
, 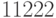 ,
, 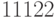 ,
,  ,
,  .
То есть каждая вершина принадлежит, по меньшей мере, трем шахматистам
одного цвета. Пусть, например, вершина
.
То есть каждая вершина принадлежит, по меньшей мере, трем шахматистам
одного цвета. Пусть, например, вершина 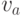 принадлежит трем
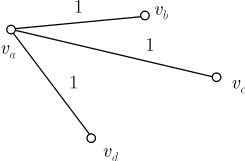
ребрам красного цвета:
принадлежит трем
ребрам красного цвета:
Какого цвета ребра могут соединять вершины 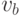 ,
, 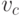 и
и 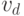 ?
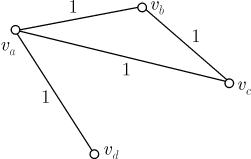
Если хотя бы одно из них окажется красным, как на рисунке,
?
Если хотя бы одно из них окажется красным, как на рисунке,
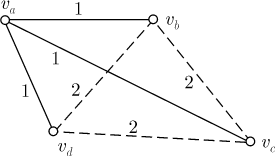
то получится треугольник с красными сторонами. Если же все эти ребра синие, как на рисунке,
то они вместе образуют "треугольник" с синими сторонами.
Задача решена. Рассмотрены все возможности. В каждом случае нашлись три шахматиста, или все сыгравшие между собой по одной партии, или не сыгравшие между собой ни одной партии.