|
Добрый день! Подскажите пожалуйста как и когда получить диплом, после сдичи и оплаты????? |
Введение в основы современных шифров с симметричным ключом
Составные шифры
Шеннон ввел понятие составные шифры. Составной шифр – комплекс, который объединяет подстановку, перестановку и другие компоненты, рассмотренные в предыдущих разделах.
Рассеивание и перемешивание
Идея Шеннона в представлении составного шифра должна была дать возможность блочным шифрам иметь две важных свойства: рассеяние и перемешивание. Рассеивание должно скрыть отношения между зашифрованным текстом и исходным текстом. Это собьет с толку противника, который использует статистику зашифрованного текста, чтобы найти исходный текст. Рассеивание подразумевает, что каждый символ (символ или бит) в зашифрованном тексте зависит от одного или всех символов в исходном тексте. Другими словами, если единственный символ в исходном тексте изменен, несколько или все символы в зашифрованном тексте будут также изменены.
Идея относительно перемешивания — в том, что оно должно скрыть отношения между зашифрованным текстом и ключом. Это собьет с толку противника, который стремится использовать зашифрованный текст, чтобы найти ключ. Другими словами, если единственный бит в ключе изменен, все биты в зашифрованном тексте будут также изменены.
Раунды
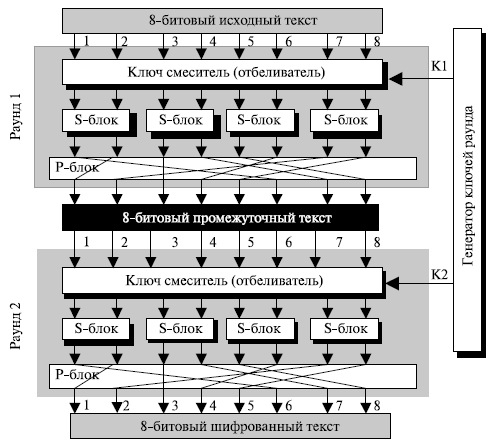
Распыление и перемешивание могут быть достигнуты использованием повторения составных шифров, где каждая итерация — комбинация S -блоков, P -блоков и других компонентов. Каждая итерация называется раундом.Блочный шифр использует ключевой список,или генератор ключей, который создает различные ключи для каждого раунда от ключа шифра. В N -раундном шифре, чтобы создать зашифрованный текст, исходный текст шифруется N раз; соответственно, зашифрованный текст расшифровывается N раз. Текст, созданный на промежуточных уровнях (между двумя раундами), называется средним текстом.Рисунок 7.13 показывает простой составной шифр с двумя раундами. На практике составные шифры имеют больше чем два раунда. На рис. 7.13 в каждом раунде проводятся три преобразования:
а. 8 -битовый текст смешивается с ключом, чтобы сделать символы текста равновероятными (скрыть биты, используя ключ) — "отбелить" текст (whiting). Это обычно делается с помощью операции ИСКЛЮЧАЮЩЕЕ ИЛИ слова на 8 битов с ключом на 8 битов.
б. Выходы "отбеливателя" разбиты на четыре группы по 2 бита и подаются в четыре S -блока. Значения битов изменяются в соответствии с построением S -блоков в этом преобразовании.
c. Выходы S -блоков поступают в P -блок, при этом биты переставлены так, чтобы в следующем раунде результат каждого блока поступил на различные входы.
Рассеивание, которое показано на упрощенном рис. 7.13 как составной шифр, используя комбинацию S -блоков и P -блоков, может гарантировать рассеивание.
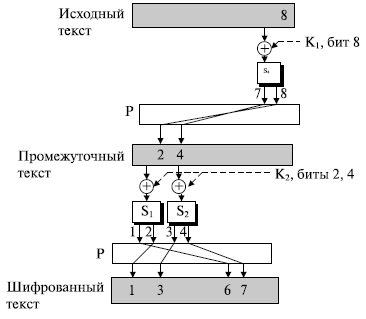
а. В первом раунде бит 8, после проведения операции ИСКЛЮЧАЮЩЕЕ ИЛИ с соответствующими битами ключа K1, изменяет два бита (биты 7 и 8 ) через S -блок 4. Бит 7 переставлен и становится битом 2 ; бит 8 переставлен и становится битом 4. После первого раунда бит 8 изменяет биты 2 и 4. Во втором раунде бит 2 после проведения операции ИСКЛЮЧАЮЩЕЕ ИЛИ с соответствующими битами ключа K2 изменяет два бита (биты 1 и 2 ) через S -блок 1. Бит 1 – переставлен и становится битом 6 ; бит 2 переставлен и становится битом 1. Бит 4 после проведения операции ИСКЛЮЧАЮЩЕЕ ИЛИ с соответствующим битом в K2 изменяет биты 3 и 4. Бит 3 остается, бит 4 переставлен и становится битом 7. После второго раунда из 8 бит изменены биты 1, 3, 6 и 7.
b. Прохождение этих шагов в другом направлении (от зашифрованного текста до исходного текста) показывает, что каждый бит в зашифрованном тексте изменяет исходный текст на несколько битов.
Перемешивание. На рисунке 7.14 показано, как изменение единственного бита в исходном тексте вызывает изменение многих битов в зашифрованном тексте. Рисунок 7.14 также доказывает нам, что свойство перемешивания может быть получено с помощью составного шифра. Четыре бита зашифрованного текста, биты 1, 3, 6 и 7 преобразованы с помощью трех битов в ключах (бит 8 в K1 и битах 2 и 4 в K2 ). Прохождение в обратном направлении показывает, что каждый бит ключа в каждом раунде затрагивает несколько битов в зашифрованном тексте. Отношения между битами зашифрованного текста и ключевыми битами показаны в затененных прямоугольниках.
Практические шифры. Чтобы улучшить рассеивание и перемешивание, практические шифры используют крупные блоки данных, больше S -блоков и больше раундов. Очевидно, что некоторое увеличение числа раундов при использовании большого числа S -блоков может создать лучший шифр, в котором зашифрованный текст выглядит все более как случайное n -битовое слово. Таким образом, отношения между зашифрованным текстом и исходным текстом будут полностью скрыты (рассеяны). Увеличение числа раундов увеличивает число ключей раундов, что лучше скрывает отношения между зашифрованным текстом и ключом.
Два класса составных шифров
Современные блочные шифры — все составные, но они разделены на два класса. Шифры в первом классе используют и обратимые, и необратимые компоненты. Эти шифры упоминаются обычно как шифры Файстеля. Блочный шифр DES (DATA ENCRYPTION STANDARD), обсуждаемый в "Шифрование, использующее современные шифры с симметричным ключом" , — хороший пример шифра Файстеля. Шифры во втором классе применяют только обратимые компоненты. Обращаем ваше внимание на шифры в этом классе как шифры не-Файстеля (из-за отсутствия другого названия). Блочный шифр AES (ADVANCED ENCRYPTION STANDARD), обсуждаемый в лекциях 12-13, — хороший пример шифра не-Файстеля.
Шифры Файстеля
Файстель проектировал очень интеллектуальный и интересный шифр, который использовался в течение многих десятилетий. Шифр Файстеля может иметь три типа компонентов: самообратимый, обратимый и необратимый.
Шифр Файстеля содержит в блоках все необратимые элементы и использует один и тот же модуль в алгоритмах дешифрования и шифрования. Вопрос в том, как алгоритмы шифрования и дешифрования позволяют инвертировать открытый и закрытый тексты друг в друга, если каждый содержит необратимый модуль. Файстель показал, что они могут быть сбалансированы.
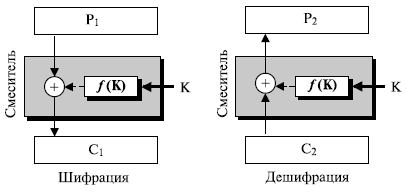
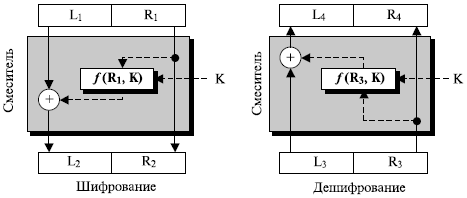
Первая идея. Чтобы лучше понять шифр Файстеля, давайте посмотрим, как мы можем использовать один и тот же необратимый компонент в алгоритмах дешифрования и шифрования. Эффекты необратимого компонента в алгоритме шифрования могут быть отменены в алгоритме дешифрования, если мы используем операцию ИСКЛЮЧАЮЩЕЕ ИЛИ, как показано на рис. 7.15.
В шифровании ключ поступает на вход необратимой функции f (K), которая является одним из слагаемых оператора ИСКЛЮЧАЮЩЕГО ИЛИ с исходным текстом. Результат становится зашифрованным текстом. Мы будем называть комбинацию функции и операции ИСКЛЮЧАЮЩЕЕ ИЛИ смесителем (из-за отсутствия другого названия). Смеситель играет важную роль в более поздних вариантах шифра Файстеля.
Поскольку ключ один и тот же в шифровании и дешифровании, мы можем доказать, что два алгоритма инверсны друг другу. Другими словами, если C2 = C1 (любое изменение в зашифрованном тексте в течение передачи), то P2 = P1.

Обратите внимание, что использовались два свойства операции ИСКЛЮЧАЮЩЕЕ ИЛИ (существование инверсии и существование нулевого кода).
Уравнения, показанные выше, доказывают, что хотя смеситель имеет неконвертируемый элемент, сам смеситель является самоконвертируемым.
Пример 7.12
Это тривиальный пример. Имеется исходный текст и зашифрованный текст, каждый 4 бита длиной, и ключ 3 бита длиной. Предположим, что функция извлекает первый и третий биты ключа, интерпретирует биты как десятичный номер, находит квадрат этого числа и интерпретирует результат как 4 -битовую двоичную последовательность. Покажите результаты шифрования и дешифрования, если первоначальный исходный текст — 0111, и ключ — 101.
Решение
Функция извлекает первые и третьи биты ключа и получается в результате 11 в двоичном виде или 3 в десятичном отображении. Результат возведения во вторую степень (квадрат) — 9, в двоичном отображении 1001.
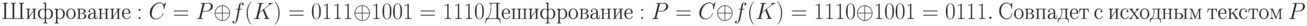
Функция f (101) = 1001 является неконвертируемой, но операция ИСКЛЮЧАЮЩЕЕ ИЛИ позволяет нам использовать функцию и в алгоритмах дешифрования, и в шифровании. Другими словами, функция является неконвертируемой, но смеситель будет самоконвертируемым.
Усовершенствование. Попробуем улучшить нашу первую идею, чтобы приблизиться к шифру Файстеля. Мы знаем, что должны применить вход к неконвертируемому элементу (функции), но мы не будем использовать только ключ. Мы задействуем также вход к функции, чтобы применить ее для шифрования части исходного текста и дешифрования части зашифрованного текста. Ключ может использоваться как второй вход к функции. Этим способом наша функция становится сложным элементом с некоторыми неключевыми элементами и некоторыми ключевыми элементами. Чтобы достичь цели, разделим исходный текст и зашифрованный текст на два блока равной длины – левый ( L ) и правый ( R ). Правый блок вводится в функцию, а левый блок складывается с помощью операции ИСКЛЮЧАЮЩЕЕ ИЛИ с выходом функции. Мы должны запомнить, что входы к функции должны точно совпадать в шифровании и дешифровании. Это означает, что правая секция исходного текста до шифрования и правая секция зашифрованного текста после дешифрования будут совпадать. Другими словами, секция должна войти в шифрование и выйти из дешифрования неизмененной. Рисунок 7.16 иллюстрирует идею.
Алгоритмы шифрование и дешифрования инверсны друг другу. Предположим, что L3 = L2 и R3 = R2 (в зашифрованном тексте в течение передачи не произошло изменений).
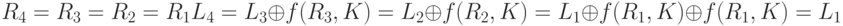
Исходный текст, используемый в алгоритме шифрования, — это текст, правильно восстановленный алгоритмом дешифрования.
Окончательный вариант. Предыдущее усовершенствование имеет один недостаток: правая половина исходного текста никогда не изменяется. Ева может немедленно найти правую половину исходного текста, разбивая на части зашифрованный текст и распаковывая его правую половину. Проект нуждается в дальнейших шагах усовершенствования.
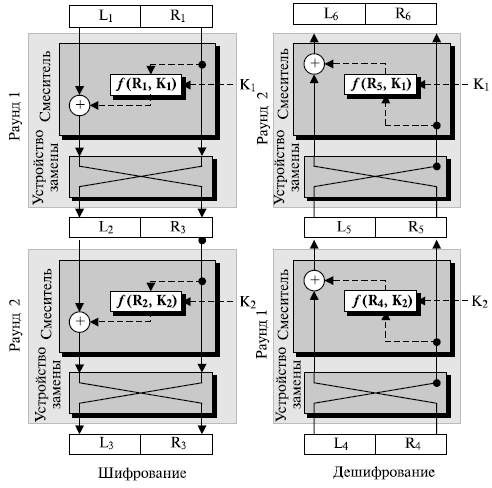
Первое: увеличим число раундов. Второе: добавим новый элемент в каждый раунд — устройство замены. Эффект устройства замены в раунде шифрования компенсируется эффектом устройства замены в раунде дешифрования. Однако это позволяет нам менять левые и правые половины в каждом раунде. Рисунок 7.17 иллюстрирует новый вариант шифра Файстеля с двумя раундами.
Обратите внимание, что есть два ключа раундов: K1 и K2. Ключи используются в обратном порядке в шифровании и дешифровании.
Поскольку два смесителя инверсны друг другу и устройства замены инверсны друг другу, очевидно, что шифрование и дешифрование также инверсны друг другу. Однако мы можем доказать этот факт, используя отношения между левыми и правыми секциями в каждом шифре. Другими словами, если L6 = L1 и R6 = R1, предположим, что L4 = L3 и R4 = R3 (шифрованный текст не изменился при передаче). Вначале докажем это для промежуточного текста:
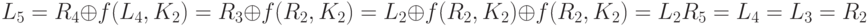
Тогда просто доказать равенство для двух блоков исходного текста.
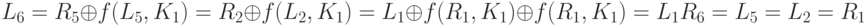
Шифры не-Файстеля
Шифр не-Файстеля использует только обратимые компоненты. Компонент в исходном тексте имеет соответствующий компонент в шифре. Например, S -блоки должны иметь равное число входов и выходов, чтобы быть совместимыми. Не позволяется никакое сжатие или расширение P -блоков, потому что они станут необратимыми. В шифре не-Файстеля нет потребности делить исходный текст на две половины, как мы видели в шифрах Файстеля.
Рисунок 7.13 можно рассматривать как графическую иллюстрацию принципа шифра не-Файстеля, потому что единственные компоненты в каждом раунде — самообратимые операции ИСКЛЮЧАЮЩЕЕ ИЛИ, S -блоки  , которые могут спроектированы, чтобы быть обратимыми, и прямые P -блоки, которые обратимы, если использована соответствующая таблица перестановки. Поскольку каждый компонент является обратимым, то можно показать, что и каждый раунд является обратимым. Мы только должны применять ключи раундов в обратном порядке. Шифрование использует ключи раундов K1 и K2. Алгоритм дешифрования должен пользоваться ключами раундов K2 и K1.
, которые могут спроектированы, чтобы быть обратимыми, и прямые P -блоки, которые обратимы, если использована соответствующая таблица перестановки. Поскольку каждый компонент является обратимым, то можно показать, что и каждый раунд является обратимым. Мы только должны применять ключи раундов в обратном порядке. Шифрование использует ключи раундов K1 и K2. Алгоритм дешифрования должен пользоваться ключами раундов K2 и K1.