НОУ ИНТУИТ | Прикладная статистика. Лекция 10: Статистика временных рядов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Доступ: свободный | Студентов: 4093 / 1040 | Оценка: 4.66 / 4.45 | Длительность: 54:13:00

Темы: Математика, Экономика

Специальности: Экономист

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

10.4. Моделирование и анализ многомерных временных рядов

Рассмотрим методы моделирования и анализа многомерных временных рядов, используемых для изучения реальных процессов взаимовлияния факторов на основе подхода ЖОК, описанного в 10.3.

Основные сведения о системе ЖОК. Компьютерная система ЖОК - это система поддержки анализа и управления в сложных ситуациях^{1Использованы разработки В.Н.Жихарева, выполненные в Институте высоких статистических технологий и эконометрики.}, описываемых многомерными временными рядами. Она предназначена для структуризации и анализа сложных, трудно формализуемых, слабо структурированных задач различной природы (экономической, управленческой, прогностической, технической, медицинской, социально-политической, экологической и пр.). Она применяется для построения моделей ситуаций на основе описания влияний факторов. Это делается с помощью ориентированных графов и использования оценок экспертов с последующим определением наиболее эффективных управленческих решений. Компьютерная система ЖОК:

поддерживает аналитическое обоснование подходов к решению исследуемых проблем;
позволяет спрогнозировать развитие моделируемой реальной системы; оценить результаты целенаправленного изменения тех или иных факторов;
дает возможность выработать условия для целенаправленного поведения в исследуемой ситуации;
обеспечивает возможность решения прямых и обратных задач управления.

Для построения модели изучаемого явления или процесса компьютерная система ЖОК предусматривает выделение основных факторов, описывающих реальную ситуацию, и установление непосредственных взаимосвязей между факторами в виде построения ориентированного взвешенного графа. Опосредованные взаимовлияния и итоговое стационарное состояние рассчитываются по описанным ниже алгоритмам. Система позволяет анализировать три основных типа сценариев:

"Прогноз", позволяющий проследить "естественное" развитие моделируемой системы при отсутствии активных воздействий;
"Активный", при котором работающий с системой специалист изменяет значения тех или иных параметров и анализирует получающуюся динамику и итоговое состояние (например, с целью ручного поиска рационального управления);
"Цель", когда компьютерная система по заданной цели управления (например, значения определенных параметров должны быть не менее заданных) находит оптимальные воздействия путем решения соответствующей задачи оптимизации. В частности, проводит анализ принципиальной достижимости указанной цели из текущего состояния с использованием выбранных мероприятий (управлений).

Ядром компьютерной системы ЖОК является описанная ниже математическая модель. Преобразование задач анализа реальных явлений и процессов к математической постановке, оценка адекватности реальности и ее модели, процесс выбора управлений, процесс сравнительного анализа различных ситуаций в целом, моделирования и последующей интерпретации результатов математического моделирования относится к области "ручного труда" специалиста в соответствующей области знания и полной автоматизации, как правило, не поддается.

Компьютерная система ЖОК обеспечивает расчет равновесного (стационарного) состояния, к которому будет стремиться система взаимовлияющих факторов, и всех промежуточных состояний на пути от начального состояния к равновесному. В систему включены три варианта расчетов:

равновесного состояния без управления (учитываются только начальные данные);
равновесного состояния с управлением импульсного типа (при t = 0). (В такой модели система интерпретирует импульсное управление, как поправку к начальным данным.);
величины управления по заданным значениям величины приращения целевых факторов.

Математические алгоритмы исследовательской системы ЖОК. Используются следующие обозначения:

- количество вершин в ориентированном графе модели, т.е. число используемых в модели факторов;
$D=\left[d_{i,j}\right]_{n\times n}$ - матрица порядка $n\times n$ непосредственных влияний факторов (матрица смежности графа );
$D^T=A=\left[a_{i,j}\right]_{n\times n}$ - матрица, транспонированная к матрице (называемая матрицей непосредственных контрвлияний факторов);
- время, принимающее дискретные значения 0, 1, 2, 3, ...;
вектор 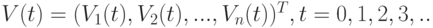., - вектор изменений (приращений, дифференциалов) факторов в момент дискретного времени ;
вектор $W(t)=\Delta V(t)=V(t)-V(t-1), t = 0, 1, 2, 3, ..$ ., является вектором дифференциалов факторов второго порядка в момент дискретного времени ;
вектор 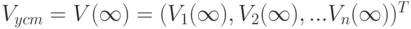$V_{ycm}=V(\infty)=(V_1(\infty),V_2(\infty),...V_n(\infty))^T$ обозначает величины предельных стационарных изменений (дифференциалов) факторов при безграничном росте . (Очевидно, что если $V(\infty)$ существует, то
$W(\infty)=\Delta V(\infty)=\lim_{n\rightarrow\infty}(V(t)-V(t-1))=0 ;$
вектор обозначает внешние управляющие воздействия, подаваемые на фактор 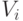в момент ;
вектор - сравнительную важность факторов 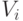, задаваемую экспертным путем;
вектор 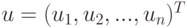- отношение составителя модели к направлению изменения величин факторов 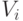(+1 - рост значения фактора оценивается положительно, (-1) - отрицательно, 0 - нейтрально);

- единичная $n\times n$ матрица (на главной диагонали стоят 1, на остальных позициях - 0);

- прореженная единичная $n\times n$ матрица, в которой единицы стоят на диагонали только на тех позициях, которые соответствуют целевым факторам. Очевидно, что является проектором на координатную плоскость целевых факторов, и следовательно C^2 = C , матрица является псевдообратной к матрице ;

- прореженная единичная $n\times n$ матрица, в которой единицы стоят на диагонали только на тех позициях, которые соответствуют управляющим факторам. Очевидно, что является проектором на координатную плоскость управляющих факторов, и, следовательно B^2 = B , матрица является псевдообратной к матрице ;

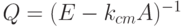$Q=(E-k_{cm}A)^{-1}$ - резольвента, где $k_{cm}$ - множитель-стабилизатор, который используется в целях обеспечения достаточно устойчивой и быстрой сходимости итерационного процесса приближенного вычисления матрицы резольвентного оператора

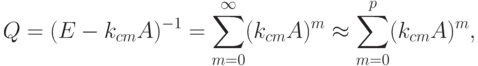
$Q=(E-k_{cm}A)^{-1}=\sum_{m=0}^{\infty}(k_{cm}A)^m\approx \sum_{m=0}^p(k_{cm}A)^m,$

где

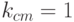достаточно велико. Полагают $k_{cm}=1$ в том случае, если собственные числа матрицы

достаточно малы (обычно принимается, что $k_{cm}A$ должна иметь собственные числа не только меньше единицы, но и меньше 0,9). Поскольку стабилизатор $k_{cm}$ имеет лишь внутриматематический смысл и не используется при построении модели и интерпретации результатов расчетов, то в дальнейшем его не будем упоминать, предполагая по умолчанию $k_{cm}=1$ .

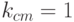Система уравнений в математико-статистической модели. Для описания динамики факторов в компьютерной системе ЖОК используется математико-статистическая модель в виде системы линейных конечноразностных рекуррентных уравнений на трехточечном шаблоне 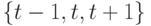$\{t-1, t, t+1\}$ следующего вида:

$\begin{aligned} V_i(t+1)&=V_i(t)+\sum_{j=1}^n a_{i,j}(V_j(t)-V_j(t-1))+g_i(t)= \\ &=V_i(t)+\sum_{j=1}^n d_{j,i}(V_j(t)-V_j(t-1))+g_i(t) \end{aligned}$

( 1)

с начальными условиями

( 2)

где

.

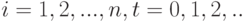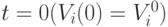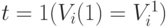Для рекуррентного уравнения на трехточечном шаблоне необходимо задать начальные условия при t = 0 (V_i(0)=V_i^0) и t = 1(V_i(1)=V_i^1) . Следовательно, первым уравнением цепочки рекуррентных уравнений (1) будет уравнение при t = 1 .

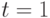При 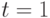t = 1 уравнение полагается определенным и имеет вид

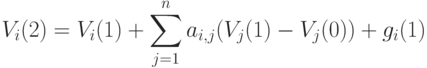
$V_i(2)=V_i(1)+\sum_{j=1}^n a_{i,j}(V_j(1)-V_j(0))+g_i(1)$

Для 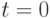t = 0 уравнение определяется посредством соотношения

( 3)

и тогда недостающие начальные данные V_i=V_i^1

вычисляются из уравнения

$V_i(1)=V_i(0)+\sum_{j=1}^n a_{i,j}(V_j(0)-V_j(-1))+g_i(0)=V_i(0)+\sum_{j=1}^n a_{i,j}V_j(0)+g_i(0)$

( 4)

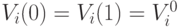Заметим, что доопределение начальных данных V_i(-1)=0 (нулем) - всего лишь один из способов. В частности, если положить V_i(0)=V_i(1)=V_i^0 , то результаты вычислений будут другими.

Из уравнений (1) видно, что используемая модель предполагает, что за один шаг дискретного времени $(\Delta t = 1)$ происходит распространение влияния факторов-аргументов только на непосредственно от них зависящие факторы-функции. Времени можно придать содержательный смысл, если за шаг принять реальный интервал времени, необходимый для осуществления непосредственного влияния одного фактора на другой. Этот интервал может быть оценен экспертно, В ряде случаев его можно принять равным кварталу.

Уравнение (1) - (2) в векторной форме имеет вид

$V(t+1)=V(t)+A\circ(V(t)-V(t-1))+g(t)$

( 5)

( 6)

где

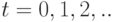.. Решение задачи (5) - (6) определяется формулой

$V(t)=V(0)+\left(\sum_{k=0}^t A^k\right)\circ V(0)+\sum_{k=0}^{t-1}\sum_{m=0}^{t-1-k}A^m\circ B\circ g(k).$

( 7)

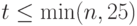Стационарное состояние и начальные условия. Стационарное состояние $V(\infty)$ вычисляется приближенно при $t\rightarrow\infty$ . Для практических расчетов достаточно принять, что $t\le\min(n,25)$ .

Векторное уравнение (5) может быть представлено в виде уравнения для дифференциалов второго порядка:

$W(t+1)=A\circ W(t)+g(t)$

( 8)

$W(0)=\Delta V(0)=V(0)-V(-1)=V(0),$

( 9)

где

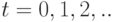. Решение уравнения (8) - (9) имеет вид

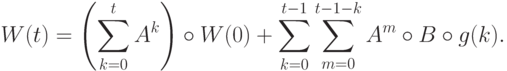$W(t)=\left(\sum_{k=0}^t A^k\right)\circ W(0)+\sum_{k=0}^{t-1}\sum_{m=0}^{t-1-k}A^m\circ B\circ g(k).$

( 10)

Если просуммировать уравнения (8) при 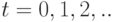t = 0, 1, 2, .. . , то получим (при условии сходимости)

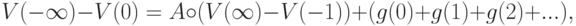$V(-\infty)-V(0)=A\circ(V(\infty)-V(-1))+(g(0)+g(1)+g(2)+...),$

( 11)

откуда следует

$V(\infty)=(E-A)^{-1}\circ(V(0)+g(0)+g(1)+g(2)+...)$

( 12)

Если же просуммировать уравнения (8) при t = 1, 2, .. ., то получим (при условии сходимости)

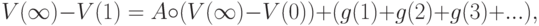$V(\infty)-V(1)=A\circ(V(\infty)-V(0))+(g(1)+g(2)+g(3)+...),$

( 13)

и соответственно

$V(\infty)=V(0)+(E-A)^{-1}\circ(V(1)-V(0))+(g(1)+g(2)+g(3)+...),$

( 14)

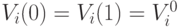откуда видно, что при выборе начальных условий вида V_i(0)=V_i(1)=V_i^0

результат (14) отличается от (12).

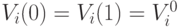В частности, при выборе режима прогноза развития ситуации без управления g(1)=g(2)=g(3)=...=0 и выборе начальных условий V_i(0)=V_i(1)=V_i^0 , которые выражают равенство нулю вторых производных от величин факторов при 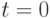t = 0 , из формулы (14) получим 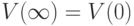$V(\infty)=V(0)$ . Это означает, что никакого развития ситуации не происходит. Она продолжает двигаться "равномерно и прямолинейно", поскольку вторые дифференциалы факторов равны нулю и первые дифференциалы факторов не изменяются во времени.

С другой стороны, формула (12) предполагает, что начальные данные оказывают такое же ударное воздействие в момент 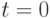t = 0 , как и внешнее импульсное при 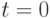t = 0 управление, играющее роль (и имеющее "размерность") "механической силы".

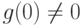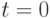Если предполагается использование только импульсных управляющих воздействий $g(0)\ne 0$ при t = 0 и в дальнейшем g(1)=g(2)=g(3)=...=0 , то задача развития ситуации без управления и с управлением не отличаются друг от друга, поскольку управление в сущности играет роль поправки к начальным данным и, обратно, начальные данные выполняют роль поправки к управлению.

Режим поиска управления по целевым значениям факторов. Проекция стационарного решения (12) уравнения (8) - (9) на координатную плоскость целевых факторов может быть представлено в виде

$Y_{ycm}=Y(V(0))+Y(g(0)),$

где

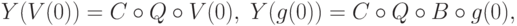
$Y(V(0))=C\circ Q\circ V(0),\; Y(g(0))=C\circ Q\circ B\circ g(0),$

или иначе

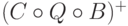$Y_{ycm}=C\circ Q\circ V(0)+C\circ Q\circ B\circ g(0)= C\circ Q\circ(V(0)+B\circ g(0)).$

( 15)

Пусть $Y_{ycm}^*$ - вектор значений дифференциалов целевых факторов, тогда импульсное управление g(0) определяется по формуле

$g(0)=(C\circ Q\circ B)^+\circ(Y_{ycm}^*-C\circ Q\circ V(0)),$

( 16)

где "+" обозначает операцию псевдоинверсии, и матрица $(C\circ Q\circ B)^+$ является псевдообратной к матрице $C\circ Q\circ B$ ;

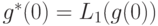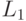g^*(0)=L_1(g(0)) является результатом применения к вектору g(0) операции L_1 - ограничения числовых значений компонент вектора g(0) величинами +1 и -1, если эти значения выходят за пределы отрезка [-1; +1];

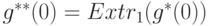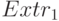$g^{**}(0)=Extr_1(g^*(0))$ получается из g^*(0) применением операции Extr_1 - замены числовых значений g^*(0) ближайшими к ним экстремальными на отрезке [-1; +1] величинами +1 или -1 соответственно.

Тогда стационарные решения, получаемые с использованием этих управлений, вычисляются по формулам

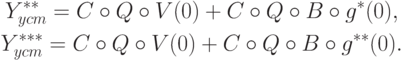
$\begin{gathered} Y_{ycm}^{**}=C\circ Q\circ V(0)+C\circ Q\circ B\circ g^*(0), \\ Y_{ycm}^{***}=C\circ Q\circ V(0)+C\circ Q\circ B\circ g^{**}(0). \end{gathered}$

Степени матрицы смежности графа и опосредованные взаимовлияния факторов. Пусть вершина 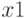влияет на вершину с силой 0,5, вершина влияет на с силой 0,6, вершина 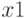влияет на 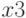с силой 0,8, вершина 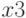влияет на с силой 0,4. Тогда опосредованное суммарное влияние 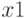на имеет силу

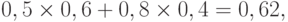
$0,5\times 0,6 + 0,8\times 0,4 = 0,62,$

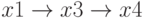что равно сумме весов двух путей $x1 \rightarrow x2 \rightarrow x4$ и $x1 \rightarrow x3 \rightarrow x4$ из

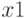в

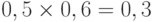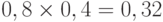, веса которых равны соответственно $0,5\times 0,6 = 0,3$ и $0,8\times 0,4 = 0,32$ . Суммарная сила влияния одного фактора на другой равна сумме весов всех маршрутов в ориентированном графе

, ведущих из одного фактора в другой. Вес пути (маршрута) определяется как произведение весов дуг составляющих этот путь (маршрут).

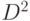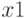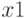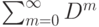Если рассмотреть степени матрицы $D=\left[d_{i,j}\right]{n\times n}$ , то их элементам можно придать вполне определенный смысл. Так, например, элемент матрицы D^2 с координатами (1,2) равен сумме весов всех маршрутов из в , содержащих ровно две дуги, а в D^3 сумме весов всех маршрутов из в , содержащих ровно три дуги и т.д. 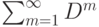Таким образом, матрица $\sum_{m=0}^{\infty}D^m$ выражает суммарные опосредованные влияния факторов друг на друга с учетом рефлексивного (при m = 0 ) непосредственного влияния фактора на самое себя с силой +1, а матрица $\sum_{m=1}^{\infty}D^m$ не учитывает рефлексивного непосредственного влияния.

Матрица 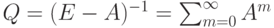$Q=(E-A)^{-1}=\sum_{m=0}^{\infty}A^m$ является матрицей контрвлияний факторов с учетом рефлексивности, а матрица $Q-E=-E+\sum_{m=0}^{\infty}A^m=\sum_{m=1}^{\infty}A^m=A\circ \sum_{m=0}^{\infty}A^m=A\circ Q=A\circ(E-A)^{-1}$ - матрицей контрвлияний факторов без учета рефлексивности.

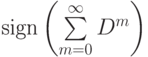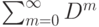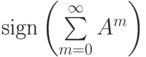Отдельный интерес представляет собой матрица $\text{sign}\left(\sum\limits_{m=0}^{\infty}D^m\right)$ знаков элементов матрицы $\sum_{m=0}^{\infty}D^m$ , т.е. матрица направленности интегральных влияний фактора на фактор (или контрвлияний, если рассмотреть матрицу $\text{sign}\left(\sum\limits_{m=0}^{\infty}A^m\right)$ ).

Дальше >>

Авторизоваться

Прикладная статистика

Статистика временных рядов

10.4. Моделирование и анализ многомерных временных рядов

Вопросы и ответы