|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Теоретическая база прикладной статистики
4.5. Принцип инвариантности
Пусть 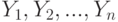 - независимые одинаково распределенные случайные величины с непрерывной функцией распределения
- независимые одинаково распределенные случайные величины с непрерывной функцией распределения 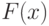 . Многие используемые в прикладной статистике функции от результатов наблюдений выражаются через эмпирическую функцию распределения
. Многие используемые в прикладной статистике функции от результатов наблюдений выражаются через эмпирическую функцию распределения 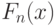 . К ним относятся статистики Колмогорова, Смирнова, омега-квадрат. Отметим, что и другие статистики выражаются через эмпирическую функцию распределения, например:
. К ним относятся статистики Колмогорова, Смирнова, омега-квадрат. Отметим, что и другие статистики выражаются через эмпирическую функцию распределения, например:
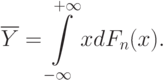
Полезным является преобразование Н.В.Смирнова 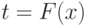 . Тогда независимые случайные величины
. Тогда независимые случайные величины 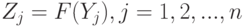 , имеют равномерное распределение на отрезке [0; 1]. Рассмотрим построенную по ним эмпирическую функцию распределения
, имеют равномерное распределение на отрезке [0; 1]. Рассмотрим построенную по ним эмпирическую функцию распределения 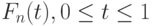 . Эмпирическим процессом называется случайный процесс
. Эмпирическим процессом называется случайный процесс
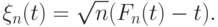
Рассмотрим критерии проверки согласия функции распределения выборки с фиксированной функцией распределения 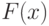 . Статистика критерия Колмогорова записывается в виде
. Статистика критерия Колмогорова записывается в виде
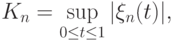
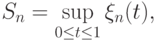
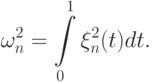
Случайный процесс 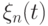 имеет нулевое математическое ожидание и ковариационную функцию
имеет нулевое математическое ожидание и ковариационную функцию 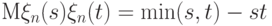 . Рассмотрим гауссовский случайный процесс
. Рассмотрим гауссовский случайный процесс  с такими же математическим ожиданием и ковариационной функцией. Он называется броуновским мостом. (Напомним, что гауссовским процесс именуется потому, что вектор
с такими же математическим ожиданием и ковариационной функцией. Он называется броуновским мостом. (Напомним, что гауссовским процесс именуется потому, что вектор 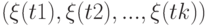 имеет многомерное нормальное распределение при любых наборах моментов времени
имеет многомерное нормальное распределение при любых наборах моментов времени 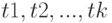 .)
.)
Пусть  - функционал, определенный на множестве возможных траекторий случайных процессов. Принцип инвариантности [
[
4.4
]
] состоит в том, что последовательность распределений случайных величин
- функционал, определенный на множестве возможных траекторий случайных процессов. Принцип инвариантности [
[
4.4
]
] состоит в том, что последовательность распределений случайных величин 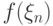 сходится при
сходится при 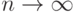 к распределению случайной величины
к распределению случайной величины 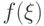 . Сходимость по распределению обозначим символом
. Сходимость по распределению обозначим символом  . Тогда принцип инвариантности кратко записывается так:
. Тогда принцип инвариантности кратко записывается так:  . В частности, согласно принципу инвариантности статистика Колмогорова и статистика омега квадрат сходятся по распределению к распределениям соответствующих функционалов от случайного процесса
. В частности, согласно принципу инвариантности статистика Колмогорова и статистика омега квадрат сходятся по распределению к распределениям соответствующих функционалов от случайного процесса  :
:
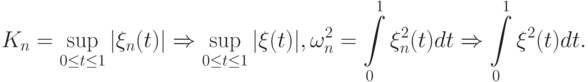
Таким образом, от проблем прикладной статистики сделан переход к теории случайных процессов. Методами этой теории найдены распределения случайных величин
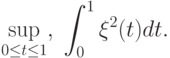
Принцип инвариантности - инструмент получения предельных распределений функций от результатов наблюдений, используемых в прикладной статистике.
Обоснование принципу инвариантности может быть дано на основе теории сходимости вероятностных мер в функциональных пространствах [ [ 4.1 ] ]. Более простой подход, позволяющий к тому же получать необходимые и достаточные условия в предельной теории статистик интегрального типа (принцип инвариантности к ним нельзя применить), рассмотрен в "Проверка гипотез" .
Почему "принцип инвариантности" так назван? Обратим внимание, что предельные распределения рассматриваемых статистик не зависят от их функции распределения 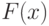 . Другими словами, предельное распределение инвариантно относительно выбора
. Другими словами, предельное распределение инвариантно относительно выбора 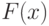 .
.
В более широком смысле термин "принцип инвариантности" применяют тогда, когда предельное распределение не зависит от тех или иных характеристик исходных распределений [ [ 4.4 ] ]. В этом смысле наиболее известный "принцип инвариантности" - это центральная предельная теорема, поскольку предельное стандартное нормальное распределение - одно и то же для всех возможных распределений независимых одинаково распределенных слагаемых (лишь бы слагаемые имели конечные математическое ожидание и дисперсию).
