|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Различные виды статистических данных
1.4. Нечеткие множества - частный случай нечисловых данных
Нечеткие множества. Пусть  - некоторое множество. Подмножество
- некоторое множество. Подмножество  множества
множества  может быть задано своей характеристической функцией
может быть задано своей характеристической функцией
 |
( 1) |
Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество  множества
множества  характеризуется своей функцией принадлежности
характеризуется своей функцией принадлежности ![\mu_C:A\rightarrow [0,1]](/sites/default/files/tex_cache/acec3f293cd75bc899a3dafcfd3ac7bf.png) . Значение функции принадлежности в точке
. Значение функции принадлежности в точке  показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х - она одновременно и входит, и не входит в нечеткое множество
показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х - она одновременно и входит, и не входит в нечеткое множество  . За вхождение -
. За вхождение - 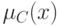 шансов, за второе -
шансов, за второе - 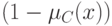 шансов.
шансов.
Если функция принадлежности 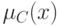 имеет вид (1) при некотором
имеет вид (1) при некотором  , то
, то  есть обычное (четкое) подмножество
есть обычное (четкое) подмножество  . Таким образом, теория нечетких множество является не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества - частный случай нечетких. Соответственно можно ожидать, что теория нечеткости, как целое, обобщает классическую математику. Однако позже мы увидим, что теория нечеткости в определенном смысле сводится к теории случайных множеств и тем самым является частью классической математики. Другими словами, по степени общности обычная математика и нечеткая математика эквивалентны. Однако для практического применения, например, в теории принятия решений описание и анализ неопределенностей с помощью теории нечетких множеств весьма плодотворны.
. Таким образом, теория нечетких множество является не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества - частный случай нечетких. Соответственно можно ожидать, что теория нечеткости, как целое, обобщает классическую математику. Однако позже мы увидим, что теория нечеткости в определенном смысле сводится к теории случайных множеств и тем самым является частью классической математики. Другими словами, по степени общности обычная математика и нечеткая математика эквивалентны. Однако для практического применения, например, в теории принятия решений описание и анализ неопределенностей с помощью теории нечетких множеств весьма плодотворны.
Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин "нечеткое подмножество" предпочтительнее при построении математических моделей реальных явлений.
Теория нечеткости является обобщением интервальной математики. Действительно, функция принадлежности
![\mu_B(x)=
\left \{
\begin{gathered}
1,x\in [a,b],\\
0,x\notin [a,b]
\end{gathered}
\right.](/sites/default/files/tex_cache/a9c87c5c92a92826125a008b05936101.png)
задает интервальную неопределенность - про рассматриваемую величину известно лишь, что она лежит в заданном интервале ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.
. Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.
Начало современной теории нечеткости положено в 1965 г. работой американского ученого азербайджанского происхождения Л.А. Заде. К настоящему времени по этой теории опубликованы тысячи книг и статей, издается несколько международных журналов, выполнено достаточно много как теоретических, так и прикладных работ. Первая книга российского автора по теории нечеткости вышла в 1980 г. [ [ 1.16 ] ].
Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от "принадлежности" к "непринадлежности" не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятиями, качеством продукции и технологическими процессами, при описании предпочтений потребителей и варки стали.
Л.А. Заде использовал термин "fuzzy set" (нечеткое множество). На русский язык термин "fuzzy" переводили как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный.
Аппарат теории нечеткости громоздок. В качестве примера дадим определения теоретико-множественных операций над нечеткими множествами. Пусть  и
и  - два нечетких подмножества
- два нечетких подмножества  с функциями принадлежности
с функциями принадлежности 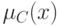 и
и 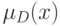 соответственно. Пересечением
соответственно. Пересечением 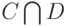 , произведением
, произведением 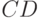 , объединением
, объединением 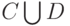 , отрицанием
, отрицанием 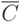 , суммой
, суммой 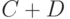 называются нечеткие подмножества
называются нечеткие подмножества  с функциями принадлежности
с функциями принадлежности
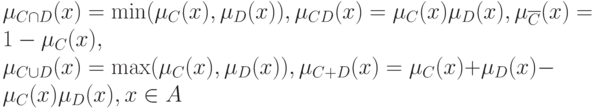
соответственно.
Как уже отмечалось, теория нечетких множеств в определенном смысле сводится к теории вероятностей, а именно, к теории случайных множеств. Соответствующий цикл теорем приведен ниже в "Теоретическая база прикладной статистики" . Однако при решении прикладных задач вероятностно-статистические методы и методы теории нечеткости обычно рассматриваются как различные.
Для знакомства со спецификой нечетких множеств рассмотрим некоторые их свойства.
В дальнейшем считаем, что все рассматриваемые нечеткие множества являются подмножествами одного и того же множества  .
.
Законы де Моргана для нечетких множеств. Как известно, законами де Моргана называются следующие тождества алгебры множеств
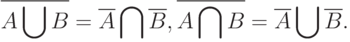 |
( 2) |
Теорема 1. Для нечетких множеств справедливы тождества
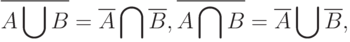 |
( 3) |
 |
( 4) |
Доказательство теоремы 1 состоит в непосредственной проверке справедливости соотношений (3) и (4) путем вычисления значений функций принадлежности участвующих в этих соотношениях нечетких множеств на основе определений, данных выше.
Тождества (3) и (4) назовем законами де Моргана для нечетких множеств. В отличие от классического случая соотношений (2), они состоят из четырех тождеств, одна пара которых относится к операциям объединения и пересечения, а вторая - к операциям произведения и суммы. Как и соотношение (2) в алгебре множеств, законы де Моргана в алгебре нечетких множеств позволяют преобразовывать выражения и формулы, в состав которых входят операции отрицания.
Дистрибутивный закон для нечетких множеств. Некоторые свойства операций над множествами не выполнены для нечетких множеств. Так, 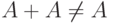 за исключением случая, когда
за исключением случая, когда  - "четкое" множество (т.е. функция принадлежности принимает только значения 0 и 1).
- "четкое" множество (т.е. функция принадлежности принимает только значения 0 и 1).
Верен ли дистрибутивный закон для нечетких множеств? В литературе иногда расплывчато утверждается, что "не всегда". Внесем полную ясность.
Теорема 2. Для любых нечетких множеств  ,
, 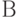 и
и 
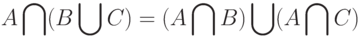 |
( 5) |
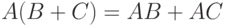 |
( 6) |
справедливо тогда и только тогда, когда при всех 
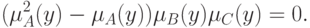
Доказательство. Фиксируем произвольный элемент  . Для сокращения записи обозначим
. Для сокращения записи обозначим 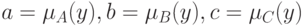 Для доказательства тождества (5) необходимо показать, что
Для доказательства тождества (5) необходимо показать, что
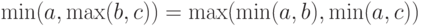 |
( 7) |
Рассмотрим различные упорядочения трех чисел 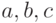 . Пусть сначала
. Пусть сначала  . Тогда левая часть соотношения (7) есть
. Тогда левая часть соотношения (7) есть 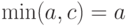 , а правая
, а правая 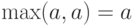 , т.е. равенство (7) справедливо.
, т.е. равенство (7) справедливо.
Пусть 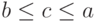 . Тогда в соотношении (7) слева стоит
. Тогда в соотношении (7) слева стоит 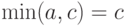 , а справа
, а справа 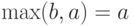 , т.е. соотношение (7) опять является равенством.
, т.е. соотношение (7) опять является равенством.
Если 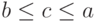 , то в соотношении (7) слева стоит
, то в соотношении (7) слева стоит 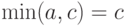 , а справа
, а справа 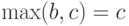 , т.е. обе части снова совпадают.
, т.е. обе части снова совпадают.
Три остальные упорядочения чисел 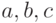 разбирать нет необходимости, поскольку в соотношение (6) числа
разбирать нет необходимости, поскольку в соотношение (6) числа  и
и  входят симметрично. Тождество (5) доказано.
входят симметрично. Тождество (5) доказано.
Второе утверждение теоремы 2 вытекает из того, что в соответствии с определениями операций над нечеткими множествами
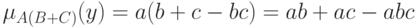
и
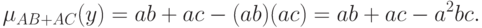
Эти два выражения совпадают тогда и только тогда, когда  , что и требовалось доказать.
, что и требовалось доказать.
Определение 1. Носителем нечеткого множества  называется совокупность всех точек
называется совокупность всех точек  , для которых
, для которых 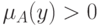 .
.
Следствие теоремы 2. Если носители нечетких множеств  и
и  совпадают с
совпадают с  , то равенство (6) имеет место тогда и только тогда, когда
, то равенство (6) имеет место тогда и только тогда, когда  - "четкое" (т.е. обычное, классическое, не нечеткое) множество.
- "четкое" (т.е. обычное, классическое, не нечеткое) множество.
Доказательство. По условию 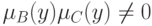 при всех
при всех  . Тогда из теоремы 2 следует, что
. Тогда из теоремы 2 следует, что  , т.е.
, т.е. 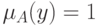 или
или 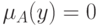 , что и означает, что
, что и означает, что  - четкое множество.
- четкое множество.
Пример описания неопределенности с помощью нечеткого множества. Понятие "богатый" часто используется при обсуждении социально-экономических проблем, в том числе и в связи с подготовкой и принятием решений. Однако очевидно, что разные лица вкладывают в это понятие различное содержание. Сотрудники Института высоких статистических технологий и эконометрики провели в 2004 г. небольшое пилотное социологическое исследование представления различных слоев населения о понятии "богатый человек".
Мини-анкета опроса выглядела так:
- При каком месячном доходе (в тыс. руб. на одного человека) Вы считали бы себя богатым человеком?
- Оценив свой сегодняшний доход, к какой из категорий Вы себя относите:
a) богатые;
б) достаток выше среднего;
в) достаток ниже среднего;
г) бедные;
д) за чертой бедности.
(В дальнейшем вместо полного наименования категорий будем оперировать буквами, например "в" - категория, "б" - категория и т.д.) - Ваша профессия, специальность.
