|
"...Изучение и анализ примеров.
В и приведены описания и приложены исходные коды параллельных программ..." Непонятно что такое - "В и приведены описания" и где именно приведены и приложены исходные коды. |
Спонсор: Microsoft
Вы можете этот курс.
Опубликован: 15.10.2009 | Доступ: свободный | Студентов: 896 / 248 | Оценка: 4.42 / 4.20 | Длительность: 08:22:00
Специальности: Программист
Теги:
Лекция 5:
Программирование с использованием Task Parallel Library (TPL)
Семинарское занятие № 5. Рекурсия и параллелизм (часть 2)
На предыдущем семинарском занятии было рассмотрено несколько методов рекурсивной параллельной обработки (бинарных) деревьев. Хотя последний из приведенных методов обладает достаточной степенью параллелизма, он имеет ряд серьезных недостатков:
- вызов метода Process в рамках потока из ThreadPool блокирует этот поток до тех пор, пока не будут обработаны вершины-потомки для данной вершины-родителя; таким образом, данная реализация требует одного потока из ThreadPool на одну вершину обрабатываемого дерева; однако, класс ThreadPool имеет ограниченное количество потоков, а именно 25 потоков на ядро (процессор) для .NET 1.x/2.0, и 250 потоков на процессор для .NET 2.0 SP1; таким образом, если из пула выбраны все потоки, то новые потоки не могут быть созданы, а потому приложение может перейти в состояние дедлока;
- создание нового потока в ThreadPool, когда количество уже созданных потоков больше или равно количеству доступных ядер (процессоров), занимает около 500 мсек; а потому обработка дерева, например, из 250 вершин займет более 2-х минут, потраченных только на создание потоков;
- для каждого вновь создаваемого потока в .NET отводится около 1 Мб (виртуальной) памяти;
- для обработки каждой вершины дерева создается один объект класса ManualResetEvent, операции над которым Set и WaitOne выполняются ядром операционной системы, а потому являются дорогостоящими в смысле используемых ресурсов.
Чтобы избавиться от некоторых из этих недостатков, ниже показана реализация, которая основана на последовательном проходе по дереву и записи в очередь на обработку в пул потоков задания на обработку каждой вершины в дереве.
public static void Process<T> (Tree<T> tree, Action<T> action)
{
if (tree == null) return;
// Использование события для ожидания завершения
// обработки всех вершин дерева
using (var mre = new ManualResetEvent(false))
{
int count = 1;
// Рекурсивный делегат для прохода по дереву
Action<Tree<T> > processNode = null;
processNode = node =>
{
if (node == null) return;
// Асинхронный запуск обработки текущей вершины
Interlocked.Increment(ref count);
ThreadPool.QueueUserWorkItem(delegate
{
action(node.Data);
if (Interlocked.Decrement(ref count) == 0)
mre.Set();
});
// Обработка потомков
processNode(node.Left);
processNode(node.Right);
};
// Запуск обработки, начиная с корневой вершины
processNode(tree);
// Сигнал о том, что заданий на обработку больше
// создаваться не будет
if (Interlocked.Decrement(ref count) == 0) mre.Set();
// Ожидание завершения обработки всех вершин
mre.WaitOne();
}
}
Пример
5.1.
Задача 5.
- Объясните почему данная реализация свободна от дедлоков в отличие от предыдущей реализации.
-
Объясните возможен ли вариант данной реализации, в котором исходным значением счетчика является 0, т.е.,
int count = 0;
а в методе Process последний оператор
if ( Interlocked.Decrement ( ref count ) == 0 ) mre.Set();
опущен.
Рекурсивный подход, приведенный в предыдущем примере, можно реализовать итеративно:
public static void Process<T> (Tree<T> tree, Action<T> action)
{
if (tree == null) return;
// Использование события для ожидания завершения
// обработки всех вершин дерева
using (var mre = new ManualResetEvent(false))
{
int count = 1;
// Запуск обработки, начиная с корневой вершины
var toExplore = new Stack<Tree<T> > ();
toExplore.Push(tree);
// Обработка всех вершин
while (toExplore.Count > 0)
{
// Извлечь текущую вершину и поместить в стек
// ее потомков
var current = toExplore.Pop();
if (current.Left != null)
toExplore.Push(current.Left);
if (current.Right != null)
toExplore.Push(current.Right);
// Асинхронная обработка данных
Interlocked.Increment(ref count);
ThreadPool.QueueUserWorkItem(delegate
{
action(current.Data);
if (Interlocked.Decrement(ref count) == 0)
mre.Set();
});
}
// Сигнал о том, что больше заданий на обработку
// создаваться не будет
if (Interlocked.Decrement(ref count) == 0) mre.Set();
// Ожидание завершения обработки всех верщин
mre.WaitOne();
}
}
Пример
5.2.
Недостаток предыдущего варианта состоит в том, что для каждой вершины дерева в ThreadPool помещается одно задание для обработки этой вершины. Гораздо экономичнее, а потому, эффективнее будет создать только 
заданий на обработку (где равно числу доступных процессоров на машине), и где каждое задание будет состоять в обработке примерно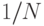 
-ой части всех вершин дерева. Такой подход можно реализовать, например, сохранив все вершины дерева в виде списка, и разделив его на частей, для обработки каждой части в виде параллельного задания:
public static void Process<T> (Tree<T> tree, Action<T> action)
{
if (tree == null) return;
// Создать список всех вершин дерева
var nodes = new List<Tree<T> > ();
var toExplore = new Stack<Tree<T> > ();
toExplore.Push(tree);
while (toExplore.Count > 0)
{
var current = toExplore.Pop();
nodes.Add(current);
if (current.Left != null)
toExplore.Push(current.Left);
if (current.Right != null)
toExplore.Push(current.Right);
}
// Разбиение списка на части
int workItems = Environment.ProcessorCount;
int chunkSize = Math.Max( nodes.Count / workItems, 1);
int count = workItems;
// Использование события для ожидания завершения
// обработки всех заданий
using (var mre = new ManualResetEvent(false))
{
// В каждом задании обрабатывается примерно 1/N-я
// часть вершин
WaitCallback callback = state =>
{
int iteration = (int)state;
int from = chunkSize * iteration;
int to = iteration == workItems - 1 ?
nodes.Count : chunkSize * (iteration + 1);
while (from < to) action(nodes[from++].Data);
if (Interlocked.Decrement(ref count) == 0)
mre.Set();
};
// ThreadPool используется для обработки N - 1 части;
// для обработки последней части используется
// текущий поток
for (int i = 0; i<workItems; i++)
{
if (i < workItems-1)
ThreadPool.QueueUserWorkItem(callback, i);
else
callback(i);
}
// Ожидание завершения обработки всех заданий
mre.WaitOne();
}
}
Пример
5.3.
Задача 6.
Проверьте, какой величины получатся задания для каждого процессора, если обрабатываемое дерево имеет 63 вершины, а количество процессоров равно 8.
Придумайте и реализуйте более оптимальный способ распределения вершин по заданиям, такой, чтобы размер любой пары заданий отличался не более, чем на 1.
Статическое разбиение списка на части также может быть не оптимальным способом деления работы между потоками. Альтернативным вариантом является динамическое разбиение, когда потоки конкурируют между собой за получение задания на обработку очередной вершины дерева после окончания обработки предыдущей вершины. Подход на основе динамического разбиения можно реализовать следующим способом:
public static void Process<T> (Tree<T> tree, Action<T> action)
{
if (tree == null) return;
// Получение конструкции перечисления для дерева
IEnumerator<T> enumerator =
GetNodes(tree).GetEnumerator();
int workItems = Environment.ProcessorCount;
int count = workItems;
// Использование события для ожидания завершения
// работы всех потоков
using (var mre = new ManualResetEvent(false))
{
// Каждый поток будет получать данные для обработки,
// используя механизм перечисления до тех пор,
// пока не будут исчерпаны все вершины дерева
WaitCallback callback = delegate
{
while (true)
{
T data;
lock (enumerator)
{
if (!enumerator.MoveNext()) break;
data = enumerator.Current;
}
action(data);
}
if (Interlocked.Decrement(ref count) == 0)
mre.Set();
};
// Из ThreadPool'а берется всего N - 1 потоков;
// кроме того, для обработки используется
// текущий поток
for (int i = 0; i < workItems; i++)
{
if (i < workItems-1)
ThreadPool.QueueUserWorkItem(callback, i);
else
callback(i);
}
// Ожидание завершения работы всех потоков
mre.WaitOne();
}
}
// Конструкция перечисления вершин дерева
public static IEnumerable<T> GetNodes<T> (Tree<T> tree)
{
if (tree != null)
{
yield return tree.Data;
foreach (var data in GetNodes(tree.Left))
yield return data;
foreach (var data in GetNodes(tree.Right))
yield return data;
}
}
Пример
5.4.
Недостаток последнего варианта состоит в том, что если обработка каждой вершины состоит из небольшого количества вычислительных операций, то общая производительность приложения будет низка из-за частого использования конструкции запирания lock. Поэтому, в некоторых случаях более оптимальным может оказаться вариант при котором при каждом применении lock к enumerator потоком извлекается сразу несколько вершин для обработки.
Задача 7.
Пусть для предыдущего примера дополнительным аргументом метода Process является целочисленный параметр 
, задающий количество вершин, извлекаемых из enumerator'а, при каждом применении к нему оператора lock. Реализуйте метод Process с указанным дополнением.
Возможны и некоторые другие способы распределения вершин (бинарного) дерева между потоками для обработки.
Задача 8.
Пусть 
есть количество доступных ядер/процессоров на машине. Предположим, что 
для некоторого 
. Напишите программу обработки всех вершин бинарного дерева, в которой главный поток сам обрабатывает все вершины дерева, начиная с корня, и до глубины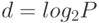 
, и порождает дополнительные потоки для обработки соответствующих поддеревьев на этой глубине.
Пример с обходом вершин дерева был достаточно прост в том смысле, что не требовалось блокировать обработку родительской вершины до тех пор, пока не будут обработаны ее вершины-потомки, и, наоборот, обработку вершин-потомков можно было начинать, не дожидаясь окончания обработки родительской вершины.
Однако, для многих рекурсивных задач такая автономная схема обработки невозможна. Рассмотрим, для примера, типичный рекурсивный алгоритм сортировки, а именно, алгоритм быстрой сортировки (дополнительную информацию об этом алгоритме можно найти на странице http://en.wikipedia.org/wiki/Quicksort):
public static void Quicksort<T> (T[] arr, int left, int right)
where T : IComparable <T>
{
if (right > left)
{
int pivot = Partition ( arr, left, right );
Quicksort ( arr, left, pivot - 1 );
Quicksort ( arr, pivot + 1, right );
}
}
Пример
5.5.
Из этого примера видно, что стартовать асинхронное выполнение вызовов Quicksort можно только после завершения шага Partition.
Задача 9.
Реализуйте параллельный вариант рекурсивного алгоритма Quicksort с помощью класса ThreadPool. Оцените количество порождаемых потоков при сортировке массивов большой длины. Придумайте способ увеличения эффективности данного алгоритма и реализуйте его.
Противоположная проблема, по сравнению с алгоритмом Quicksort, имеет место в рекурсивном варианте программы сортировки слиянием:
public static void Mergesort<T> (T[] arr, int left, int right)
where T : IComparable <T>
{
if (right > left)
{
int mid = ( right + left ) / 2;
Mergesort ( arr, left, mid );
Mergesort ( arr, mid + 1, right );
Merge ( arr, left, mid + 1, right );
}
}
Пример
5.6.
В этом варианте, мы получили алгоритм, аналогичный рассматривавшимся в семинаре к лекции 4. А именно - поток, выполняющий функцию Mergesort, блокируется перед выполнением шага Merge до тех пор, пока не будут (асинхронно) выполнены рекурсивные вызовы Mergesort. Другими словами, такой вид обработки очень трудно эффективно реализовать средствами класса ThreadPool.
Максим Полищук