|
Так это же динамическое программирование на основе математической индукции. |
Регулярные позиномы
В точке минимума компоненты ее производная обращается в нуль. Решим уравнения (например, с помощью надстройки Поиск решения (Solver) в Excel ):
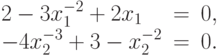
Для первой компоненты единственной стационарной точкой в области  является
является 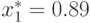 , следовательно,
, следовательно,

Для второй компоненты единственной стационарной точкой в области  является
является 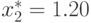 , следовательно,
, следовательно,

Верхняя оценка позинома равна

Таким образом, вычислив оценки, мы установили, что
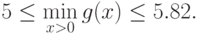
Заметим, что в данном примере верхняя оценка 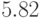 , достаточно
близка к минимальному значению позинома, которое равно
, достаточно
близка к минимальному значению позинома, которое равно 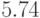 .
Разность составляет
.
Разность составляет
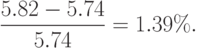
Рассмотрим еще один пример.
Пример 26 Вычислим оценки позинома из примера 9 ( "Неравенство Коши и его обобщения" ):
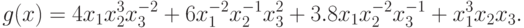
Вычислим сначала нижнюю оценку позинома. Для этого представим
второй моном 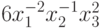 как сумму двух
мономов:
как сумму двух
мономов:
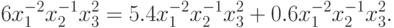
Теперь позином имеет вид:
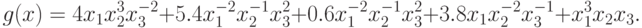
Возьмем ![S=[1, 2, 4 , 5]](/sites/default/files/tex_cache/3c9bbb13be9f24da5dbadd67140ba728.png) . Позином
. Позином
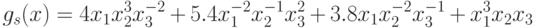
является регулярным, так как для него выполнены следующие равенства:
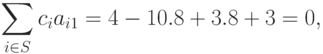
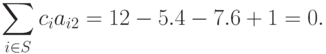
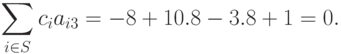
Следовательно, его минимум вычисляется по формуле:
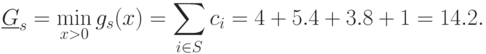
Таким образом, получили нижнюю оценку для позинома 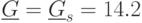 .
.
Вычислим теперь верхнюю оценку минимума позинома. Позином состоит из трех компонент:
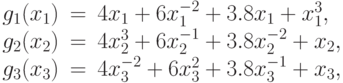
Вычислим минимумы компонент позинома. Для каждой компоненты запишем производную:
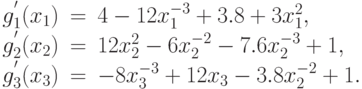
В точке минимума компоненты ее производная обращается в нуль. Решим уравнения (например, с помощью надстройки Поиск решения (Solver) в Excel ):
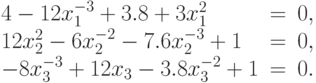
Для первой компоненты единственной стационарной точкой в области  является
является 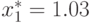 , следовательно,
, следовательно,
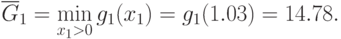
Для второй компоненты единственной стационарной точкой в области  является
является 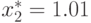 , следовательно,
, следовательно,
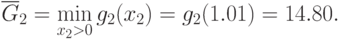
Для третьей компоненты единственной стационарной точкой в области  является
является 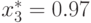 , следовательно,
, следовательно,
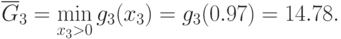
Верхняя оценка позинома равна
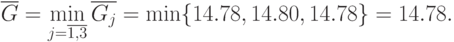
Таким образом, вычислив оценки, мы установили, что
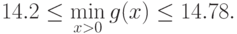
Заметим, что в данном примере верхняя оценка 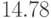 совпала с
минимальным значением позинома.
совпала с
минимальным значением позинома.
Краткие итоги
Введено понятие регулярного позинома. Описаны свойства регулярных позиномов. Приведена теорема минимизации регулярных позиномов. Сформулирована главная теорема о позиномах. Описан процесс вычисления оценки минимума позинома.
