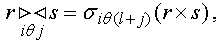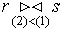Формализация реляционной модели
Пример 1.
Сформировать список студентов (фамилия).
Рассмотрим схему отношения СТУДЕНТ.
Атрибут "Фамилия" обозначен здесь А2 Для ответа на запрос необходимо взять проекцию отношения r1 на столбец А2.

Пример 2.
Выдать список фамилий и дат рождений студентов, которым на текущую дату (date) больше 35 лет.
Рассмотрим то же отношение r1. Сначала выбираем студентов, которым больше 35 лет:

Затем берем проекцию полученного отношения на столбцы

Заметим, что можно было бы выполнить эти две операции в другой последовательности – сначала проекция, а затем селекция. Предлагается оценить, какой из этих вариантов лучше по оценке числа выполняемых элементарных действий и объему требуемой памяти.
Пример 3.
Выдать список фамилий студентов, обучающихся по специальности "Информационные технологии". Название специальности является атрибутом отношения r3. Если бы в этом отношении присутствовал атрибут "фамилия", то задача решалась бы аналогично примеру 2. В отношении r5 присутствует атрибут "код студента", а "фамилия" присутствует в отношении r1. Для ответа на этот запрос необходимо связывать по "код студента" отношение r3 и отношение r1.
Сначала выберем из отношения r3 кортежи с названием специальности "Информационные технологии". Обозначим полученное отношение rp1. (Дальнейшие промежуточные отношения будем обозначать последовательно rp1, rp2, rp3 и т.д.).

Далее нас будет интересовать только атрибут A1 – "код студента". Поэтому возьмем проекцию на эти столбцы.
 .
.
Далее необходимо связать отношения r1 и rp2 (склеить таблицы). Для склейки таблиц используется операция "декартово произведение":
rp3=r1xrp2
В отношении r3 присутствуют два одинаковых столбца: A1 из отношения r1 и A1 из отношения rp2. Выбирая из отношения rp3 строки, в которых значения в соответствующих столбцах совпадают, получим сведения о студентах, обучающихся по специальности "Информационные технологии"
 ,
,
где A1 * r1 и A1 * rp2 обозначают соответственно столбец A1 соответствующей первой и второй составной части декартова произведения. Теперь осталось только выбрать фамилии соответствующих студентов
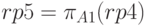
Получаем требуемый результат. Заметим, что для экономии действий и памяти, перед тем как склеивать таблицы, целесообразно было сделать операцию проекции отношения r1 на столбцы A1, A2. (чтобы не включать в декартово произведение лишние столбцы).
Введенные пять основных операций реляционной алгебры позволяют реализовать любой запрос к реляционной базе данных. Однако наряду с основными операциями достаточно часто удобно использовать так называемые дополнительные операции реляционной алгебры (которые могут быть выражены через основные).
Пересечением отношений r и s называется множество кортежей, принадлежащих как r, так и s. Пересечение может быть выражено через операции разности
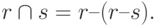
 -соединение
-соединение
 -соединение r и s по столбцам Ai и Aj представляет собой множество таких кортежей в декартовом произведении r и s, что i -й компонент r находится в отношении
-соединение r и s по столбцам Ai и Aj представляет собой множество таких кортежей в декартовом произведении r и s, что i -й компонент r находится в отношении  c j -м компонентом s, где
c j -м компонентом s, где  – арифметический оператор сравнения. Если
– арифметический оператор сравнения. Если  является оператором равенства, то эта операция называется эквисоединением
является оператором равенства, то эта операция называется эквисоединением
где l – арность отношения r.
Пример.
Заметим, что в примере 3 две последовательно идущие операции ( декартово произведение и селекция ) вместе как раз представляют операцию соединения. Причем использование декартова произведения для соединения таблиц обязательно обусловливает использование селекции как следующей операции для установления связи между таблицами. Поэтому целесообразно использовать такую объединенную операцию и программно реализовывать в СУБД именно операцию соединения.
Операция применима тогда и только тогда, когда столбцы имеют имена (являются атрибутами). Операция применима к отношениям, у которых есть одинаковые атрибуты.
Пусть
r = (A1, ..., Ak, B1,..., Bn), s = (A1, ..., Ak, C1,..., Cm),
имена A1, ..., Ak совпадают.
Тогда определяется следующим образом
определяется следующим образом
Для подчеркивания важности приведенных операций реляционной алгебры, а также для уточнения понятия реляционной СУБД приведем следующее определение одного из ведущих специалистов в области реляционных баз данных К.Дж. Дейта: " Будем называть систему реляционной, если она поддерживает, по крайней мере, реляционные базы данных, т.е. базы данных, которые могут восприниматься пользователем как таблицы и только как таблицы, операции селекции, проекции и соединения реляционной алгебры, не требуя при этом, чтобы каким-то образом были предопределены физические пути доступа для поддержки этих операций ".
Краткие итоги: В лекции рассматриваются вопросы, связанные с формализацией наиболее распространенной в настоящее время модели данных СУБД – реляционной модели. Формальное описание реляционной модели и полученные на этой основе математические методы и алгоритмы позволяют формализовать ряд шагов проектирования реляционной базы данных , получить оптимальную (по определенным критериям) структуру базы данных и эффективные алгоритмы обработки. Здесь рассматривается формализованное описание отношений, формальные средства манипулирования данными в реляционной модели (дано понятие реляционного исчисления и реляционной алгебры, приводятся основные операции реляционной алгебры ). Приводятся примеры представления запросов как последовательность формальных операций реляционной алгебры.
Вопросы, рассматриваемые в данной лекции, более подробно описаны в [ [ 2.1 ] - [ 5.7 ] ].