Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Уральский государственный экономический университет
Опубликован: 27.05.2014 | Доступ: свободный | Студентов: 467 / 49 | Длительность: 11:44:00
Темы: Математика, Экономика, Образование
Лекция 5:

Имитационное моделирование
A
|
версия для печати
< Лекция 4 || Лекция 5: 123 || Лекция 6 >

Статистические показатели

1000 реализаций:

R:=G(1000)

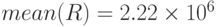mean(R)=2.22\times 10^6 - среднее

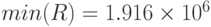min(R)=1.916\times 10^6 - минимальное

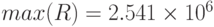max(R)=2.541\times 10^6 - максимальное

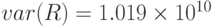var(R)=1.019\times 10^{10} - дисперсия

stdev(R)=1.01\times 10^5 - среднеквадратичное отклонение

Covar(R)=\frac{stdev(R)}{mean(R)} - коэффициент ковариации

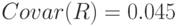
Covar(R)=0.045

10000 реализаций:

R1:=G(10000)

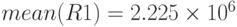mean(R1)=2.225\times 10^6 - среднее

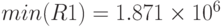min(R1)=1.871\times 10^6 - минимальное

max(R1)=2.754\times 10^6 - максимальное

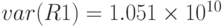var(R1)=1.051\times 10^{10} - дисперсия

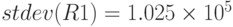stdev(R1)=1.025\times 10^5 - среднеквадратичное отклонение

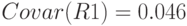Covar(R1)=0.046 - коэффициент ковариации

Гистограмма распределения для 10000 реализаций

Рис. 5.1. Гистограмма распределения для 10000 реализаций

j:=500

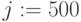
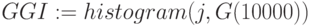
GGI:=histogram(j,G(10000))

GGI:=\begin{array}{|c|c|} \hline & 1 \\ \hline 1 & 1.87\cdot10^6 \\ \hline 2 & 1.871\cdot10^6 \\ \hline 3 & 1.873\cdot10^6 \\ \hline 4 & 1.874\cdot10^6 \\ \hline 5 & 1.875\cdot10^6 \\ \hline 6 & 1.877\cdot10^6 \\ \hline 7 & 1.878\cdot10^6 \\ \hline 8 & 1.88\cdot10^6 \\ \hline 9 & 1.881\cdot10^6 \\ \hline 10 & 1.883\cdot10^6 \\ \hline 11 & 1.884\cdot10^6 \\ \hline 12 & 1.885\cdot10^6 \\ \hline 13 & 1.887\cdot10^6 \\ \hline 14 & 1.888\cdot10^6 \\ \hline 15 & ... \end{array}

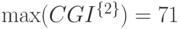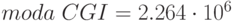
\max(CGI^{\{2\}})=71, moda\; CGI=2.264\cdot10^6

R:=G(10000)

RS:=mean(R), RD:=stdev(R)

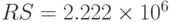RS=2.222\times 10^6, RD=1.014\times 10^5

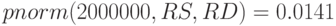
pnorm(2000000,RS,RD)=0.0141

Вероятность прибыли быть меньше 2000000 составляет 1,3%

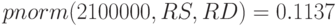
pnorm(2100000,RS,RD)=0.1137

Вероятность прибыли быть меньше 2100000 составляет 11%

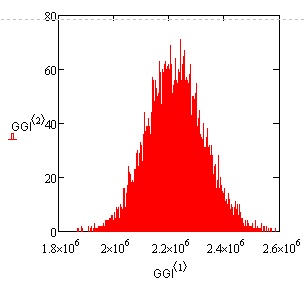
5.4. Результаты исследования прибыли

Вся информация результатов исследования прибыли для сценария распределения входных стохастических переменных показана в предыдущем разделе, где представлены решение задачи и результаты моделирования для входных данных из таблицы 5.1 и двух случайных совокупностей: 10000 и 5000 реализаций. Как видно, 1000 и 10000 реализаций дают очень близкие результаты по числовым характеристикам. Как правило, требуется знать наилучший и наихудший сценарии возможных событий. Статистические показатели для ожидаемой прибыли: минимальное значение - наихудшее (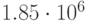1.85\cdot 10^6 руб.), максимальное значение - наилучшее (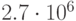2.7 \cdot 10^6 руб) , среднее – ожидаемое значение (2.22\cdot 10^6 руб) , представленные для двух случайных выборки, включающих 1000 и 10000 реализации модели практически не отличаются. Разброс значений относительно среднего (коэффициент вариации) составляет 5%. Риск получить прибыль, отличную от суммы 2447629 тыс.руб. равен 3%. Средняя прибыль \pm5\% включает значения от 2321055 до 2574204 (руб.). Вероятность попадания прибыли в этот интервал около 68%. С риском в 68% прибыль будет находиться в пределах от 2321055 руб. до 2574204 руб. Вероятность прибыли быть меньше 2,3 млн. около 12%. Это и составляет риск получения прибыли меньше 2,3 млн.

Показатели Среднее значение Среднеквадратичное отклонение Максимальное значение минимальное значение коэффициент вариации
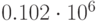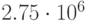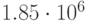Прибыль фирмы (руб) 2.22\cdot 10^6 0.102\cdot 10^6 2.75\cdot 10^6 1.85\cdot 10^6 4,6\%

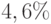Основные итоги

В лекции рассмотрены основные этапы имитационного моделирования. Изложен метод Монте Карло. Техника имитационного моделирования методом Монте-Карло представлена на примере исследования прибыли фирмы. Исследована оценка вероятности для предполагаемой прибыли принять значение меньше заданного. Построена имитационная модель в Mathcad. Задача решена с использованием специальных функций Mathcad для работы со случайными величинами. Все данные представлены в матричном виде. Применены методы программирования. Результаты представлены в виде статистических показателей и функций распределения.

Ключевые термины

Имитационное моделирование - техника численных экспериментов, с помощью которых можно получить эмпирические оценки степени влияния различных факторов - исходных величин, которые точно не определены, на зависящие от них результаты - показатели.

Имитационная модель - специальный программный комплекс, который позволяет имитировать деятельность какого-либо сложного объекта.

Стохастические переменные - переменные, значения которых не могут быть точно установлены или предсказаны.

Метод Монте-Карло - группа методов решения задач, в которых реализуется построение вероятностных распределений возможных значений выходной стохастической переменной при изменении входных переменных, которые генерируются в виде случайных последовательностей с заданными вероятностными характеристиками.

Компьютерная имитация - математическая модель, оперирующая сложной системой динамических уравнений и реализованная на ЭВМ.

Имитационный эксперимент – проведение серии имитационных расчетов в системном масштабе времени и по разработанному алгоритму.

Компьютерный эксперимент - эксперимент над математической моделью объекта исследования на ЭВМ, который состоит в том что, по одним параметрам модели вычисляются другие ее параметры и на этой основе делаются выводы о свойствах объекта, описываемого математической моделью.

Вероятностное распределение - закон, описывающий область значений случайной величины и соответствующих им вероятностей.

Статистические показатели – количественные характеристики вероятностного распределения случайной величины.

Дальше >>
< Лекция 4 || Лекция 5: 123 || Лекция 6 >

Вопросы и ответы

вопросов: 0