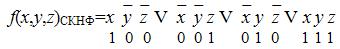Способы представления ФАЛ. Переход от одной формы представления ФАЛ к другой
Пример 2.3
Пусть ФАЛ задана сокращенной записью СКНФ:

Получить полную и сокращенную записи СДНФ этой функции.
Решение
Так как получение ТИ в данном примере не требуется, то можно использовать следующий подход.
Этап 1.
Получить сокращенную запись СДНФ этой функции. Для этого под знаком обобщенной дизъюнкции ? перечислить все наборы, не входящие в сокращенную запись СКНФ:

Этап 2.
Получить полную запись СДНФ согласно указаниям примера 2.1. Результатом будет:

Пример 2.4
Пусть ФАЛ задана в виде СДНФ:

Получить полную и сокращенную записи СКНФ этой функции.
Решение
Получим сокращенную запись СДНФ функции, для чего сначала определим двоичные эквиваленты наборов, соответствующих каждому конъюнктивному члену в полной записи СДНФ этой функции, поставив 1 под переменными, входящими в запись в прямом виде, и 0 под переменными, представленными в инверсном виде:
Затем представим эти наборы в десятичном коде и перечислим их под знаком обобщенной дизъюнкции ?:

По полученной сокращенной записи СДНФ функции получим сокращенную запись СКНФ, перечислив под знаком обобщенной конъюнкции ? номера наборов, не вошедших в сокращенную запись СДНФ:

По сокращенной записи СКНФ получим ее полную запись согласно методике, изложенной в примере 2.1.
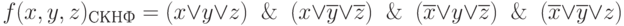
Пример 2.5
Пусть ФАЛ задана в виде СКНФ:

Получить полную и сокращенную записи СДНФ этой функции.
Решение
Получим сокращенную запись СКНФ этой функции. Для этого сначала определим двоичные эквиваленты наборов, соответствующих каждому дизъюнктивному члену в полной записи СДНФ этой функции, поставив 0 под переменными, входящими в запись в прямом виде, и 1 под переменными, представленными в инверсном виде:
Затем представим эти наборы в десятичном коде и перечислим их под знаком обобщенной конъюнкции ?:

По полученной сокращенной записи СКНФ функции получим сокращенную запись СДНФ, перечислив под знаком обобщенной дизъюнкции ? номера наборов, не вошедших в сокращенную запись СКНФ:
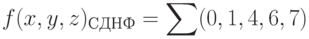
По сокращенной записи СДНФ получим ее полную запись согласно методике, изложенной в примере 2.1:
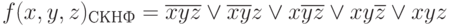
Пример 2.6
Пусть ФАЛ задана в виде дизъюнктивной нормальной формы, не являющейся совершенной. Например:

Получить полную и сокращенную записи СКНФ этой функции.
Решение
Для решения этой задачи можно сначала получить СДНФ функции.
Для получения СДНФ необходимо обеспечить зависимость каждого конъюнктивного терма от всех переменных, от которых зависит функция. Необходимые преобразования базируются на следующей эквивалентности:
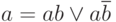
Тогда, последовательно повышая ранг для термов, зависящих не от всех переменных, получим:
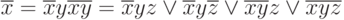
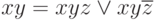

После выполнения преобразования на основе эквивалентности

получим полную, а затем и сокращенную записи СДНФ:
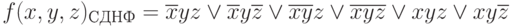
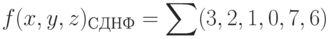
Последующие шаги по решению поставленной задачи рассмотрены ранее.
В результате получим:
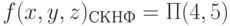
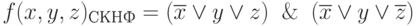
Пример 2.7
Пусть ФАЛ задана в виде конъюнктивной нормальной формы, не являющейся совершенной. Например:

Получить полную и сокращенную записи СДНФ этой функции.
Решение
Решение этой задачи аналогично предыдущей.
Для получения СКНФ необходимо использовать следующие эквивалентности:
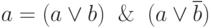

Тогда получим:
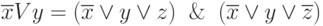

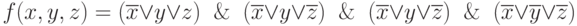
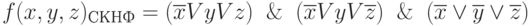

Исходя из полученной СКНФ функции, определим ее СДНФ:

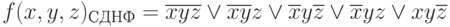
Пример 2.8


Представить запись этой функции в базисе "Штрих Шеффера".
Решение
Для перехода от представления ФАЛ в виде СДНФ к базису "Штрих Шеффера" необходимо выполнить следующее.
Этап 1.
Заменить все знаки дизъюнкции и конъюнкции на знак функции "Штрих Шеффера". При этом вследствие невыполнения для данной функции ассоциативного закона (см. (1.32)) каждый конъюнктивный член должен быть заключен в скобки:
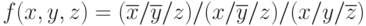
Этап 2.
Выразить функцию отрицания через функцию "Штрих Шеффера" согласно (1.29), также заключая эту операцию в скобки:
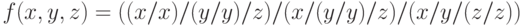
Пример 2.9
Пусть ФАЛ задана в виде:
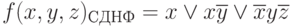
Представить запись этой функции в базисе "Штрих Шеффера".
Решение
Особенность выполнения первого этапа обусловлена наличием в записи функции члена x, не являющегося конъюнкцией каких-либо переменных. Для приведения этой функции к дизъюнктивной нормальной форме воспользуемся выражением (1.10):

Дальнейшие действия в этом примере полностью совпадают с примером 2.8.
Результатом выполнения этапа 1 будет

а окончательный результат:
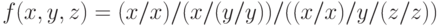
Краткие итоги
В лекции рассматриваются различные формы представления логических функций. Если представление ФАЛ в виде таблицы истинности используется, как правило, на начальном этапе проектирования с целью дать возможность разработчику как можно более точно сформулировать свои требования к проектируемому узлу вычислительной техники, то представление логической функции в аналитическом виде в совершенной дизъюнктивной или конъюнктивной нормальной форме позволяет в дальнейшем провести минимизацию этой функции. В лекции показаны многочисленные примеры перехода от одной формы представления функции к другой, а также методы получения совершенных нормальных форм в том случае, если аналитическая запись ФАЛ не является совершенной формой.
Контрольные вопросы и упражнения
- Назовите формы представления логических функций.
- Каким образом составляется таблица истинности ФАЛ?
- Для каких целей используется представление логической функции в виде таблицы истинности?
- Для каких целей используются совершенные формы представления логических функций?
- Как можно получить совершенную дизъюнктивную нормальную форму, используя таблицу истинности этой ФАЛ?
- Представьте СДНФ функции "суммы по модулю 2".
- Как можно получить совершенную конъюнктивную нормальную форму, используя таблицу истинности этой ФАЛ?
- Как можно получить совершенную конъюнктивную нормальную форму, используя таблицу истинности ФАЛ на основе ее совершенной дизъюнктивной нормальной формы?
- Получите СДНФ ФАЛ, СКНФ которой выглядит следующим образом: f(a,b,c,d) = ?(2, 4, 6, 7, 8, 10 , 11, 14).
- Составьте таблицу истинности логической функции, совершенная дизъюнктивная форма которой имеет вид: f(x, y, z) = ?(1, 2, 6, 7).