Игра "Быки и коровы"

Как растут функции или эффективные алгоритмы

Наигравшись, стоит немного заняться математикой, связанной с этой задачей. Давайте рассмотрим три функции:

F1(n) = Log(n); F2(n) = n; F3(n) = 2ⁿ

Эти функции соответственно называются: логарифмической, линейной, экспоненциальной. Они часто появляются в самых разных задачах, связанных с программированием. Хорошо бы понимать, как ведут себя эти функции, как они растут при изменении аргумента n. Когда n мало, то значения функций не сильно отличаются. Например, при n, равном три, все значения находятся в пределах десяти. При n, равном десяти, разность между линейной и логарифмической функцией все еще находится в пределах десятка, но экспоненциальная функция превосходит линейную функцию уже в сто раз. С ростом n экспонента взмывает как ракета и уходит в небеса. При n, равном 100, 2¹⁰⁰– это невообразимо большое число, превосходящее число атомов в нашей вселенной. Но также как экспонента превосходит линейную функцию, так линейная функция превосходит логарифмическую. Например, при n, равном одному миллиону, значение логарифмической функции близко к двадцати.

Какое отношение это имеет к алгоритмам? Самое прямое. Если число операций задается логарифмической функцией, то человек может справиться с задачей даже при больших значениях n, например, равных миллиону. Если число операций определяется линейной функцией, то человек уже не в состоянии выполнить такое количество операций, но компьютер легко справится с такой задачей. Когда же число операций задается экспоненциальной функцией, то эта задача не по силам компьютеру уже при значениях n, больших 30 – 40.

Вернемся к нашей задаче поиска задуманного числа. Существует ли более простой алгоритм, чем тот, который был реализован при поиске задуманного числа компьютером. Конечно, есть простой переборный алгоритм. Перебираем число за числом в заданном интервале, пока не наткнемся на задуманное число. Число операций в таком алгоритме определяется линейной функцией. Как нам понятно, переборный алгоритм в нашей игре можно применять, только тогда, когда задуманное число находится в малом интервале, содержащем не более одного, двух десятков чисел. Когда в интервале чисел миллион, человек не может найти задуманное число, применяя переборный алгоритм. Ему может помочь только алгоритм бинарного поиска, число операций в котором определяется логарифмической функцией.

А встречаются ли в программировании задачи, например, игры, в которых число операций задается экспонентой? В математике существует много легенд, связанных с экспонентой, ее взрывным ростом, не заметным при малых значениях. Давайте познакомимся с игрой "Ханойские башни". Вот цветистое описание этой игры:

В величественном храме Бенареса под куполом, отмечающим центр мира, на медной плите установлены три бриллиантовых стержня. Каждый стержень, высотой в локоть, и тонок, как пчелиная талия. На один из этих стержней в начале мироздания Бог поместил 64 диска из чистого золота. Самый большой диск покоится на медной плите, а остальные, друг друга меньше, создают пирамиду, подымающуюся к вершине стержня. Это и есть священная башня Брахмы.

Ночью и днем неустанно священники, сменяя друг друга, работают, чтобы перенести священную башню на третий бриллиантовый стержень, не нарушив при этом священных правил, установленных Брахмой. Когда их работа будет закончена, падет башня, падут брахманы и наступит конец мира.

Правило Брахмы требует, чтобы при переносе колец на всех стержнях присутствовала пирамида. Это означает, что нельзя положить диск поверх диска меньшего размера. Нетрудно решить эту задачу, когда число дисков равно трем, - понадобится всего семь перекладываний. Когда в детстве я играл в эту игру, то дисков было 6 или 7. За несколько минут я мог решить поставленную задачу. А как обстоит дело с брахманами, которые работают уже несколько сотен лет. Скоро ли они закончат свою работу и наступит конец мира? Можно не беспокоиться. Их работа не будет закончена в обозримом будущем, скорее погаснет наше солнце. Дело в том, что число перекладываний определяется экспонентой, оно равно 2ⁿ– 1. При n, равном 64, число перекладываний равно 2⁶⁴, что примерно равно . Это огромное число. Не только человек, но и ни один компьютер не может справиться с этой задачей.

Сегодня все развитые страны соревнуются в построении суперкомпьютера, работающего с экзафлопной производительностью, то есть способного выполнять 10¹⁸операций в секунду. Но и такой суперкомпьютер не справится с нашей задачей. Дело в том, что суперкомпьютеры обладают столь высокой производительностью за счет того, что у них миллионы параллельно работающих ядер. Но задача "Ханойские башни" не допускает параллельного решения. Золотые диски нужно перекладывать последовательно. Поэтому только одно ядро суперкомпьютера будет участвовать в решении задач и жизни многих поколений не хватит компьютеру, чтобы справиться с задачей.

Какой вывод следует из наших рассмотрений? Когда мы строим наши алгоритмы, то иногда приходится думать о построении эффективных алгоритмов. Алгоритм бинарного поиска эффективнее алгоритма полного перебора.

На этом разбор этого проекта закончим и перейдем к рассмотрению следующей игры на эту же тему.

Игра "Быки и коровы"

В этой игре также, как и в предыдущей, компьютер загадывает число из некоторого интервала, а игрок должен отгадать заданное число за K вопросов, чтобы получить звание "Магистр игры". Игра более сложная, поскольку компьютеру можно задавать вопрос только одного типа: "Задуманное число равно N?". Число N имеет столько же цифр, как и задуманное число. В ответ на вопрос компьютер сообщает сколько в предъявленном числе N быков и сколько коров. Быком называется цифра числа N, совпадающая по значению и по месту с цифрой задуманного числа. Корова – это цифра, совпадающая по значению, но не совпадающая по месту. Рассмотрим пару чисел, в которой первым является задуманное число, а вторым числом пары является предъявляемой число N. Для пары чисел (1254, 5237) ответом будет "один бык, одна корова". Число отгадано, когда все цифры предъявленного числа являются быками.

В определении коровы есть момент, допускающий неоднозначное толкование. Рассмотрим следующую пару чисел (1254, 2222). В этой ситуации возможны два ответа: "один бык и три коровы" и "один бык и ноль коров". В нашем алгоритме правильным считается второй ответ. Если некоторая цифра отождествлена с быком, то она не участвует в поисках коров.

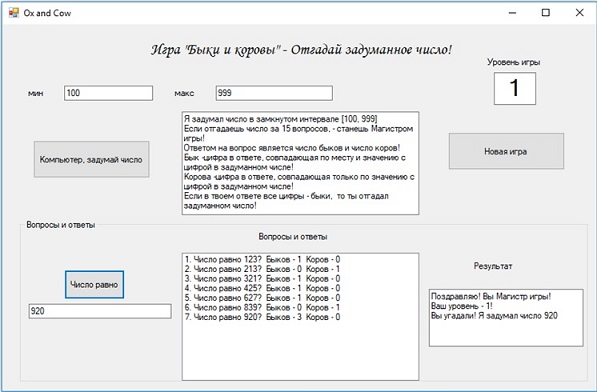
Рассмотрим интерфейс игры:

увеличить изображение
Рис. 5.1. Интерфейс игры "Быки и коровы" на этапе завершения игры

Можно видеть, что во-многом интерфейс схож с интерфейсом предыдущей игры. Давайте рассмотрим логику рассуждений, приведшую к разгадке задуманного числа. Поскольку вначале никакой информации нет, то предлагается любое число из трех цифр, в данном случае 123. Из ответа ясно, что одна из этих цифр присутствует в задуманном числе, причем стоит на своем месте. Перестановка цифр дает дополнительную информацию. Из ответа на второй вопрос ясно, что цифры 3 в задуманном числе нет, поэтому кандидатом является либо цифра 1, либо 2. Из ответа на третий вопрос становится ясно, что быком является цифра 2. Поэтому далее испытываются оставшиеся цифры. Из ответов на 4-й и 5-й вопросы следует, что в задуманном числе нет цифр 4, 5, 6, 7. Из ответа на 6-й вопрос следует, что в задуманном числе могут быть цифры 0, 8, 9, стоящие на первом и третьем месте. Проба 920 оказалась решающей, поиск завершился успехом.

Способ рассуждений понятен человеку, и он может успешно решать поставленную задачу, создавая разумную комбинацию, зависящую от ответов компьютера. Так что человек разумный вполне может стать Магистром игры. А можно ли написать программу для компьютера столь же эффективную, как и для предыдущей игры, где компьютер не проигрывает человеку. Ответ не очевиден.

Давайте рассмотрим, как устроен код нашей игры. Начнем с рассмотрения переменных.

Переменные и константы игры

Искусство программирования состоит в том, чтобы придумать, спроектировать алгоритм, решающий задачу. Не менее важной, дополняющей стороной этого процесса является умение спроектировать необходимую структуру данных, с которой и работает алгоритм. Как видите, для нашей, не простой, но и не слишком сложной задачи требуется определить более десятка переменных и большое количество констант, поддерживающих вывод разумных ответов, понятных пользователю.

Поскольку данная игра во многом совпадает с предыдущей, то и можно отметить существенное пересечение списков констант и переменных в обеих играх. Вот список переменных и констант, используемых в данной игре:

//переменные, необходимые для организации игры
        int level_game;             //уровень игры
        Random rnd = new Random();  //генератор случайных чисел
        int digits;             //число цифр в задуманном числе
        int min;                //минимальное значение задуманного числа
        int max;                //максимальное значение задуманного числа
        int number;             //задуманное число
        int N;                  //число вопросов для звания Магистр
        int answer;             //текущий ответ
        int ox_n;               //число быков  в текущем ответе
        int cow_n;              //число коров  в текущем ответе        
        int countQuestion = 0; //текущее число заданных вопросов
        string question;        //очередной вопрос

        //константы для организации диалога
        const string ANSW =
               "Я задумал число в замкнутом интервале [";
        const string ANSW1 =
            "Если отгадаешь число за ";
        const string ANSW2 =
            " вопросов, - станешь Магистром игры!\r\n";
        const string ANSW3 =
            "Ответом на вопрос является число быков и число коров!\r\n";
        const string ANSW31 =
            "Бык -цифра в ответе, совпадающая по месту и значению" +
            " с цифрой в задуманном числе!\r\n";
        const string ANSW32 =
            "Корова -цифра в ответе, совпадающая только по значению" +
            " с цифрой в задуманном числе!\r\n";
        const string ANSW33 =
            "Если в твоем ответе все цифры - быки, " +
            " то ты отгадал задуманном число!\r\n";
        const string ANSW4 =
            "Поздравляю! Вы Магистр игры!\r\n";
        const string ANSW44 = "Ваш уровень - ";
        const string ANSW5 = "Вы угадали! Я задумал число ";