Теория групп
Группы - математический инструментарий для изучения симметрий. Идея теории групп состоит в обобщении алгебры чисел, расширяя ее до алгебры симметрий. Группу можно ассоциировать с любым симметричным объектом, будь то объект материального мира или абстрактная математическая конструкция.
Неформально трансформация симметрии объекта, перемещая точки объекта, сохраняет его как целое. Хорошим примером, который всегда стоит иметь ввиду, говоря о группах, является вращение сферы. Когда мы вращаем сферу, то ее точки движутся, но сфера как множество точек сохраняется неизмеиной. Группу можно рассматривать как множество всех трансформаций симметрии данного объекта.
Концепция симметрии сыграла центральную роль в разработке физики 20-го века. Хотя использование симметрии в физике восходит к Галилею, Эйнштейн был тем, кто сделал симметрию краеугольным камнем физики. Ему удалось построить теорию относительности, исходя из единственного постулата о геометрия такого объекта как " пространство - время" и трансформаций симметрия этого объекта.
Вот несколько общих принципов, универсально справедливых для трансформаций симметрии любого объекта:
- Каждая трансформация симметрия обратима. Например, если мы повернули сферу на угол
 вокруг какой-либо оси, то, чтобы обратить эту трансформацию, достаточно повернуть сферу на тот же угол вокруг той же оси в противоположном направлении.
вокруг какой-либо оси, то, чтобы обратить эту трансформацию, достаточно повернуть сферу на тот же угол вокруг той же оси в противоположном направлении. - Композиция двух трансформаций симметрии является трансформацией симметрии. Мы можем повернуть сферу вокруг некоторой оси на угол
 , а затем повернуть сферу относительно другой оси на угол
, а затем повернуть сферу относительно другой оси на угол  . Понятно, что композиция этих трансформаций сохраняет сферу Менее очевидно то, что эти два поворота можно заменить одним поворотом на некоторый угол вокруг третьей оси.
. Понятно, что композиция этих трансформаций сохраняет сферу Менее очевидно то, что эти два поворота можно заменить одним поворотом на некоторый угол вокруг третьей оси. - Всегда существует тривиальная трансформация симметрии, которая ничего не делает, не перемещая ни одной точки. Такую трансформацию будем называть трансформацией тождественности.
Сохраняя в памяти эти принципы, мы можем теперь дать формальное определение группы.
Определение. Группа G - это множество элементов с:
- выделенным элементом е, называемым единичным или тождественным элементом;
- операцией обращения (инверсии) элементов
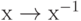 ;
; - операцией умножения пары элементов
 .
.
Для всех элементов х, у, z из G имеет место:
- х * е = е * х = х; (аксиома тождественности)
-
 ; (аксиома инверсии)
; (аксиома инверсии) - (х * у) * z = х * (у * z); (закон ассоциативности).
Мы можем непосредственно видеть, что аксиомы тождественности и инверсия выполняются для всех трансформаций симметрии. Оказывается, что закон ассоциативности является универсальным и выполняется для композиции трансформаций (аргументация, которую мы использовали для доказательства справедливости ассоциативного закона в случае линейных трансформаций, применима и в более общем контексте).
Еще раз укажем на контринтуитивный характер операции композиции 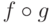 . Когда композиция применяется к некоторому аргументу р, то первой выполняется трансформация g, а затем к результату применяется трансформация f :
. Когда композиция применяется к некоторому аргументу р, то первой выполняется трансформация g, а затем к результату применяется трансформация f : 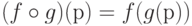
Первые примеры групп приходят из арифметики.
Рассмотрим множество 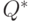 - ненулевых рациональных чисел. Это множество замкнуто относительно операций умножения и обращения рациональных чисел. Единичным (тождественным) элементом является число 1. На множестве выполняются все три аксиомы, так что, по определению,
- ненулевых рациональных чисел. Это множество замкнуто относительно операций умножения и обращения рациональных чисел. Единичным (тождественным) элементом является число 1. На множестве выполняются все три аксиомы, так что, по определению, 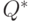 -это группа.
-это группа.
Еще одним примером числового множества, представляющего группу, является множество 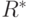 - множество ненулевых вещественных чисел. (Заметьте, чтобы получить мультипликативную группу из множества вещественных чисел и множества рациональных чисел удаляется 0, так как для этот элемента первые две аксиомы не выполняются.)
- множество ненулевых вещественных чисел. (Заметьте, чтобы получить мультипликативную группу из множества вещественных чисел и множества рациональных чисел удаляется 0, так как для этот элемента первые две аксиомы не выполняются.)
Мы можем рассмотреть группы с операцией, отличной от умножения. На самом деле важно не имя операции, а ее свойства. Давайте дадим другое определение группы, назвав операцию, применяемую к паре элементов множества, сложением. С операцией сложения аксиома тождественности имеет вид: х + е = е + х = х. Ясно, что при операции сложения в арифметике роль тождественного элемента играет 0. Поэтому для аддитивных групп (групп с операцией сложения) тождественный элемент обозначается как "0". Аксиома инверсии в этом случае говорит, что сумма элемента с его обратным элементом равна 0. Понятно, что обратный элемент к элементу х рассматривается в этом случае как отрицательный элемент и обозначается как -х.
Это дает нам множество примеров аддитивных групп:
- Множество целых чисел с операцией сложения (Z, +);
- Множество рациональных чисел с операцией сложения (Q, +);
- Множество вещественных чисел с операцией сложения (R, +);
- Любое векторное пространство с операцией сложения (V, +).
B примерах, приходящих из арифметики, для элементов часто выполняется и коммутативный закон: х у = у * х (х + у = у + х для аддитивных групп). Коммутативный закон не является частью законов группы. Для многих групп этот закон не выполняется. Группы, удовлетворяющие коммутативному закону, называются коммутативными или абелевыми группами (в честь норвежского математика Нильса Абеля).
Примером некоммутативной группы является множество обратимых квадратных матриц размера N * N. Эта группа называется обобщенной линейной группой (General Linear group) и обозначается как GL(N). Единичным элементом этой группы является единичная матрица I. Множество замкнуто относительно операции умножения матриц, так как существует формула для обращения произведения матриц: