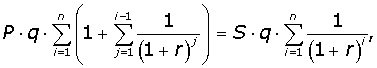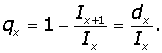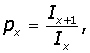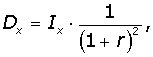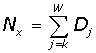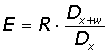Понятие страховой деятельности и ее организации

16.3.1. Финансовые ренты в страховании

В страховании используются так называемые условные ренты (contingent annuity) - аннуитеты. В финансовых расчетах используется вероятностный подход наступления определенных событий денежного потока - поступлений или выплаты денег. В страховании выплата ренты зависит от наступления страхового события.

Согласно договору страхования страхователь выплачивает вперед страховщику страховую премию (premium) - P, которая дает право на получение страховой суммы - S после наступления страхового случая, вероятность которого - q.

Без учета фактора времени принцип эквивалентности обязательств страхователя и страховщика имеет вид:

P = S · q

Для учета фактора времени вводится ставка дисконтирования будущих сумм, которая приводит их к настоящему моменту времени. Например, для имущественного страхования выполняется соотношение:

Левая часть выражения содержит оценку выплат премии страхователя страховщику за n учетных периодов, если известна ставка дисконтирования - r, а также постоянное значение вероятности наступления страхового случая - q, размера премии - P. Правая часть выражения содержит оценку выплат страховщиком.

Как правило, в имущественном страховании суммы периодических выплат являются постоянной величиной, а в личном страховании - переменной, зависящей от возраста застрахованного.

Например, при разработке страховых потоков платежей используются значения вероятностей дожития до определенного возраста, смерти в определенном возрасте. Используются разработанные на основе статистических данных таблицы смертности. Применительно для 100 тыс. человек вычисляется количество людей, которые доживают до определенного возраста x - I_x, количество умерших в течение года после возраста x - d_x, вероятность умереть в течение года после возраста x - q_x:

I_{x + 1} = I_x - d_x, d_x = I_x · q_x.

Величина q_x вычисляется по формуле

Соответственно, p_x - вероятность прожить еще 1 год при условии достижения возраста x:

p_x + q_x = 1

Вероятность дожить от возраста x до возраста n:

В актуарных расчетах используются так называемые коммутационные числа (функции):

• число доживающих до определенного возраста людей;
• число умерших до определенного возраста людей.

Вводятся показатели, используемые для упрощения расчетов:

Например, страхование жизни (дожитие до определенного возраста). В договоре страхования оговариваются: исходный возраст - x, возраст дожития - w, сумма выплат - R, процентная ставка дисконтирования - r.

Сбалансированность взносов и выплат - обязательное условие для выполнения обязательств страховщика.

Премия, выплачиваемая страховщику: 

. Нетто-ставка страхования на дожитие равна отношению  она зависит от трех параметров: x, w, r (без учета инфляции). Для пенсионного страхования в условиях развития негосударственных пенсионных фондов (НГПФ) встает вопрос о страховых аннуитетах, тарифах и пенсиях. В рамках НГПФ применяются два основных метода обеспечения пенсиями:

• страховой - коллективное или индивидуальное страхование пенсий, при этом страховые суммы не предусматривают наследование остатков средств на счете участника в случае его смерти;
• сберегательный или трастовый, покупка финансовой ренты, накопленные суммы предполагают наследование суммы выплат.