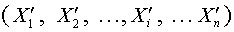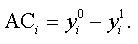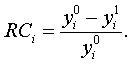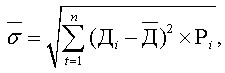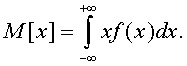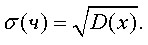|
Как получить сертификат, если нет экзамена? |
Методы и модели планирования стратегии предприятия
3.7. Формирование программы риск-менеджмента, методы анализа и регулирования риска в долгосрочном инвестировании
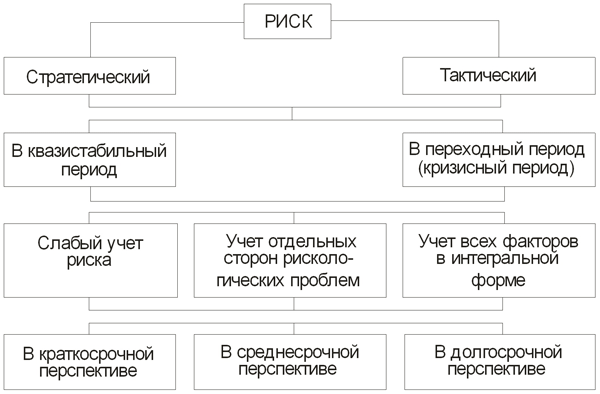
При создании системы управления рисками каждое предприятие должно исходить из того, что риски могут иметь стратегическую и тактическую основу (см. рис. 3.25).
Следует различать стратегические риски для квазистабильных и переходных (кризисных) периодов жизнедеятельности. Квазистабильные стратегические риски связаны с миссией организации, а переходные (кризисные) - с инновационной деятельностью. В зависимости от временных рамок планирования различают стратегическое и оперативное планирование. Чем больший срок охватывает планирование, тем менее надежны исходные данные.
Риск в стратегическом планировании - это вероятность возникновения убытков или снижения доходов по сравнению с прогнозируемым вариантом. Выбранная стратегия часто связана с реализацией идей новвоведений, внедрением крупных и многофакторных мероприятий, которые можно назвать проектами. Реализация таких проектов всегда связана с большими инвестициями и определенным риском. Это характерно как для стратегии с наступательным планом, так и с оборонительным. Инвестиционный проект может оказаться нереализованным, неэффективным или менее эффективным, чем намечалось. Причины неудач могут носить внешний или внутренний характер.
Риск может рассматриваться как вероятность ошибки при выборе стратегических альтернатив. Он может появиться при неправильном управленческом решении по выбору инвестиционного проекта или определении путей его реализации. Выход на рынок с новым товаром всегда сопровождается повышенным риском из-за отсутствия, например, спроса на незнакомую продукцию. Это риск невостребованности продукции, ущерб от него возрастает по мере продвижения продукции по этапам производственного цикла.
Традиционный риск-менеджмент представляет собой систему управления риском и экономическими (прежде всего финансовыми) отношениями, возникающими в процессе управленческих действий. Алгоритм управления рисками предприятия можно представить следующим образом (см. рис. 3.26).
Для эффективного управления рисками на первом этапе предстоит определить место механизма этого управления в общей стратегии предприятия (см. рис. 3.26).
При проведении первичного анализа рисков определяются наиболее значимые из них, оцениваются рискообразующие факторы. Имеет место некоторая приемлемость риска, поэтому при формировании стратегии предварительно проводится качественный анализ. Он позволяет выявить зоны риска для данной стратегии и определить вероятность наступления риска. Формируется перечень рисков и выявляются причины возникновения проблемной ситуации. Возможные риски ранжируются, выделяются наиболее вероятные и важные, что позволяет на основе анализа прогнозировать их появление в планируемом периоде.
С учетом субъективной оценки риска формируются основные направления его минимизации (см. рис. 3.26). Если возможно принять различные варианты решения, выбирается такой, при котором вероятность риска наименьшая. Если же различные варианты в итоге дают один и тот же результат, выбирается решение, основанное на более качественной информации. При этом нельзя упустить ее стоимость.
Проводится детальный и преимущественно количественный анализ риска (см. рис. 3.26), связанный с оценкой степени риска как отдельных направлений, так и проекта в целом. Степень риска - это вероятность наступления случая потерь, а также размер возможного ущерба от него. Вероятность каждого типа рисков и убытки, вызываемые ими, различны, поэтому их следует спрогнозировать и, по возможности, рассчитать. Способы расчета разнообразны и достаточно широко освещены в экономической литературе. Для крупных проектов необходим тщательный просчет рисков с использованием специального, иногда сложного математического аппарата теории вероятности, для относительно небольших бывает достаточно проанализировать риск с помощью экспертных методов. Конкретно о методах анализа риска будет сказано далее. При проведении детального анализа по наиболее значимым рискам целесообразно провести оценку возможных потерь: материальных, трудовых, финансовых, специальных. Завершая анализ, можно определить тип области риска деятельности предприятия (безрисковая, повышенного риска, критического риска, недопустимого).
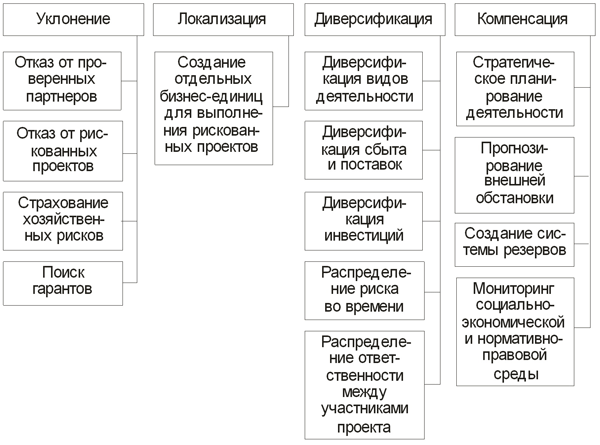
При разработке мероприятий по минимизации рисков (см. рис. 3.26) оценивается эффективность мероприятий, фактическая возможность их реализации, проводится юридическая экспертиза. Управленческие решения по минимизации риска зависят от времени обнаружения и объема ущерба. Особое внимание следует уделить методам компенсации и снижения риска, т.е. предотвращению неблагоприятных событий или ослаблению их негативного эффекта. Для снижения степени риска применяются различные приемы (см. рис. 3.27).
Если в качестве меры снижения рисков предусмотрено уклонение, например страхование, предлагается составить программу страхования рисков. Страхование риска - это передача определенных рисков страховой компании (имущественное страхование и страхование от несчастных случаев). Наиболее распространенный метод снижения риска - не вкладывать средства в сомнительные проекты.
Распределение риска реализуется в процессе подготовки проекта и контрактных документов. В процессе переговоров с инвестором участники проекта должны проявлять максимальную гибкость относительно того, какую долю риска они согласны принять на себя. Для количественного распределения риска в проекте можно использовать модель, основанную на "дереве решений".
Создание системы резервов также является одним из способов борьбы с риском. Средства резервируются на покрытие непредвиденных расходов. Устанавливаются соотношения между потенциальными рисками, влияющими на стоимость проекта, и размером расходов, необходимых для преодоления сбоев в его выполнении. Серьезной проблемой является проведение оценки потенциальных последствий рисков, т.е. определение сумм на покрытие непредвиденных расходов. Для ее решения можно использовать все (указанные далее по тексту) методы анализа рисков. Определяется также структура резервов на покрытие непредвиденных расходов. В общий финансовый план на перспективу входит программа риск-менеджмента (см. рис. 3.26), в которой определяется комплексное влияние мероприятий по минимизации риска на финансовое состояние, вносятся затраты и результаты программы, оцениваются вероятные последствия неблагоприятных ситуаций, планируются меры снижения их воздействия.
Абсолютный объем финансовых потерь, связанных с реальным инвестированием, представляет собой сумму убытка (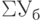 ), причиненного инвестору в связи с неблагоприятными обстоятельствами. Относительный размер финансовых потерь или коэффициент инвестиционного риска (kи.р) определяется в процентах:
), причиненного инвестору в связи с неблагоприятными обстоятельствами. Относительный размер финансовых потерь или коэффициент инвестиционного риска (kи.р) определяется в процентах:
Принято считать, что финансовые потери будут низкими, когда их уровень к объему инвестиций по проекту не превышает 5%; средними, когда это значение находится в пределах выше 5 и до 10%; высокими - более 10 и до 20%; очень высокими, когда значение превышает 20%.
Контроль в общей системе управления рисками (см. рис. 3.26) служит средством получения обратной связи. На основе его данных проверяется выполнение мероприятий по минимизации рисков и дается соответствующая оценка, по возможности устраняются выявленные причины отклонений от намеченного плана или корректируются данные программы риск-менеджмента. В плане желательно предусмотреть соответствующие решения, которые могут быть реализованы в случае наступления неблагоприятных событий. Это позволит своевременно внести в план коррективы, т.е. в какой-то мере разрешить возникшую проблему, оценить упущенную выгоду. Поиск правильного решения задач с информационной неопределенностью во многом зависит от способности менеджеров, которые принимают решения в процессе этапов планирования, на каждом из которых может возникнуть риск.
Понимания экономической природы инвестиционного риска недостаточно для эффективного управления долгосрочными вложениями. На первое место выходят способы и методы непосредственного воздействия на уровень риска с целью его максимального снижения. Методы анализа и регулирования риска в долгосрочном инвестировании разнообразны и достаточно широко освещены в экономической литературе.
Одна из современных методик детального расчета рисков разработана Инвестиционно-финансовой группой и Российской финансовой корпорацией. Методика предусматривает решение четырех задач:
- составление исчерпывающего перечня рисков с одновременным делением их на простые и сложные;
- определение удельного веса каждого простого риска по всей их совокупности. Поскольку сложные (составные) риски являются объединением простых, каждый из которых в свою очередь рассматривается как простой;
- проведение оценки вероятности наступления событий, относящихся к каждому простому риску;
- определение балльной оценки по всем рискам проекта.
В справочном пособии по управлению проектами предлагаются следующие методы определения риска:
- анализ чувствительности;
- проверка устойчивости и вычисление предельных значений параметров проекта;
- определение точки безубыточности;
- корректировка параметров проекта;
- построение "дерева решений";
- формализованное описание неопределенности.
Основные методы в определенной последовательности с учетом степени математической сложности составляющих методики были приведены в работе. Подобная классификация методов с некоторыми дополнениями по видам методов представлена в табл. 3.34. Деление методов по степени математической сложности оправдывается тем, что классификация методов оценки инвестиционного риска по каким-либо иным признакам является неоднозначной и сложной. Часто в литературе приводится перечень неклассифицируемых возможных методов. Укажем на основные методы, применяемые на практике и исследуемые в специальных изданиях. Оценим возможность и необходимость использования отдельных методов и моделей для анализа и регулирования риска в долгосрочном инвестировании.
| Группа методов | Вид методов |
|---|---|
| 1. Простые математические методы (первая группа) | 1.1. Корректировка параметров инвестиционного проекта (метод вариации параметров).
1.2. Корректировка на искажения в системе бухгалтерского учета. 1.3. Проверка устойчивости и определение предельных значений параметров проекта. 1.4. Метод использования аналогов |
| 2. Методы средней сложности (вторая группа) | 2.1. Метод экспертных оценок.
2.2. Построение "дерева решений". 2.3. Анализ чувствительности проекта. 2.4. Составление и анализ балансов предприятия с учетом будущего прироста активов и связанного с этим риска |
| 3. Сложные математические методы (третья группа) | 3.1. Формализованное описание неопределенности.
3.2. Дисперсионный и иной статистический анализ. 3.3. Имитационные модели (включая САРМ, ОРТ, метод Монте-Карло и др.). 3.4. Энтропия инвестиционного проекта |
К первой группе методов анализа и регулирования риска инвестиционных проектов отнесены те, чья математическая основа относительно проста (см. табл. 3.34).
Простым методом является корректировка параметров инвестиционного проекта на недооценку отрицательных факторов (на оптимизм). В целом эта корректировка сводится к завышению расходных и занижению доходных факторов проекта. Излишний оптимизм разработчиков проекта часто усиливается заинтересованностью предприятия в целом либо конкретных менеджеров в том, чтобы принять наиболее оптимальное решение об инвестировании. Сущность рассматриваемого метода заключается в намеренном ухудшении ряда инвестиционных аргументов (параметров) и уменьшении результирующего показателя инвестиционного проекта.
В таблице 3.35 приведен примерный перечень основных параметров, подлежащих корректировке, который часто приводится в работах, связанных с анализом инвестиционных проектов. В таблицах 3.36 и 3.37 даны примеры корректировок исходных данных инвестиционного проекта, которые носят условный характер, а диапазон корректировок для наглядности увеличен.
Для инвестиционного проекта рассчитаны корректировки по семи параметрам (см. табл. 3.36).
Значение параметров указано до и после корректировки в процентах от первоначального. Значение откорректированной инвестиционной функции приведено без влияния иных факторов. Итог откорректированной инвестиционной функции рассчитан исходя из параметров X'
, т.е. все значения аргументов подвергнуты исправлению.Дальнейшую обработку данных предложено производить с введением нескольких дополнительных характеристик, отражающих количественные параметры прошедшей корректировки.
Так, абсолютная корректировка для i-го параметра АСi равна разнице между yi0 и yi1:
| Наименование параметра | Диапазон |
|---|---|
| 1. Сроки регистрации, получения лицензии или разрешения. | плюс 1-12 мес. |
| 2. Сроки строительства и (или) поставки, монтажа оборудования. | плюс 1-12 мес. |
| 3. Производственные простои в силу технических причин. | минус 5-15% производственных мощностей |
| 4. Производственные простои в силу недостатков снабжения и сбыта. | минус 10-20% производственных мощностей |
| 5. Себестоимость по прямым затратам. | плюс 10-15% |
| 6. Накладные расходы. | плюс 15-25% |
| 7. Цены на готовую продукцию. | минус 5-15% |
| 8. Проценты по кредитам и займам. | плюс 20-30% |
| 9. Оборачиваемость дебиторской задолженности. | плюс 20-30% |
| 10. Оборачиваемость кредиторской задолженности | минус 20-30% |
| Наименование параметра | Значение параметра, % от первоначального | Значение инвестиционной функции | ||
|---|---|---|---|---|
| до | после | до | после | |
| 1. Сроки регистрации. | 100 | 200 | 7 731 800 | 7 566 920 |
| 2. Сроки строительства. | 100 | 150 | 7 731 800 | 7 608 140 |
| 3. Производственные простои в силу технических причин. | 100 | 115 | 7 731 800 | 7 718 120 |
| 4. Производственные простои в силу недостатков сбыта. | 100 | 120 | 7 731 800 | 7 549 400 |
| 5. Себестоимость по прямым затратам. | 100 | 110 | 7 731 800 | 6 818 660 |
| 6. Накладные расходы. | 100 | 120 | 7 731 800 | 7 674 800 |
| 7. Цена на готовую продукцию | 100 | 90 | 7 731 800 | 6 006 980 |
| Итого | 7 731 800 | 4 720 110 | ||
Эта корректировка показывает, насколько изменилось значение инвестиционной функции в результате перехода i-го параметра.
Для перехода к безразмерным величинам вводится относительная корректировка для i-го параметра RCi, равная разнице между yi0 и yi1, выраженной в величинах yi0:
Величина RCi характеризует относительное изменение инвестиционной функции - сдвиг нового значения параметра в долях величины неоткорректированного (см. табл. 3.37).
По полученным результатам можно судить о том, что особое внимание следует уделить тем параметрам, относительная корректировка которых минимальна (максимальна по модулю). Итоговые формы корректировок желательно сортировать по возрастанию параметра RCi (см. табл. 3.37). В число трех наиболее рискованных параметров входят цена на готовую продукцию, себестоимость по прямым затратам и производственные простои в силу недостатков сбыта готовой продукции.
Представленный анализ инвестиционного риска путем корректировок параметров проекта, несмотря на относительную простоту и наглядность, имеет ограничение, уменьшающее возможность его использования на практике. Можно применять сценарийно-корректировочный метод анализа, при котором порядок вероятностной оценки вариантов развития инвестиционного проекта устанавливается экспертами. Такой подход позволит получить более объективные результаты.
| Наименование параметра | Значение инвестиционной функции | АСi | RCi | |
|---|---|---|---|---|
| до | после | |||
| 7. Цена на готовую продукцию | 7 731 800 | 6 006 980 | -1 724 820 | -22,31% |
| 5. Себестоимость по прямым затратам | 7 731 800 | 6 818 660 | -913 140 | -11,81% |
| 4. Производственные простои в силу недостатков сбыта | 7 731 800 | 7 549 400 | -182 400 | -2,36% |
| 1. Сроки регистрации, получения лицензии или разрешений | 7 731 800 | 7 566 920 | -164 880 | -2,13% |
| 2. Сроки строительства и/или поставки, монтажа оборудования | 7 731 800 | 7 608 140 | -123 660 | -1,60% |
| 6. Накладные расходы | 7 731 800 | 7 674 800 | -57 000 | -0,74% |
| 3. Производственные простои в силу технических причин | 7 731 800 | 7 718 120 | -13 680 | -0,18% |
Корректировка на искажения в системе бухгалтерского учета также относится к первой группе методов анализа и регулирования инвестиционных проектов (см. табл. 3.34).
В экономическом анализе, в том числе и в инвестиционном, основной информационной базой служат данные, получаемые из системы бухгалтерского учета. В то же время следует заметить, что бухгалтерский учет как объективный способ отражения экономической реальности имеет ярко выраженный национальный характер и сильно различается в разных странах. Ведущаяся в течение последних лет работа по внедрению международных стандартов бухгалтерского учета на практике сталкивается с определенными сложностями. Российская Федерация проводит активную политику формального перехода на международные стандарты бухгалтерского учета. В то же время наметились и отрицательные тенденции в развитии этого направления. Ориентация бухгалтерского учета на вопросы налогов привела к тому, что бухгалтерская отчетность зачастую не отражает реальных экономических процессов. Остается еще достаточное количество нормативных требований, несовместимых с нормами рыночной экономики. Примером может служить централизованное утверждение форм первичных документов, государственное регулирование формирования себестоимости, учета инвестиций. Подобная система бухгалтерского учета не всегда может служить инструментом инвестиционного экономического анализа. Допускаемые расхождения в учете носят характер ярко выраженного информационного риска. В силу тотального информационного дефицита и уклонения от налогообложения эти риски достаточно велики. Если уверенности в корректности финансовых отчетов нет, предлагается не рассматривать бухгалтерские сведения, а ограничиться непосредственным сбором и анализом пусть косвенной, но подтверждаемой документально или физически информации.
Укрупненная оценка устойчивости (см. табл. 3.34) основывается на разработке так называемых сценариев развития проекта в базовом и других вариантах. По каждому сценарию исследуется, как в соответствующих условиях будет действовать организационно-экономический механизм реализации проекта, какими будут показатели эффективности. Влияние факторов риска на норму дисконта при расчетах не учитывается. Проект будет считаться устойчивым и эффективным, если во всех рассмотренных ситуациях интересы участников соблюдаются, а нежелательные последствия устраняются за счет управления рисками. Достоинством метода является то, что он позволяет оценить одновременное влияние нескольких параметров на конечные результаты проекта через вероятность наступления каждого сценария.
Метод использования аналогов (см. табл. 3.34) заключается в поиске и использовании сходства, подобия явлений (проектов) и их сопоставлении с другими аналогичными объектами. Для этого метода, как и для метода экспертных оценок, характерен определенный субъективизм, так как решающее значение при оценке объектов имеют интуиция, опыт и знания эксперта или аналитика.
Ко второй группе методов анализа и регулирования риска инвестиционных проектов отнесены методы средней математической сложности (см. табл. 3.34).
В теории известны и относительно широко применяются на практике такие методы как метод экспертных оценок, "дерево решений", анализ чувствительности проекта. К менее известному, но достаточно мощному и простому инструменту анализа относится метод составления и анализа балансов коммерческой организации (предприятия) с учетом будущего прироста активов и связанного с этим риска.
Экспертный метод часто выступает не в роли самостоятельного метода анализа инвестиционного риска, а в качестве инструмента получения информации в слабоформализованных моделях. Этот метод основан на анкетировании специалистов-экспертов и дальнейшей обработке их мнений. Желательно, чтобы специалисты давали свои оценки вероятностей возникновения уровней потерь. Можно ограничиться получением оценок вероятностей допустимого и критического рисков. Можно поставить перед экспертами вопрос: какие потери наиболее вероятны в данном виде деятельности? Полученные результаты оценок обрабатываются в соответствии с поставленной аналитической задачей. Опрос экспертов и анализ согласованности их мнений достаточно широко освящен в литературе.
Метод построения и анализа "дерева решений" рассматривается в специальной литературе. Аналитик проекта, который строит "дерево решений", должен иметь максимум информации, чтобы представлять возможные сценарии развития проекта с учетом вероятности и времени их наступления. Узлы "дерева решений" представляют собой ключевые события, а стрелки, соединяющие их, - проводимые работы по реализации проекта. В итоге приводится информация относительно времени, стоимости работ и вероятности принятия того или иного решения. Определяется чистый дисконтированный доход (ЧДД) по каждому сценарию, а также интегральный показатель ЧДД. Положительная величина интегрального показателя указывает на приемлемую степень риска, связанного с реализацией проекта.
В практической деятельности метод построения дерева решений используется относительно редко, несмотря на очень добротную математическую модель. Возникают большие трудности в описании проектов с точки зрения четко определенных альтернатив на нескольких этапах его развития, а также математических ожиданий и вероятностей подобных исходов.
Анализ чувствительности - один из наиболее распространенных методов исследования инвестиционных рисков. Практически каждое пособие в области инвестиционного проектирования упоминает данный метод. Этот анализ помогает более точно оценить, насколько сильно изменится эффективность при определенном изменении одного из исходных параметров проекта. Чем сильнее эта зависимость, тем выше риск реализации проекта.
Предполагается применять анализ чувствительности проекта в двух случаях:
- для определения факторов, оказывающих наиболее сильное влияние на результаты проекта;
- для сравнительного анализа проектов - как повлияет изменение труднопрогнозируемых факторов на эффективность проекта.
При применении сложных математических методов, в том числе и такого, как "энтропия инвестиционного проекта" (см. табл. 3.34), часто проводится предварительный анализ чувствительности (см. далее по тексту).
Составление и анализ балансов предприятия с учетом будущего прироста активов и связанного с ним риска также являются одним из направлений (методов) анализа и регулирования риска инвестиционных проектов (см. табл. 3.34). Это так называемый метод составления риск-балансов.
Рассмотреть использование данного метода можно с позиции бухгалтерского учета - универсальной системы фиксации фактов экономического характера, в основе которой лежит баланс имущества предприятия (активы) и юридических прав на него в форме долгов и собственного капитала (пассив баланса) (см. табл. 3.38).
| Активы (имущество организации) | Пассивы (юридические права на имущество) | ||
|---|---|---|---|
| Внеоборотные активы | 1 200 | Долги | 600 |
| Оборотные активы | 3 500 | Собственный капитал | 2 600 |
| Нераспределенная прибыль | 1 500 | ||
| Итого активы (баланс) | 4 700 | 4 700 | |
Заметим, что под долгами понимается задолженность по всем основаниям. Имеющееся равенство активов и пассивов объясняется необходимостью наличия для каждого вида имущества каких-либо прав на него, а реализуется путем механизма двойной записи (double entry). Двойная запись - одновременная запись по двум пунктам (бухгалтерским счетам) активов и пассивов либо перераспределение средств внутри активов или пассивов. Технически это выполняется с помощью бухгалтерской проводки - однократной записи по двум счетам. При этом каждая хозяйственная операция имеет направления получения средств (Дебет в проводке) и источник данных средств (Кредит).
Методологической основой составления риск-балансов является ввод в состав активов и пассивов статей баланса, отражающих будущий прирост активов и пассивов, вызванных реализацией инвестиционного проекта (см. табл. 3.39).
| Активы (имущество организации) | Пассивы (юридические права на имущество) | ||
|---|---|---|---|
| Внеоборотные активы | 1 200 | Долги | 600 |
| Оборотные активы | 3 500 | Собственный капитал | 2 600 |
| Нераспределенная прибыль | 1 500 | ||
| Будущий прирост активов | 2 000 | Будущие рисковые потери | 2 000 |
| Сторно будущего прироста активов | -2 000 | Сторно будущих рисковых потерь | -2 000 |
| Итого активы (баланс) | 4 700 | Итого пассивы (баланс) | 4 700 |
В активах баланса отражен возможный прирост имущества предприятия, а в пассиве - возможные рисковые потери, в данном случае играющие роль потенциальной прибыли. Достичь этого стало возможно при введении в состав бухгалтерских счетов активного счета "Будущий прирост имущества", пассивного счета "Будущие рисковые потери" и контрарных (противоположных) к ним счетов - "Сторно будущего прироста активов" и "Сторно будущих рисковых потерь". При приравнивании суммы имущества и резервов под его потери итог первоначального баланса не изменится. Прирост активов и пассивов в сумме составляет ноль. Сумма активов и пассивов (валюта баланса) будет соответствовать финансовому положению предприятия на момент реализации инвестиционного проекта. Например, будущий инвестиционный проект предполагает номинальный прирост имущества на 2000 денежных единиц, при этом будущие рисковые потери составят точно такую же сумму.
В рамках представления информации о выгодах и рисках инвестиционного проекта не учитываются вопросы, связанные с определением относительной степени риска проекта, сроков его выполнения, и не принимается во внимание ценность денег во времени. Эти недостатки в какой-то мере могут быть устранены при разбиении счетов "Будущий прирост активов" и "Будущие рисковые потери" на составляющие (субсчета).
Недостатком метода является то, что в предлагаемых балансах отражается ситуация, которая была в начале осуществления инвестиционного проекта. Важно, чтобы в любой момент времени на всем протяжении реализации проекта риск-баланс отражал соотношение между будущим приростом активов и будущими рисковыми потерями в той части проекта, в какой он еще не реализован. Это позволит создать достаточно наглядный и очевидный инструмент мониторинга реализации инвестиционного проекта.
Составление баланса с введением будущего прироста активов и рисковых потерь выходит за пределы бухгалтерского учета в его существующем нормативном понимании и требует ведения специального управленческого финансового учета. Это позволит создать некоторый механизм управления рисками.
К третьей группе отнесены методы, чья математическая составляющая имеет максимальную степень сложности. Виды основных методов указаны в представленной классификации (см. табл. 3.34). Каждый из них достаточно широко рассматривается в теории и представляет собой синтез методов теории вероятности, математической статистики, теории игр и исследований операций. В теории статистических решений обычно используются принципы Байеса, Бернулли и энтропии математического ожидания функции полезности.
Методы третьей группы применяются на практике относительно редко. Это связано со сложностью построения математических моделей и работы с ними, отсутствием соответствующего программного обеспечения. Методы расчета уровня риска требуют наличия большого объема информации, которой не всегда обладает инициатор проекта (инвестор). В то же время использование рассматриваемых методов может существенно повысить качество экономического анализа инвестиционных рисков.
При реализации планов долгосрочного инвестирования неизбежно сталкиваются с неопределенностью показателей по затратам и результатам. Деление риска на собственно риск и неопределенность как вид риска, вероятность которого определить невозможно - нецелесообразно. Вероятность возникновения риска практически всегда определяется на основании тех или иных допущений. При этом различия между неопределенностью и риском в большей степени становятся качественными, нежели количественными. Возникает проблема измерения риска и его влияния на результаты инвестиции.
В методических рекомендациях при расчетах эффективности предлагают учитывать неопределенность, т.е. неполноту и неточность информации. В условиях неопределенности возможно использовать следующие методы оценки проектных рисков:
- укрупненная оценка устойчивости;
- расчет уровня безубыточности;
- метод вариации параметров;
- оценка ожидаемого эффекта проекта с учетом количественных характеристик неопределенности.
Формализованное описание неопределенности является наиболее точным и одновременно наиболее сложным с технической точки зрения методом. Применительно к видам неопределенности этот метод включает следующие этапы:
- описание всего множества возможных условий реализации проекта в форме соответствующих сценариев или моделей, учитывающих ограничения на значения основных параметров проекта;
- определение затрат и результатов;
- преобразование исходной информации о факторах неопределенности в информацию о вероятностях отдельных условий реализации проекта и соответствующих показателей эффективности;
- определение показателей эффективности проекта в целом, с учетом неопределенности условий его реализации.
Если вероятности различных условий реализации проекта известны, по формуле математического ожидания определяется ожидаемый интегральный эффект:
Эож = Э x Р,
| где | Эож | - | ожидаемый интегральный эффект; |
| Э | - | интегральный эффект при условии реализации; | |
| Р | - | вероятность реализации этого условия. |
Если непосредственно измерить размеры потерь или их вероятностей невозможно, проводят ранжирование соответствующих объектов или процессов в отношении возможного ущерба, потерь и т.д. Это ранжирование часто основывается на экспертных суждениях. Все количественные данные в той или иной степени должны характеризовать общий абсолютный риск, общий относительный риск, общий показатель рисковой устойчивости инвестиционного проекта либо их сочетание. Покажем это на примере.
Пусть дан некий инвестиционный проект А. При этом существует достаточно большой теоретический ряд инвестиционных проектов Аj, достаточно схожих с проектом А, далее называемым Аi, чтобы фактический интегральный показатель IF данного проекта Аi был равен математическому ожиданию таких показателей теоретического ряда проектов Аj:
IF(Ai) = Mi[IF(Aj)].
При этом математическое ожидание Mi[IF(Aj)] определяется как сумма произведений вероятностей P(Aj) на величину IF(Aj), т.е. теоретический ряд в данном представлении - дискретное распределение с законом, близким к нормальному:
![M_i [IF(A_j)] = \Sigma IF(A_j) x P[IF(A_j)]](/sites/default/files/tex_cache/b3b0044fb574378e0dfc804a486becd2.png) .
.
Общий абсолютный инвестиционный риск может быть определен как среднеквадратичное отклонение ряда Аj, численно равное корню квадратному из суммы произведения квадрата разницы между математическим ожиданием, j-значением ряда и вероятности данного значения:
Таким образом, общий абсолютный инвестиционный риск  проекта А равен среднеквадратичному отклонению интегральных показателей достаточно большого ряда гипотетических проектов Аj, настолько близких к исследуемому, чтобы математическое ожидание интегральных показателей данных проектов Mi[IF] было равно интегральному показателю исследуемого инвестиционного проекта IF(Aj).
проекта А равен среднеквадратичному отклонению интегральных показателей достаточно большого ряда гипотетических проектов Аj, настолько близких к исследуемому, чтобы математическое ожидание интегральных показателей данных проектов Mi[IF] было равно интегральному показателю исследуемого инвестиционного проекта IF(Aj).
Общий относительный показатель инвестиционного риска ri может быть найден как коэффициент вариации ряда гипотетических проектов Аj и определен как отношение среднеквадратичного отклонения интегральных показателей достаточно большого ряда гипотетических проектов Аj к математическому ожиданию интегральных показателей данных проектов Mi[IF]:
Общий показатель устойчивости к риску R инвестиционного проекта А возможно определить как разницу между единицей и коэффициентом вариации ri ряда гипотетических проектов Аj:
Ri = 1 - ri.
Общий абсолютный показатель инвестиционного риска характеризует возможные средние потери в ходе реализации инвестиционного проекта. Его величина - повод для сравнения с имеющимися резервами предприятия, в том числе собственными и заемными средствами.
Общий относительный риск инвестиционного проекта характеризует относительный разброс возможных значений - вариацию возможных исходов. Данный показатель практически незаменим при сравнении конкурирующих инвестиционных проектов.
Общий показатель устойчивости инвестиционного проекта к риску описывает относительную неизменность среднего исхода инвестиционного проекта.
Представленная формализация общих понятий инвестиционного риска и подходов его определения крайне важна в плане рассмотрения методов оценки проектного риска.
Дисперсионный и иной статистический анализ (см. табл. 3.34) может быть проведен как анализ результатов некоторого процесса в зависимости от тех или иных факторов, с применением методов теории вероятности и математической статистики. С помощью статистических методов могут быть исследованы доходы и потери от вложения капитала и установлена частота их возникновения. В процессе применения статистического метода рассчитываются среднеквадратическое (стандартное) отклонение, дисперсии, коэффициент вариации. В теории финансов дисперсия и стандартное отклонение часто используются для измерения риска. Чем они выше, тем более рискованным считается данный вид деятельности.
Показатель среднеквадратического отклонения ( ¯) по инвестиционному проекту рассчитывают по формуле:
¯) по инвестиционному проекту рассчитывают по формуле:
| где | t | - | число периодов (мес., лет); |
| n | - | число наблюдений; | |
| Дi | - | расчетный доход по инвестиционному проекту i-го вида при различных значениях конъюнктуры на рынке инвестиционных товаров; | |
| Д¯ | - | средний ожидаемый доход (чистый денежный поток, дп); | |
| Рi | - | значение вероятности, которое соответствует расчетному доходу (общая величина р = 1), доли единицы. |
Значение Рi устанавливают экспертным путем.
Вариация выражает изменения (колебаемость) количественной оценки признака при переходе от одного случая (варианта) к другому. Коэффициент вариации (kв) позволяет оценить уровень риска, если показатели средних ожидаемых доходов по проектам отличаются между собой:
При сравнении проектов по уровню риска предпочтение отдают тому, в котором значение kв является минимальным. В этом случае достигается наиболее благоприятное соотношение риска и дохода.
Статистический метод требует наличия значительного массива данных, которые далеко не всегда имеются в распоряжении.
Одним из подходов к анализу и регулированию инвестиционного риска является применение имитационных моделей (см. табл. 3.34). Среди них можно выделить три наиболее распространенных вида: модель оценки капитальных активов (САРМ - capital assets pricing model), модель оценки опционов (ОРТ - option pricing theory) и метод Монте-Карло.
Применение в российских условиях двух первых моделей практически невозможно. Они разработаны на основе близкого сходства между инвестициями в реальный сектор и на рынке акций. В России отсутствует эффективный рынок капиталов, а массовое инвестирование осуществляется относительно небольших средств.
Относительно широко известен метод Монте-Карло, для которого разработано соответствующее программное обеспечение. Это метод формализованного описания неопределенности, используемый в наиболее сложных для прогнозирования проектах. Его сущность заключается в многократном повторении некоторого опыта и выявлении на этой основе устойчивых тенденций развития неизвестного, но смоделированного процесса. Метод основан на применении имитационных моделей, которые согласуются с заданными ограничениями на исходные переменные. При этом в качестве ожидаемого интегрального эффекта проекта рассматриваются чистый дисконтированный доход, интегральный эффект и другие показатели. Совершенствование метода может идти по пути массового внедрения программного обеспечения и определения его особенностей в анализе проектных рисков на основе сложившейся практики.
К одному из относительно новых методов анализа и регулирования инвестиционного риска можно отнести (при определенных условиях) метод энтропии инвестиционного проекта (см. табл. 3.34). Термин "энтропия" используется в теории неопределенности, теории информации и математической статистики и означает неопределенность, количественную меру неупорядоченности. Практически все расчеты энтропии могут быть выполнены в обычной электронной таблице Microsoft Excel - 95/97/2000. Однако соответствующий рисковый инструментарий в специальных программных пакетах выражен относительно слабо. Возможно и необходимо расширить метод энтропии и использовать его как один из сложных математических методов анализа и регулирования инвестиционного риска. Понятие энтропии инвестиционного проекта должно рассматриваться как вероятность достижения его интегрального показателя некого критического уровня, например, вероятности его убыточности. Подобную энтропию будут характеризовать два показателя риска: общий показатель устойчивости риска и общий относительный показатель инвестиционного риска. Существуют и другие требования и допущения, которые должны учитываться при использовании этого метода.
Более полно сущность метода энтропии инвестиционного проекта раскрывается при представлении всей системы расчетов в определенной последовательности, состоящей из следующих этапов.
Этап 1. Подготовка рядов анализа чувствительности с экспертными оценками.
Метод энтропии является продолжением и развитием метода анализа чувствительности инвестиционного проекта, который отнесен к группе методов средней сложности (см. табл. 3.34). Подготовка рядов анализа чувствительности начинается с выбора ведущих (основных) факторов энтропийного анализа. Предлагается проводить отбор факторов с учетом специфики конкретного инвестиционного проекта и при условии соблюдения соответствующих требований. Как правило, выделяют два важных требования.
Во-первых, выбранные факторы должны составить полную группу событий, т.е. описать все возможные изменчивые факторы. Принимая во внимание то, что причин (факторов), влияющих на инвестиционный проект, очень много, целесообразно подобрать такие из них, которые с той или иной достоверностью описывают почти всю социально-экономическую неопределенность инвестиционного проекта. Соблюдение этого требования крайне важно для получения объективного конечного результата. В то же время из-за сложности расчетов к анализу часто принимают не более четырех факторов. Факторы, не принятые к рассмотрению, должны иметь небольшую вариацию.
Второе требование заключается в том, чтобы ряды данных анализа не обладали парной или множественной коррелированностью, т.е. показатели не были взаимно зависимыми. Все процессы пронизаны сложными связями, и в чистом виде это требование трудно выполнимо. Необходимо, чтобы взаимные связи не были такими явными, но тем не менее присутствовали.
В итоге можно заключить, что метод энтропии инвестиционного проекта применим при условии соблюдения одного из важных допущений, когда группа i-х факторов описывает полную группу возможных гипотез, не коррелирующих между собой. Это допущение соблюдается путем правильного и взвешенного набора i-х факторов и обусловлено требованиями формулы полной вероятности, на основе которой рассчитывается энтропия EN. Теоретическое обоснование данного положения дано в работе.
В состав номенклатуры факторов (показателей) для энтропийного анализа могут быть включены:
- чистый дисконтированный доход;
- норма расхода материала и цена на i-й вид материала;
- уровень (размер) общепроизводственных, общехозяйственных и коммерческих расходов;
- расходы на оплату труда;
- объем продаж;
- средние размеры складских запасов;
- оборачиваемость дебиторской задолженности;
- процентные ставки по кредитам, займам и для размера дисконта;
- размеры инфляции.
После установления номенклатуры факторов определяется интегральный показатель эффективности инвестиционного проекта при изменении каждого фактора и неизменности других. В качестве такого показателя можно принять, например, чистый дисконтированный доход (ЧДД).
При проведении соответствующих расчетов интегрального показателя используем метод анализа чувствительности инвестиционного проекта. Будем исходить из того, что этот анализ ориентирован на исследование внутренней структуры, восприимчивости проекта к проявлениям того или иного риска. Подобный анализ выявляет соотношение изменений одного или нескольких факторов и изменение интегрального показателя инвестиционного проекта и генерации выводов на основе таких соотношений.
Пример ряда анализа чувствительности для одного из факторов представлен в табл. 3.40.
| +50% | +40% | +30% | +20% | +10% | 0 | |
| Инвестиции, тыс. руб. | 15 000 | 14 000 | 13 000 | 12 000 | 11 000 | 10 000 |
| Чистый дисконтированный доход (NPV), тыс. руб. | 25 000 | 26 000 | 27 000 | 28 000 | 29 000 | 30 000 |
| -10% | -20% | -30% | -40% | -50% | ||
| Инвестиции, тыс. руб. | 9 000 | 8 000 | 7 000 | 6 000 | 5 000 | |
| Чистый дисконтированный доход (NPV), тыс. руб. | 31 000 | 32 000 | 33 000 | 34 000 | 35 000 |
Далее экспертно оценивается изменение принятого фактора, определяется вероятность каждого изменения. Пусть такая вероятность опосредовано выражается в виде балла ni для i-го варианта. В этом случае вероятность можно рассчитать как удельный вес изменения фактора по следующей формуле:
Взвешенный ряд чувствительности можно отразить в следующей таблице.
| +50% | +40% | +30% | +20% | +10% | 0 | |
| Фактор | Чистый дисконтированный доход | |||||
| NVP | ||||||
| Балльная оценка, ni | 1 | 2 | 3 | 3 | 5 | 5 |
| Вероятность, Pi | 0,0385 | 0,0769 | 0,1154 | 0,1154 | 0,1923 | 0,1923 |
| -10% | -20% | -30% | -40% | -50% | ||
| Фактор | Чистый дисконтированный доход | |||||
| NVP | Сумма | |||||
| Балльная оценка, ni | 4 | 2 | 1 | 1 | 0 | 26 |
| Вероятность, Pi | 0,15 39 | 0,07 69 | 0,03 85 | 0,03 85 | 0 | 100% |
Этап 2. Обработка рядов анализа чувствительности
Проводится обработка каждого взвешенного ряда. Определяется статистическое распределение, требующее тщательного расчета и анализа критериев согласия.
Широкое использование в математической статистике плотности распределения обусловлено тем, что в рассматриваемом ряде анализа чувствительности оперировать этими категориями проще и удобнее. Случайные распределения описываются рядом числовых характеристик, основные из которых: математическое ожидание, дисперсия и среднеквадратическое отклонение.
Математическое ожидание (М [x], m) случайной величины - среднее ее возможных значений. Для дискретной статистической совокупности математическое ожидание равно взвешенной средней всех вариантов:
![M[x] = \sigma x_i p_i](/sites/default/files/tex_cache/5bbf9294985554198f8a333c5773fb71.png) .
.
Для непрерывной случайной величины математическое ожидание приобретает интегральный вид:
Дисперсия случайной величины характеризует разброс значений случайной величины. Дисперсия численно равна математическому ожиданию квадрата разности между значением случайной величины и ее математического ожидания:
![D[x] = M[(x - M)^2]](/sites/default/files/tex_cache/a2eb62996f4177e68530e3dba7cdf66a.png) ;
;
![D[x] = \sigma (x_i - M)^2 xp_i](/sites/default/files/tex_cache/f9b6f91b3e6f108cb07bfc750e6dd6cb.png) ;
;
Размерность дисперсии - квадрат размерности случайной величины. Для совпадения размерности из дисперсии извлекают квадратный корень и получают среднеквадратичное отклонение:
Среднеквадратичное отклонение численно равно среднему отклонению значения ряда от средней ряда. Для перехода к безразмерным величинам следует использовать один из наиболее распространенных показателей колеблимости статистической совокупности - коэффициент вариации. Этот коэффициент равен отношению среднеквадратичного отклонения к математическому ожиданию:
Коэффициент вариации позволяет оценивать по степени риска несхожие статистические совокупности, например разновеличинные или разноразмерные.
Для каждого энтропийного фактора по следующей схеме составляется таблица предварительного расчета (см. табл. 3.42).
Сумма строки (4) в табл. 3.42 дает показатель математического ожидания m средней взвешенной на вероятности (экспертные баллы возможности появления того или иного варианта). Сумма строки (5) равна дисперсии статистической совокупности NPVij. Квадратный корень из дисперсии дает среднеквадратичное отклонение статистической совокупности 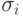 .
.
| Наименование | j-е значения i-го фактора | Всего | |||||
| 1. NPVij.
2. Экспертный балл, nij. 3. Вероятность j-го варианта, Pij. 4. Стр. 1 x стр. 3. 5. Квадрат отклонения NPVij от среднего, взвешенный на вероятность |
|||||||
После проведения всех указанных расчетов проверяется соответствие данных статистической совокупности на нормальность (соответствие нормальному закону распределения). Этот закон выбирается в силу своей распространенности и методической проработанности, он предусматривает сосредоточенность "в основном" вокруг математического ожидания. В то же время это свойственно не всем факторам инвестиционного проекта. Данные распределения требуют проверки соответствующими критериями согласия. В энтропийном анализе возможно применение и иных законов распределения. Например, закона редких событий, распределения Пуассона.
При успешной проверке согласия гипотезы строится статистическое распределение по нормальному (или иному) закону. Метод энтропии инвестиционного проекта применим при условии, когда iе статистические распределения статистически состоятельны, т.е. обладают репрезентативностью и согласованы с теоретическими законами распределения.
Этап 3. Подготовка к расчету энтропии.
На этом этапе расчетов полученные данные статистических распределений используются для определения критического уровня отклонения интегрального показателя инвестиционного проекта. Данные вероятности усредняются, и возникает вероятность достижения проектом критического уровня интегрального показателя, называемого энтропией инвестиционного проекта.
Если за интегральный показатель эффективности инвестиционного проекта принять чистый дисконтированный доход (ЧДД), критическим уровнем будет тот размер ЧДД, который может привести к отказу от реализации проекта. Данный размер должен определяться исходя из предпочтений и требований сторонних финансовых посредников, акционеров, руководства. К требованиям критического уровня требуется подходить осторожно. Проблему можно решить, если представить энтропию не в виде точечного значения, а в виде дискретного распределения, где частотами служит размер критического уровня в процентах от расчетного. Приведем пример.
Пусть ЧДД проекта согласно расчета составляет 180 денежных единиц. Суммируя вышеперечисленные требования, принимаем, что если потери в ЧДД с высокой степенью вероятности составят 30% и более, от реализации инвестиционного проекта желательно отказаться. В этом случае критический уровень ЧДД составит 126 денежных единиц (180-30%). Распределение энтропии и критического уровня инвестиционного проекта может быть представлено следующим образом.
| Наименование показателя | Значение показателя | ||||
| Критический уровень интегрального показателя инвестиционного проекта | -10% | -20% | -30% | -40% | -50% |
| Энтропия инвестиционного проекта | 42% | 34% | 21% | 16% | 9% |
Из таблицы 3.43 видно, что энтропия выступает как убывающая функция от величины модуля критического уровня. Определяется вероятность достижения критического уровня для каждого i-го фактора инвестиционного проекта Pi. Рассчитываются коэффициенты вариации (Vi) для каждого из рядов, определяющие вероятность появления данной, i-й, гипотезы. Все полученные результаты оформляются в таблице промежуточного расчета.
Этап 4. Расчет энтропии.
Энтропия инвестиционного проекта EN (вероятность достижения проектом критического уровня) определяется как средняя взвешенная вероятностей Pi, где в качестве весов выступают коэффициенты вариации Vi:
Последним шагом расчетов является определение вклада каждого фактора в формирование энтропии. Ряды ранжируются по коэффициентам вариации. Факторы соответственно показывают их участие в риске достижения проектом критических показателей. Результаты представляются в виде списка наиболее рисковых факторов инвестиционного проекта.
Контрольные вопросы
- Охарактеризуйте стратегическое планирование производства (круг проблем; цели и задачи, решаемые при планировании).
- Каковы основные этапы процесса стратегического планирования, дайте краткую характеристику каждого этапа.
- Что представляет собой процесс стратегического планирования новой продукции, как отражается конкретная стратегия при формировании инвестиционных проектов и бизнес-планировании.
- Дайте характеристику стратегического планирования потребности ресурсов, определения потребности ресурсов, определения потребности в инвестициях, сопоставления капитальных затрат разных лет.
- Перечислите факторы риска, показатели и методы оценки риска при стратегическом планировании производства.
- В чем заключается сущность ценовой стратегии, каковы этапы процесса ценообразования, уровень продажной цены продукта?
- Перечислите методы оценки стратегии развития предприятия и направления их совершенствования.
- Укажите признаки, лежащие в основе классификации методов разработки, оценки и корректировки стратегического плана. Какие группы методов могут быть использованы применительно к тому или иному признаку?
- Что представляет собой планирование стратегии, инноваций и инвестиций в общем процессе стратегического планирования?
- Каким по содержанию должен быть инновационный бизнес-план предприятия, занятого производственной деятельностью?