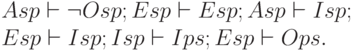Силлогистика Аристотеля
Законы силлогистики
Любой вывод, представимый в силлогистике Аристотеля, может иметь или не иметь посылок. По числу используемых посылок можно различать выводы ранга 0, 1, 2 и т.д.
Утверждения, для которых посылки не нужны, называются законами силлогистики (в некоторых логических системах они называются аксиомами). Таких законов в силлогистике Аристотеля три: закон тождества, закон противоречия и закон исключённого третьего.
Прежде чем перейти к их формулировкам, введём обозначения, восходящие к Петру Испанскому, жившему в XIII веке и написавшему широко распространённое в Средние века сочинение, в котором излагалась логика Аристотеля с возникшими к тому времени добавлениями.
Эти обозначения (породившие кванторы в современной математической логике), следующие:
А – Всякий + есть +. Е – Всякий + не есть +. I – Некоторый + есть +. О – Некоторый + не есть +.
В этих записях знак плюс означает свободное место, на которое можно поставить имя некоторого конкретного класса сущности. В первой позиции этот класс играет роль класса S, а во второй – Р. Тогда условимся для удобства записи конкретные классы обозначать малыми буквами s и р.
Введём ещё один символ, называемый знаком выводимости 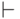 . Запись
. Запись 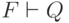 означает, что если относительно всех посылок, входящих в совокупность F, известно, что они выводимы, то заключение Q также выводимо. Запись
означает, что если относительно всех посылок, входящих в совокупность F, известно, что они выводимы, то заключение Q также выводимо. Запись 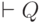 означает, что Q выводимо всегда и не зависит от выводимости каких-то других утверждений. Это вывод нулевого ранга, т.е. закон силлогистики (мы говорим: принимаем за аксиому).
означает, что Q выводимо всегда и не зависит от выводимости каких-то других утверждений. Это вывод нулевого ранга, т.е. закон силлогистики (мы говорим: принимаем за аксиому).
Закон тождества формулируется следующим образом: всякий s есть s, или, в принятых обозначениях
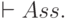
Смысл закона состоит в утверждении, что всякая конкретная сущность, входящая в класс S, обладает всеми свойствами элементов этого класса. Формально представляется, что в таком утверждении нет смысла. Однако в человеческом общении оно несёт не информационную, а эмоциональную нагрузку. "Осень есть осень", - говорим мы. "Да, ненастье есть ненастье", - отвечает собеседник.
Для формулировки следующих законов введём две логические связки – конъюнкцию, которую будем обозначать &, и дизъюнкцию, которую будем обозначать 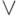 . Смысл их состоит в том, что сложное утверждение F1 & F2 истинно лишь тогда, когда истинны оба утверждения F1 и F2, а утверждение
. Смысл их состоит в том, что сложное утверждение F1 & F2 истинно лишь тогда, когда истинны оба утверждения F1 и F2, а утверждение 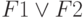 истинно в том случае, если истинно хотя бы одно из них. Пусть обозначение
истинно в том случае, если истинно хотя бы одно из них. Пусть обозначение 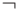 интерпретируется в записи вида
интерпретируется в записи вида 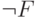 как утверждение о том, что неверно, что F является истинным.
как утверждение о том, что неверно, что F является истинным.
Тогда закон противоречия записывается следующим образом:
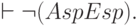
Это означает, что невозможна ситуация, когда конкретные сущности из класса S одновременно входят в р и не входят в него.
Известный поэт, "генерал" поэзии того времени, придрался к автору слов песни "Бухенвальдский набат" Исааку Соболеву:
Сотни тысяч заживо сожжённых
Строятся, строятся в шеренги к ряду ряд.
Действительно, как могут строиться мёртвые? Поэт песни (композитор Ванно Мурадели), облетевшей весь мир, остался тщательно скрываем и умер в болезнях и нищете. Конечно, эти слова поэта явились поводом при гонениях "неудобного" правдолюбца, но мы могли бы воскликнуть: "Силлогистику – на службу коммунизма!"
Ещё большую критику может вызвать закон исключённого третьего, записываемый следующим образом:
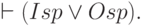
Он говорит, что для каждой конкретной сущности а, входящей в s, истинно одно из двух утверждений "а входит в р" или "а не входит в р" (третьего не дано). Совместно эти два утверждения не могут быть истинными, что следует из закона противоречия. Закон исключённого третьего в процессе развития логики подвергается постоянной критике, ибо вся человеческая практика пронизана примерами его невыполнения. Из конструктивной логики этот закон исключён.
Геометрические теоретико-множественные (жергоновы) соотношения, следующие из рис. 2.1, позволяют написать несколько примеров вывода первого ранга, т.е. с одной посылкой, истинность которой является достаточным условием для истинности заключения. Справедливость вывода непосредственно следует из рисунка и таблицы, задающей условия истинности для схем базовых высказываний.
Эти примеры следующие: