Реализация некоторых численных методов

8.1.4 Модифицированный метод Ньютона (метод секущих)

В этом методе для вычисления производных на каждом шаге поиска используется численное дифференцирование по формуле:

Тогда рекуррентная формула метода Ньютона приобретёт вид:

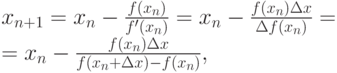
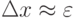Реализация данного метода в Maxima представлено ниже:

(%i1)	secant(f,sp,eps):=block([x0,x1,d,y,r],
	x0:sp[1],x1:sp[2],
	p:0, r:x1-x0, d:float(subst(x0,x,f)),
	while abs(r)>eps do (
		p:p+1, y:float(subst(x1,x,f)), r:r/(d-y)*y,
		d:y, x1:x1+r
	),
	x1)$
(%i2)	f:exp(-x)-x$
	eps:0.000001$ xrez:secant(f,[-2,2],eps)$
	print("Решение ",xrez," Невязка ",subst(xrez,x,f))$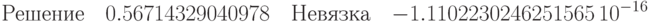

Особенности программирования для Maxima, использованные в этом примере, аналогичны приведённым выше в примере, касающемся метода половинного деления.

8.1.5 Метод хорд

Метод основан на замене функции на каждом шаге поиска хордой, пересечение которой с осью дает приближение корня.

При этом в процессе поиска семейство хорд может строится:

1. при фиксированном левом конце хорд, т.е. 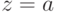, тогда начальная точка ;
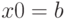2. при фиксированном правом конце хорд, т.е. 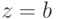, тогда начальная точка .

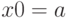В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:

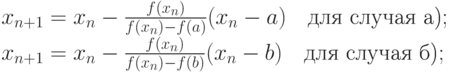
Процесс поиска продолжается до тех пор, пока не выполнится условие

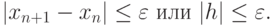
Метод обеспечивает быструю сходимость, если 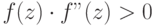, т.е. хорды фиксируются в том конце интервала , где знаки функции 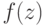и ее кривизны 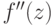совпадают.