|
Добрый день! Подскажите пожалуйста как и когда получить диплом, после сдичи и оплаты????? |
Алгоритмы симметричного шифрования. Часть 1
Сеть Фейстеля
Блочный алгоритм преобразовывает n-битный блок незашифрованного текста в n-битный блок зашифрованного текста. Число блоков длины n равно 2n. Для того чтобы преобразование было обратимым, каждый из таких блоков должен преобразовываться в свой уникальный блок зашифрованного текста. При маленькой длине блока такая подстановка плохо скрывает статистические особенности незашифрованного текста. Если блок имеет длину 64 бита, то он уже хорошо скрывает статистические особенности исходного текста. Но в данном случае преобразование текста не может быть произвольным в силу того, что ключом будет являться само преобразование, что исключает эффективную как программную, так и аппаратную реализации.
Наиболее широкое распространение получили сети Фейстеля, так как, с одной стороны, они удовлетворяют всем требованиям к алгоритмам симметричного шифрования, а с другой стороны, достаточно просты и компактны.
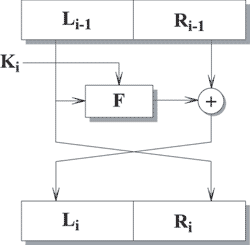
Сеть Фейстеля имеет следующую структуру. Входной блок делится на несколько равной длины подблоков, называемых ветвями. В случае, если блок имеет длину 64 бита, используются две ветви по 32 бита каждая. Каждая ветвь обрабатывается независимо от другой, после чего осуществляется циклический сдвиг всех ветвей влево. Такое преобразование выполняется несколько циклов или раундов . В случае двух ветвей каждый раунд имеет структуру, показанную на рисунке:
Функция F называется образующей. Каждый раунд состоит из вычисления функции F для одной ветви и побитового выполнения операции XOR результата F с другой ветвью. После этого ветви меняются местами. Считается, что оптимальное число раундов - от 8 до 32. Важно то, что увеличение количества раундов значительно увеличивает криптостойкость алгоритма. Возможно, эта особенность и повлияла на столь активное распространение сети Фейстеля, так как для большей криптостойкости достаточно просто увеличить количество раундов, не изменяя сам алгоритм. В последнее время количество раундов не фиксируется, а лишь указываются допустимые пределы.
Сеть Фейстеля является обратимой даже в том случае, если функция F не является таковой, так как для дешифрования не требуется вычислять F-1. Для дешифрования используется тот же алгоритм, но на вход подается зашифрованный текст, и ключи используются в обратном порядке.
В настоящее время все чаще используются различные разновидности сети Фейстеля для 128-битного блока с четырьмя ветвями. Увеличение количества ветвей, а не размерности каждой ветви связано с тем, что наиболее популярными до сих пор остаются процессоры с 32-разрядными словами, следовательно, оперировать 32-разрядными словами эффективнее, чем с 64-разрядными.
Основной характеристикой алгоритма, построенного на основе сети Фейстеля, является функция F. Различные варианты касаются также начального и конечного преобразований. Подобные преобразования, называемые забеливанием (whitening), осуществляются для того, чтобы выполнить начальную рандомизацию входного текста.
Криптоанализ
Процесс, при котором предпринимается попытка узнать Х, K или и то, и другое, называется криптоанализом. Одной из возможных атак на алгоритм шифрования является лобовая атака, т.е. простой перебор всех возможных ключей. Если множество ключей достаточно большое, то подобрать ключ нереально. При длине ключа n бит количество возможных ключей равно 2n. Таким образом, чем длиннее ключ, тем более стойким считается алгоритм для лобовой атаки.
Существуют различные типы атак, основанные на том, что противнику известно определенное количество пар незашифрованное сообщение - зашифрованное сообщение. При анализе зашифрованного текста противник часто применяет статистические методы анализа текста. При этом он может иметь общее представление о типе текста, например, английский или русский текст, выполнимый файл конкретной ОС, исходный текст на некотором конкретном языке программирования и т.д. Во многих случаях криптоаналитик имеет достаточно много информации об исходном тексте. Криптоаналитик может иметь возможность перехвата одного или нескольких незашифрованных сообщений вместе с их зашифрованным видом. Или криптоаналитик может знать основной формат или основные характеристики сообщения. Говорят, что криптографическая схема абсолютно безопасна, если зашифрованное сообщение не содержит никакой информации об исходном сообщении. Говорят, что криптографическая схема вычислительно безопасна, если:
- Цена расшифровки сообщения больше цены самого сообщения.
- Время, необходимое для расшифровки сообщения, больше срока жизни сообщения.
Дифференциальный и линейный криптоанализ
Рассмотрим в общих чертах основной подход, используемый при дифференциальном и линейном криптоанализе. И в том, и в другом случае предполагается, что известно достаточно большое количество пар (незашифрованнный текст, зашифрованный текст).
Понятие дифференциального криптоанализа было введено Эли Бихамом (Biham) и Ади Шамиром (Shamir) в 1990 году. Конечная задача дифференциального криптоанализа - используя свойства алгоритма, в основном свойства S-box, определить подключ раунда . Конкретный способ дифференциального криптоанализа зависит от рассматриваемого алгоритма шифрования.
Если в основе алгоритма лежит сеть Фейстеля, то можно считать, что блок m состоит из двух половин - m0 и m1. Дифференциальный криптоанализ рассматривает отличия, которые происходят в каждой половине при шифровании. (Для алгоритма DES "отличия" определяются с помощью операции XOR, для других алгоритмов возможен иной способ). Выбирается пара незашифрованных текстов с фиксированным отличием. Затем анализируются отличия, получившиеся после шифрования одним раундом алгоритма, и определяются вероятности различных ключей. Если для многих пар входных значений, имеющих одно и то же отличие Х, при использовании одного и того же подключа одинаковыми (Y) оказываются и отличия соответствующих выходных значений, то можно говорить, что Х влечет Y с определенной вероятностью. Если эта вероятность близка к единице, то можно считать, что подключ раунда найден с данной вероятностью. Так как раунды алгоритма независимы, вероятности определения подключа каждого раунда следует перемножать. Как мы помним, считается, что результат шифрования данной пары известен. Результаты дифференциального криптоанализа используются как при разработке конкретных S-box, так и при определении оптимального числа раундов.
Другим способом криптоанализа является линейный криптоанализ, который использует линейные приближения преобразований, выполняемых алгоритмом шифрования. Данный метод позволяет найти ключ, имея достаточно большое число пар (незашифрованный текст, зашифрованный текст). Рассмотрим основные принципы, на которых базируется линейный криптоанализ. Обозначим
| P[1], … , P[n] - незашифрованный блок сообщения. |
| C[1], … , C[n] - зашифрованный блок сообщения. |
| K[1], … , K[m] - ключ. |
![A[i, j, …, k] = A[i] \oplus A[j] \oplus … \oplus A[k]](/sites/default/files/tex_cache/7975ff6145252581c91a635e52f070ae.png) |
Целью линейного криптоанализа является поиск линейного уравнения вида
![P[\alpha_1, \alpha_2, …,\alpha_a] \oplus C[\beta_1, \beta_2, …, \beta_b] = K[\gamma_1, …, \gamma_c]](/sites/default/files/tex_cache/7c0d0a142cf25260bfb528ecfbb85178.png)
Выполняющееся с вероятностью 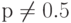 .
. 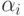 ,
, 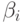 и
и 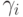 - фиксированные
позиции в блоках сообщения и ключе. Чем больше р отклоняется от 0.5,
тем более подходящим считается уравнение.
- фиксированные
позиции в блоках сообщения и ключе. Чем больше р отклоняется от 0.5,
тем более подходящим считается уравнение.
Это уравнение означает, что если выполнить операцию XOR над некоторыми битами незашифрованного сообщения и над некоторыми битами зашифрованного сообщения, получится бит, представляющий собой XOR некоторых бит ключа. Это называется линейным приближением, которое может быть верным с вероятностью р.
Уравнения составляются следующим образом. Вычисляются значения левой
части для большого числа пар соответствующих фрагментов
незашифрованного и зашифрованного блоков. Если результат оказывается
равен нулю более чем в половине случаев, то полагают, что ![K[\gamma_1, …,
\gamma_с] = 0](/sites/default/files/tex_cache/95654e3c6df79d0d9961fce73180de9b.png) . Если в большинстве случаев получается 1, полагают, что
. Если в большинстве случаев получается 1, полагают, что ![K[\gamma_1, …, \gamma_с] = 1](/sites/default/files/tex_cache/006e2cf2c217e4e82fe298e775f6cbc4.png) . Таким образом получают систему уравнений, решением
которой является ключ.
. Таким образом получают систему уравнений, решением
которой является ключ.
Как и в случае дифференциального криптоанализа, результаты линейного криптоанализа должны учитываться при разработке алгоритмов симметричного шифрования.
Используемые критерии при разработке алгоритмов
Принимая во внимание перечисленные требования, обычно считается, что алгоритм симметричного шифрования должен:
- Манипулировать данными в больших блоках, предпочтительно размером 16 или 32 бита.
- Иметь размер блока 64 или 128 бит.
- Иметь масштабируемый ключ до 256 бит.
- Использовать простые операции, которые эффективны на микропроцессорах, т.е. исключающее или, сложение, табличные подстановки, умножение по модулю. Не должно использоваться сдвигов переменной длины, побитных перестановок или условных переходов.
- Должна быть возможность реализации алгоритма на 8-битном процессоре с минимальными требованиями к памяти.
- Использовать заранее вычисленные подключи. На системах с большим количеством памяти эти подключи могут быть заранее вычислены для ускорения работы. В случае невозможности заблаговременного вычисления подключей должно произойти только замедление выполнения. Всегда должна быть возможность шифрования данных без каких-либо предварительных вычислений.
- Состоять из переменного числа итераций. Для приложений с маленькой длиной ключа нецелесообразно применять большое число итераций для противостояния дифференциальным и другим атакам. Следовательно, должна быть возможность уменьшить число итераций без потери безопасности (не более чем уменьшенный размер ключа).
- По возможности не иметь слабых ключей. Если это невозможно, то количество слабых ключей должно быть минимальным, чтобы уменьшить вероятность случайного выбора одного из них. Тем не менее, все слабые ключи должны быть заранее известны, чтобы их можно было отбраковать в процессе создания ключа.
- Задействовать подключи, которые являются односторонним хэшем ключа. Это дает возможность использовать большие парольные фразы в качестве ключа без ущерба для безопасности.
- Не иметь линейных структур, которые уменьшают комплексность и не обеспечивают исчерпывающий поиск.
- Использовать простую для понимания разработку. Это дает возможность анализа и уменьшает закрытость алгоритма.
Большинство блочных алгоритмов основано на использовании сети Фейстеля, все имеют плоское пространство ключей, с возможным исключением нескольких слабых ключей.