Теория языков

Недетерминированные и конечные автоматы

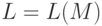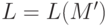Имеет место следующая теорема: если для некоторого недетерминированного конечного автомата , то для некоторого детерминированного автомата .

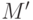Эта теорема доказывается конструктивным образом, т.е. путем указания общего алгоритма построения детерминированного автомата 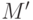, определяющего тот же язык, что и . Пусть 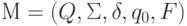; тогда мы определим 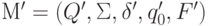следующим образом:

• совпадает с множеством состояний автомата
• 
• 
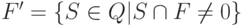
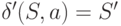• для всех 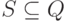, где 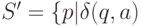содержит p для некоторого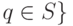

Можно показать, что 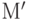задает тот же язык, что и . Таким образом, классы языков, задаваемых детерминированными и недетерминированными конечными автоматами, полностью совпадают. Естественно, детерминированные конечные автоматы удобнее, и в дальнейшем мы будем иметь дело только с ними. Следующий набросок программы демонстрирует моделирование конечного автомата (предполагается, что входная лента заканчивается символом end_of_file ):

q = q0;
c = GetChar();
while (c != eof) {
  q = move (q, c);
  c = GetChar();
}
if (q is in F) return "yes";
else return "no";

Эквивалентность конечных автоматов

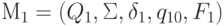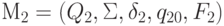Определение.Два автомата и называются эквивалентными, если они распознают один и тот же язык над алфавитом .

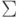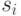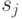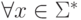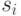Определение.Два состояния и называются эквивалентными, если верно, что . Очевидно, что если два состояния и 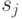эквивалентны, то 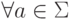состояния 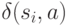и также эквивалентны

Кроме того, так как в детерминированном конечном автомате переход 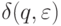может возникнуть только для конечного состояния , то никакое заключительное состояние не может быть эквивалентно незаключительному состоянию. Таким образом, если мы предположим, что начальные состояния автоматов эквивалентны, то мы можем получить и другие пары эквивалентных состояний. Если в одну из таких пар попадет заключительное состояние вместе с незаключительным, то 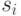и 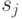неэквивалентны. Напишем алгоритм разбиения множества состояний на классы эквивалентности:

Добавить  (q10, q20) в Список;
Список = 0; /* Множество эквивалентных множеств */
for each (q in Q1+Q2) { Добавить {s} в Список; }
while (есть пара (qi, qj), входящая в Список) {
   Удалить пару (qi, qj) из Списка;
   Пусть A и A'  - такие множества, что  ;
   if (A != A') {
      A = A + A';
      for (  ) { Добавить ( 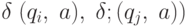   в Список; }
   }
}

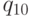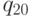Таким образом, мы получим разбиение множества на множества эквивалентных состояний, если и - эквивалентны. Теперь осталось проверить, что никакое из этих множеств не содержит заключительное и незаключительное соcтояния. Если это верно, то автоматы эквивалентны.

Минимизация конечного автомата

Учитывая, что мы можем определять эквивалентные автоматы, хотелось бы научиться находить наименьший среди них. Задача нахождения наименьшего конечного автомата, распознающего данный язык, также разрешима, причем тоже конструктивным образом. Для описания процесса нахождения наименьшего конечного автомата, введем следующее определение.

Определение. Будем говорить, что строка различает состояния и , если существует такая входная цепочка , что 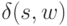является заключительным состоянием, а состояние 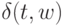не является заключительным состоянием, или, наоборот, 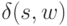не является заключительным состоянием, а состояние 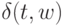является заключительным состоянием.

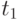Очевидно, что если некоторая строка различает состояния и 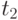такие, что 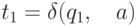и 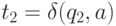, то строка aw различает состояния 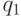и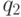

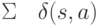Теперь перейдем к описанию процесса минимизации конечного автомата. Мы начнем с поиска и удаления всех недостижимых состояний. Затем мы должны найти такое разбиение множества состояний автомата, чтобы каждое подмножество содержало неразличимые состояния, т.е. если и принадлежат некоторому подмножеству, то для всех из и 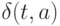также принадлежат этому подмножеству.

Для этого мы разобьем множество состояний на два подмножества: и . В дальнейшем, мы попытаемся разбить каждое из подмножеств, соблюдая указанное выше условие. Если возникает ситуация, при которой мы не можем разбить никакое множество состояний, то мы заканчиваем процесс разбиения. В результате мы получим некоторый набор множеств состояний . Каждое из 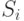содержит только неразличимые состояния. Наконец, внесем в множество состояний минимизированного автомата по одному представителю каждого из множеств 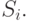На этом процесс завершается.

На следующем слайде мы приведем пример минимизации автомата.

Пример минимизации конечного автомата

Рассмотрим процесс минимизации автомата, представленного на слайде. Согласно алгоритму, вначале мы произведем удаление недостижимых состояний - в нашем примере состояние F очевидно недостижимо и потому не попадет в минимизированный автомат.

Затем мы произведем разбиение множества состояний автомата на классы эквивалентности. Укажем такую последовательность разбиений:

1. E, ABCD
2. E, ABC, D, так как .
3. E, AC, B, D, так как .

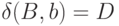Таким образом, состояния A и C неразличимы. Поэтому получаем следующий автомат: