НОУ ИНТУИТ | Основы теории вероятностей. Лекция 5: Функция распределения случайной величины. Виды распределения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 28.04.2012 | Доступ: свободный | Студентов: 3087 / 876 | Оценка: 3.86 / 2.57 | Длительность: 07:45:00

Тема: Математика

Теги: beta, анализ, биноминальное распределение, бифуркация, вычисления, графика, дискретная случайная величина, законы, несовместное событие, нормальная функция, ось ординат, полная группа, распределение пуассона, формула полной вероятности, цвета, элементарное события

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Логарифмическое нормальное распределение (логнормальное распределение)

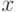Определение. Логарифмическим нормальным распределением (логнормальным распределением) называется такое распределение $u$ , которое получается из почленного логарифмирования исходного ряда $x$ , не подчиняющегося нормальному закону распределения, при условии, что среди элементов $x_{i}$ нет отрицательных и нулевых, при этом

$u_{i}=ln x_{i}.$

( 36)

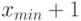В случае, если все же среди $x_{i}$ есть отрицательные или нулевые члены, то тогда можно к каждому члену ряда прибавить некоторую константу, например, $x_{min}+1$ . По одному из свойств математического ожидания, эта операция не изменит основные статистические характеристики ряда. Эта операция позволяет перейти к логнормальному распределению в указанном случае.

В результате применения операции логарифмирования (36) к исследуемому ряду су-щественно уменьшается разброс между данными. Это можно видеть из рис. 9.16 : очевидно, что 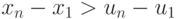$x_{n}-x_{1}>u_{n}-u_{1}$ .

Функция распределения нового ряда будет равна

$f(u)=\frac 1 {\sigma_{u} \sqrt{2\pi}} e^{-\frac {(u-M_{u})^2} {2\sigma_{u}^2}}$

( 37)

но тогда

$M_{X}=exp \left (\frac {\sigma_{u}^2+2M_{U}} 2 \right)$

( 38)

$f(x)=\frac 1 n f(u)$

( 39)

и, наконец,

$\sigma_{u}^2=e^{\sigma_{u}^{2}+2M_{U}}}\left ( e^{\sigma_{u}^2}-1\right )$

( 40)

Формулы (37) – (40) дают связь между логнормальным $U$

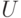и исходным $X$

распределениями.

Рис. 9.16. Геометрическая интерпретация перехода к логнормальному распределению

Закон распределения Пуассона (закон распределения редких явлений)

Все распределения при достаточно большом числе испытаний стремятся к нормальному закону распределения. Однако, если среди данных есть редкие, исключительные результаты, то распределения этих редких явлений, в то время когда основная масса стремится к нормальному закону, стремится к другому закону – закону распределения Пуассона. 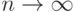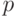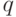Для этого закона характерно, что при $n \to \infty$ вероятности $p$ либо $q$ стремятся к нулю. В этом случае биноминальное распределение Пуассона переходит в

$P_{m}=\frac {a^me^{-a}} {m!}$

( 41)

где

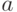имеет тот же смысл, что и в нормальном распределении.

Закон распределения Пуассона, задаваемый формулой (41), описывает вероятность появления 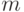$m$ событий, происходящих через приблизительно равные промежутки времени, при условии, что все события происходят независимо друг от друга и с некоторой интенсивностью, пусть даже очень маленькой, но обязательно постоянной. Число испытаний при этом велико, а вероятность появления ожидаемого события очень мала и равна 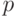$p$ . Параметр 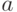$a$ тогда будет характеризовать интенсивность появления ожидаемого события в последовательности испытаний.

В таком случае попытаемся вычислить матожидание.

$M_{X}=\sum\limits_{m=0}^n m \frac {a^me^{-a}} {m!}=np$

( 42)

откуда получаем

$\sigma_{x}^2=np$

( 43)

Характерной особенностью этого вида распределения будут следующие математические соотношения:

$\mu_{3}=a; \ a=np; \ \mu_{4}=3a^2+a; \ A=\frac 1 {\sqrt a}; \ A=\frac 1 a,$

( 44)

пользуясь которыми можно без труда вычислить параметр $a$

.

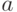Признаком распределения Пуассона служит равенство (45):

$M_{X} \approx \sigma_{x}^2$

( 45)

Пример 5. На полигоне было отобрано 150 образцов. В некоторых из них нашли присутствие редкого элемента:

Таблица возможных исходов
% содержания редкого элемента	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07
Кол-во образцов, с таким содержания редкого элемента	32	51	36	19	8	5	1	0

Определить закон распределения искомого элемента.

Решение. Для ответа на вопрос в задаче следует проверить выполнение равенства (45), являющегося характерным признаком распределения Пуассона. Для простоты вычислений будем брать не сотые доли, а числа, увеличенные в 100 раз, т.е.

$\ M_{X}=\frac {0 \cdot 32 +1 \cdot 51 +2 \cdot 36 +3 \cdot 19 +8 \cdot 4 +5 \cdot 5 + 1 \cdot 6 +0 \cdot 7} {150} \approx 1,52 ;$

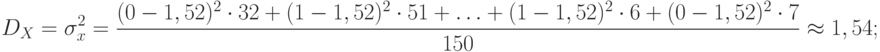
$D_{X}=\sigma_{x}^2 = \frac {(0-1,52)^2 \cdot 32 +(1-1,52)^2 \cdot 51 + \ldots + (1-1,52)^2 \cdot 6 + (0-1,52)^2 \cdot 7} {150} \approx 1,54 ;$

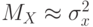В связи с тем что $M_{X} \approx \sigma_{x}^2$ , заключаем, что распределение искомого элемента подчиняется закону распределения Пуассона. Теперь, пользуясь соотношениями (42) вычислим через 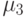$\mu_{3}$ теоретическое $a$

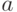, сравним его с исходной частотой 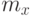$m_{x}$ , и по формуле (39) вычислим теоретическое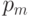 $p_{m}$

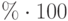$\%\cdot 100$	0	1	2	3	4	5	6	7
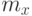$m_{x}$	32	51	36	19	8	5	1	0
$p_{x}$	0.2231	0.3346	0.251	0.1255	0.047	0.0141	0.1179	0.0008
$n \cdot p_{m}$	33.46	50.19	37.65	18.82	7.06	2.11	1.18	0.12
$a_{i}$	33	50	38	19	7	2	1	0

Как видно из последних результатов, расчетные значения 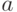$a$ почти не отличаются от реальных экспериментальных характеристик 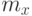$m_{x}$ , что подтверждает правильность выдвинутой гипотезы .

Дальше >>

Авторизоваться

Основы теории вероятностей

Функция распределения случайной величины. Виды распределения

Логарифмическое нормальное распределение (логнормальное распределение)

Закон распределения Пуассона (закон распределения редких явлений)

Вопросы и ответы