Комитетные методы решения задач распознавания
7.1. Теоретико-множественная постановка задачи выбора алгоритма.
Байесовский подход исходит из статистической природы наблюдений. За основу берется предположение о существовании вероятностной меры на пространстве образов, которая либо известна, либо может быть оценена. Цель состоит в разработке такого классификатора, который будет правильно определять наиболее вероятный класс для пробного образа. Тогда задача состоит в определении "наиболее вероятного" класса.
Пусть 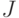 – индексное множество;
– индексное множество;  – подмножество некоторого
множества (например, множества алгоритмов);
– подмножество некоторого
множества (например, множества алгоритмов); 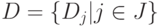 – система подмножеств.
Пусть
– система подмножеств.
Пусть  – множество, в котором необходимо найти решение. Задача
заключается в нахождении такого элемента
– множество, в котором необходимо найти решение. Задача
заключается в нахождении такого элемента  такое, что
такое, что 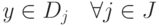 .
.
Пример. Пусть  ,
,  ,
, 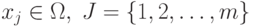 .
. 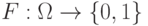 так, что
так, что 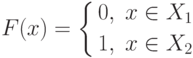 .
.
Тогда  – множество алгоритмов, дающих правильную классификацию
– множество алгоритмов, дающих правильную классификацию  :
:
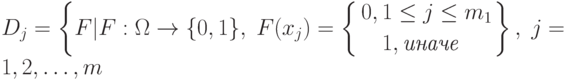
Определение. Пусть 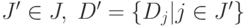 . Тогда система подмножеств
. Тогда система подмножеств 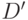 называется совместной, если
называется совместной, если  .
.
В примере условием совместности является не пересекаемость множеств 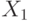 и
и 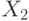 . Тогда, очевидно, что в пересечении
. Тогда, очевидно, что в пересечении 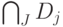 лежит
лежит 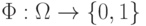 , где
, где
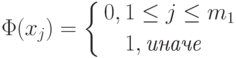
Тогда возникает вопрос: что делать, если  ? Существует два способа
решения данной проблемы:
? Существует два способа
решения данной проблемы:
Смягчить условия, описывающие  , т.е. построить
, т.е. построить  .
.
Решить задачу поиска максимальных совместных подсистем системы  ,
, 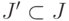
Определени е. Теоретико-множественная задача называется разрешимой в классе  ,
если
,
если 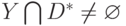 , где
, где 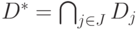 .
.
