НОУ ИНТУИТ | Криптографические методы защиты информации. Лекция 5: Необходимые сведения о случайных величинах

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 02.03.2017 | Доступ: свободный | Студентов: 2756 / 667 | Длительность: 21:50:00

Специальности: Программист, Администратор информационных систем, Специалист по безопасности, Архитектор программного обеспечения, Разработчик интернет-проектов

|

Вам нравится? Нравится 57 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

5.2.2 Пропускная способность канала и количество принятой информации

Определение 5.14 Пропускная способность канала связи - наибольшая теоретически достижимая скорость передачи информации при условии, что погрешность не превосходит заданной величины.

Определение 5.15 Скорость передачи информации - среднее количество информации, передаваемое в единицу времени. Определим выражения для расчета скорости передачи информации и пропускной способности дискретного канала связи.

При передаче каждого символа в среднем по каналу связи проходит количество информации, определяемое по формуле:

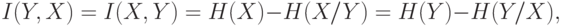I (Y, X) = I (X, Y) = H(X) - H (X/Y) = H(Y) - H (Y/X),

( 5.3)

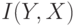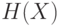где I (Y, X) - взаимная информация, т.е. количество информации, содержащееся в относительно ; H(X) - энтропия источника сообщений; 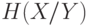H (X/Y) - условная энтропия, определяющая потерю информации на один символ, связанную с наличием помех и искажений.

При передаче сообщения 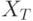X_T длительности , состоящего из элементарных символов, среднее количество передаваемой информации с учетом симметрии взаимного количества информации равно:

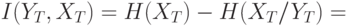( 5.4)

( 5.5)

где $T = n\bar{\tau}$ ; $\bar{\tau}$ - среднее время передачи одного символа; -число символов в сообщении длительностью .

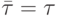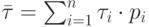Для символов равной длительности $\bar{\tau} =\tau$ , в случае неравновероятных символов неравной длительности $\bar{\tau}=\sum_{i=1}^n \tau_i\cdot p_i$ .

При этом скорость передачи информации

$C=\bar{I}(X_T,Y_T)=\lim_{T\rightarrow \infty} \frac{(X_T,Y_T)}{T} \text{ [бит/с]}.$

( 5.6)

Скорость передачи информации зависит от статистических свойств источника, метода кодирования и свойств канала.

Пропускная способность дискретного канала связи

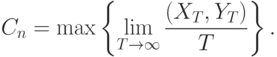$C_n= \max \left\{ \lim_{T\rightarrow \infty} \frac{(X_T,Y_T)}{T}\right\}.$

( 5.7)

Пример 5.4 [2] Источник вырабатывает 3 сообщения с вероятностям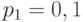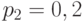и: , и 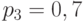. Сообщения независимы и передаются равномерным двоичным кодом () с длительностью символов, равной мс. Определить скорость передачи информации по каналу связи без помех.

Решение. Энтропия источника равна

$H=-\sum_{i=1}^{m} p_i \log_2 p_i = - \left( 0,1 \log_2 0,1 + 0,2 \log_2 0,2+ 0,7 \log_2 0,7\right)=1,16 \text{ [бит/с].}$

Для передачи 3 сообщений равномерным кодом необходимо два разряда, при этом длительность кодовой комбинации равна 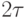$2\tau$ .

Средняя скорость передачи сигнала

$V =1/2\tau = 500 \text{ [1/c]}.$

Скорость передачи информации

$C = vH = 500\cdot1,16 = 580 \text{ [бит/с]}.$

Пример 5.5 По каналу связи передаются сообщения, вероятности которых соответственно равны:

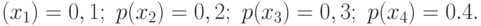
$(x_1)=0,1;\ p(x_2)=0,2;\ p(x_3)=0,3;\ p(x_4)=0.4.$

Канальная матрица, определяющая потери информации в канале связи имеет вид:

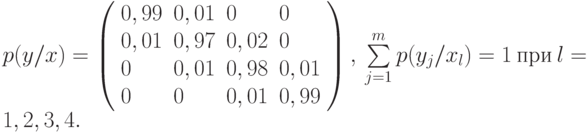
$p(y/x)=\left(\begin{array}{llll} 0,99&0,01&0&0\\ 0,01&0,97&0,02&0\\ 0&0,01&0,98&0,01\\ 0&0&0,01&0,99 \end{array} \right),\ \sum\limits_{j=1}^m p(y_j/x_l)=1 ~\text{при}~ l=1,2,3,4.$

Определить:

Энтропию источника информации - .
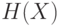Безусловную энтропию приемника информации - .
Общую условную энтропию - .
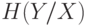Скорость передачи информации, если время передачи одного символа первичного алфавита 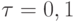$\tau = 0,1$ мс.
Определить потери информации в канале связи при передаче 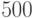символов алфавита.
Среднее количество принятой информации.
Пропускную способность канала связи.

Решение:

Энтропия источника сообщений равна
$\begin{equation} H(X)=-\sum\limits_{i=1}^{m} p(x_i) \log_2 p(x_i) = \\ - ( 0,1 \log_2 0,1+0,2 \log_2 0,2+0,3 \log_2 0,3+0,4 \log_2 0,4)= \\ 0,3322+0,4644+0,5211+0,5288=1,8465 \text{ [бит/симв.]} \end{equation}$
Вероятности появления символов на входе приемника
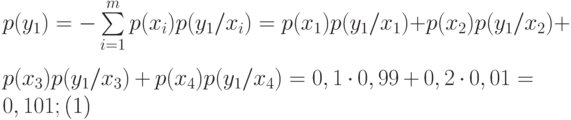
$\begin{equation} p(y_1)=-\sum\limits_{i=1}^{m} p(x_i) p(y_1 /x_i) = p(x_1)p(y_1/x_1)+p(x_2)p(y_1/x_2)+ \\ p(x_3)p(y_1/x_3)+p(x_4)p(y_1/x_4)=0,1\cdot0,99+0,2\cdot0,01=0,101; \end{equation}$

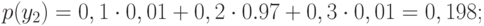
$p(y_2)=0,1\cdot0,01+0,2\cdot0.97+0,3\cdot0,01=0,198;$

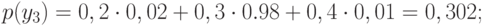$p(y_3)=0,2\cdot0,02+0,3\cdot0.98+0,4\cdot0,01=0,302;$

$p(y_4)=0,3\cdot0,01+0,4\cdot0.99=0,399.$
Проверка:
$\sum_{i=1}^m p(y_i)=-0,101+0,198+0,302+0,399=1.$
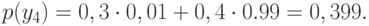Энтропия приемника информации равна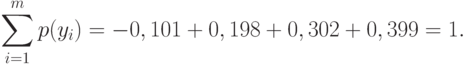
$\begin{equation} H(Y)=-\sum\limits_{i=1}^m p(y_i) \log_2 p(y_i)=\\ -(0,101 \log_2 0,101 + 0,198 \log_2 0,198 + 0,302 \log_2 0,302 + 0,399 \log_2 0,399 =\\ 0,334+0,4626+0,5216+0,5290=1,85 \text{ [бит/симв].} \end{equation}$
Общая условная энтропия равна
$H(Y/X)=-\sum_{i=1}^m \sum_{j=1}^m p(x_i) p(y_j/x_i) \log_2 p(y_j/x_i)=\\ -\left( 0,1(0,99 \log_2 0,99 + 0,01 \log_2 0,01)+\right.\\ 0,2(0,01 \log_2 0,01 + 0,97 \log_2 0,97+ 0,02 \log_2 0,02)+\\ 0,3(0,01 \log_2 0,01 + 0,98 \log_2 0,98+ 0,01 \log_2 0,01)+\\ \left. 0,4(0,01 \log_2 0,01 + 0,99 \log_2 0,99) \right)= \\ 0,008+0,044+0,048+0,032=0,133 \text{ [бит/симв].}$
Скорость передачи информации равна:
$C=V\left(H(Y)-H(Y/X)\right)=V\left(H(X)-H(X/Y)\right)=\\ (1,85-0,132)/0,0001=17,18 \text{ [Кбит/с].}$
Потери информации в канале связи при передаче 500 символов алфавита равны:
$\Delta I=kH(Y/X) = 500\cdot 0,132=66 \text{ [бит.]}$
Среднее количество принятой информации равно:
$I=k\left(H(Y)-H(Y/X)\right)=k\left(H(X)-H(X/Y)\right)=\\ 500\cdot(1,85-0,132)=859 \text{ [бит].}$
Пропускная способность канала связи
$C_n=V\left( \log_2 m - H(Y/X) \right)=(2-0,132)/0,0001=18,68 \text{ [Кбит/с].}$

Список литературы

Харин Ю.С., Берник В.И., Матвеев Г.В. Математические основы криптологии - Минск: БГУ, 1999. - 319 с.
Блинцов С.В. Сборник примеров и задач по теории информации. Николаев: НУК им. адмирала Макарова, 2004..
Рябко Б.А., Филонов А.Н. Криптографические методы защиты информации: Учебное пособие для ВУЗов. Новосиб.: СибГУТИ, 2008. - 229 с.

Дальше >>

Авторизоваться

Криптографические методы защиты информации

Необходимые сведения о случайных величинах

5.2.2 Пропускная способность канала и количество принятой информации

Список литературы

Вопросы и ответы