|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Слияние и сортировка слиянием
Абстрактное обменное слияние
Хотя реализация слияния требует дополнительной памяти, все же абстракция обменного слияния полезна при реализации изучаемых здесь методов сортировки. В нашей следующей реализации слияния это будет подчеркнуто с помощью сигнатуры функции merge (a, l, m, r), что означает, что подпрограмма merge помещает результат слияния a[1], ..., a[m] и a[m+1], ..., a[r] в объединенный упорядоченный массив a[1], ..., a[r]. Эту программу слияния можно было бы реализовать, сначала скопировав все входные данные во вспомогательный массив и затем применив базовый метод из программы 8.1, однако пока мы не будем делать этого, а сначала внесем в данный подход одно усовершенствование. И хотя выделения дополнительной памяти для вспомогательного массива, по-видимому, на практике не избежать, в разделе 8.4 мы рассмотрим дальнейшие улучшения, которые позволят избежать дополнительных затрат времени на копирование массива.
Вторая заслуживающая внимания основная характеристика базового слияния заключается в том, что внутренний цикл содержит две проверки для определения, исчерпаны ли входные массивы. Понятно, что обычно эти проверки дают отрицательный результат, и так и напрашивается использование сигнальных ключей, позволяющих отказаться от них. То есть если в конец массива a и массива aux добавить элементы с ключами, большими значений всех других ключей, эти проверки можно удалить: если массив a (b) будет исчерпан, сигнальный ключ заставляет выбирать следующие элементы и помещать их в массив c только из массива b (a), вплоть до окончания слияния.
Однако, как было показано в "Элементарные методы сортировки" и "Быстрая сортировка" , сигнальными ключами не всегда удобно пользоваться: либо потому, что не всегда легко определить наибольшее значение ключа, либо потому, что сигнальный ключ трудно вставить в массив. В случае слияния существует достаточно простое средство, которое показано на рис. 8.1.
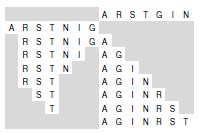
Для слияния двух упорядоченных по возрастанию файлов они копируются в другой файл, причем второй файл копируется сразу за первым в обратном порядке. Тогда можно следовать следующему простому правилу: в выходной файл выбирается левый или правый элемент - тот, у которого ключ меньше. Максимальный ключ выполняет роль сигнального для обоих файлов, где бы он ни находился. На данном рисунке показано слияние файлов A R S T и G I N.
Для слияния двух упорядоченных по возрастанию файлов они копируются в другой файл, причем второй файл копируется сразу за первым в обратном порядке. Тогда можно следовать следующему простому правилу: в выходной файл выбирается левый или правый элемент - тот, у которого ключ меньше. Максимальный ключ выполняет роль сигнального для обоих файлов, где бы он ни находился. На данном рисунке показано слияние файлов A R S T и G I N.
В основу этого метода положена следующая идея: если при реализации обменной абстракции все-таки не отказываться от копирования массивов, то при копировании второго файла можно просто изменить порядок его элементов (без дополнительных затрат) - чтобы связанный с ним индекс перемещался справа налево. При таком упорядочении наибольший элемент, в каком бы он файле не находился, служит сигнальным ключом для другого массива. Программа 8.2 является эффективной реализацией абстрактного обменного слияния, основанной на этой идее, и служит отправной точкой для разработки алгоритмов сортировки, которые рассматриваются далее в этой главе. В ней все же используется вспомогательный массив с размером, пропорциональным выходному файлу, но она более эффективна, чем примитивная реализация, поскольку в ней не нужны проверки на окончание сливаемых массивов.
Последовательность ключей, которая сначала увеличивается, а затем уменьшается (или сначала уменьшается, а затем увеличивается), называется битонической (bitonic) последовательностью. Сортировка битонической последовательности эквивалентна слиянию, но иногда удобно представить задачу слияния в виде задачи битонической сортировки; рассмотренный метод, позволяющий избежать вставки сигнальных ключей, как раз и служит простым примером этого.
Одно из важных свойств программы 8.1 заключается в том, что реализуемое ею слияние устойчиво: оно сохраняет относительный порядок элементов с одинаковыми ключами. Эту характеристику нетрудно проверить, и при реализации абстрактного обменного слияния часто имеет смысл убедиться в сохранении устойчивости, т.к., как будет показано в разделе 8.3, устойчивое слияние приводит к устойчивым методам сортировки. Свойство устойчивости не всегда просто сохранить: например, программа 8.2 не обеспечивает устойчивости (см. упражнение 8.6). Это обстоятельство еще больше усложняет проблему разработки алгоритма по-настоящему обменного слияния.
Программа 8.2. Абстрактное обменное слияние
Данная программа выполняет слияние двух файлов без использования сигнальных ключей, для чего второй массив копируется во вспомогательный массив aux в обратном порядке, сразу за концом первого массива (т.е. устанавливая в aux битонический порядок). Первый цикл for пересылает первый массив и оставляет i равным l, т.е. готовым для начала слияния. Второй цикл for пересылает второй массив, после чего j равно r. Затем в процессе слияния (третий цикл for) наибольший элемент служит сигнальным ключом независимо от того, в каком массиве он находится. Внутренний цикл этой программы достаточно короткий (пересылка в aux, сравнение, пересылка обратно в a, увеличение значения i или j на единицу, увеличение и проверка значения k).
template <class Item>
void merge(Item a[], int l, int m, int r)
{ int i, j;
static Item aux[maxN];
for (i = m+1; i > l; i—) aux[i-1] = a[i-1];
for (j = m; j < r; j++) aux[r+m-j] = a[j + 1];
for (int k = l; k <= r; k++)
if (aux[j] < aux[i])
a[k] = aux[j--];
else
a[k] = aux[i++];
}
Упражнения
 8.5. Покажите в стиле диаграммы 8.1, как программа 8.1 выполняет слияние ключей A E Q S U Y E I N O S T.
8.5. Покажите в стиле диаграммы 8.1, как программа 8.1 выполняет слияние ключей A E Q S U Y E I N O S T.
8.6. Объясните, почему программа 8.2 не является устойчивой, и разработайте устойчивую версию этой программы.
8.7. Что получится, если программу 8.2 применить к ключам E A S Y Q U E S T I O N?
8.8. Верно ли, что программа 8.2 правильно сливает входные массивы тогда и только тогда, когда они отсортированы? Обоснуйте ваш ответ или приведите контрпример.
Нисходящая сортировка слиянием
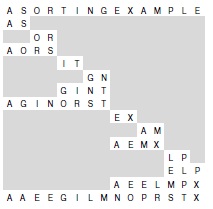
Имея в своем распоряжении процедуру слияния, нетрудно положить ее в основу рекурсивной процедуры сортировки. Чтобы отсортировать заданный файл, нужно разделить его на две части, рекурсивно отсортировать обе половины и затем слить их. Реализация этого алгоритма представлена в программе 8.3; а пример показан на рис. 8.2 рис. 8.2. Как было сказано в "Рекурсия и деревья" , этот алгоритм является одним из самых известных примеров использования принципа " разделяй и властвуй " для разработки эффективных алгоритмов.
Нисходящая сортировка слиянием аналогична принципу управления сверху вниз, при котором руководитель разбивает большую задачу на подзадачи, которые должны независимо решать его подчиненные. Если каждый руководитель будет просто разбивать свою задачу на две равные части, а потом объединять решения, полученные его подчиненными, и передавать результат своему начальству, то получится процесс, аналогичный сортировке слиянием. Работа практически не продвигается, пока не получит свою задачу кто-то, не имеющий подчиненных (в рассматриваемом случае это слияние двух файлов размером 1); но потом руководство выполняет значительную работу, объединяя результаты работы подчиненных.
Сортировка слиянием играет важную роль благодаря простоте и оптимальности заложенного в нее метода (время ее выполнения пропорционально N log N), который допускает возможность устойчивой реализации. Эти утверждения сравнительно нетрудно доказать.
Программа 8.3. Нисходящая сортировка слиянием
Эта базовая реализация сортировки слиянием является примером рекурсивной программы, основанной на принципе " разделяй и властвуй " . Для упорядочения массива a[1], ..., a[r] он разбивается на две части a[1], ..., a[m] и a[m+1], ..., a[r], которые сортируются независимо друг от друга (через рекурсивные вызовы) и вновь сливаются для получения отсортированного исходного файла. Функции merge может потребоваться вспомогательный файл, достаточно большой для помещения копии входного файла, однако эту абстрактную операцию удобно рассматривать как обменное слияние (см. текст).
template <class Item>
void mergesort(Item a[], int l, int r)
{ if (r <= l) return;
int m = (r+l)/2;
mergesort(a, l, m);
mergesort(a, m+1, r);
merge(a, l, m, r);
}
В каждой строке показан результат вызова функции merge при выполнении нисходящей сортировки слиянием. Вначале сливаются A и S, и получается A S; потом сливаются O и R, и получается O R. Затем сливаются O R и A S, и получается A O R S. После этого сливаются I T и G N, и получается G I N T, потом этот результат сливается с A O R S, и получается A G I N O R S T, и т.д. Метод рекурсивно объединяет меньшие упорядоченные файлы в большие.
Как было показано в
"Рекурсия и деревья"
(и для быстрой сортировки в
"Быстрая сортировка"
), для визуализации структуры рекурсивных вызовов рекурсивного алгоритма можно воспользоваться древовидными структурами, которые позволяют лучше понять все варианты рассматриваемого алгоритма и провести его анализ. Для сортировки слиянием структура рекурсивных вызовов зависит только от размера входного массива. Для любого заданного N определяется дерево, получившее название дерева " разделяй и властвуй " , которое описывает размер подфайлов, обрабатываемых во время выполнения программы 8.3 (см. упражнение 5.73): если N равно 1, то это дерево состоит из одного узла с меткой 1; иначе дерево состоит из корневого узла, содержащего файл размером N, поддерева, представляющего левый подфайл размером 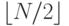 и поддерева, представляющего правый подфайл размером
и поддерева, представляющего правый подфайл размером 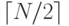 . Таким образом, каждый узел этого дерева соответствует вызову метода mergesort, а его метка показывает размер задачи, соответствующей этому рекурсивному вызову.
. Таким образом, каждый узел этого дерева соответствует вызову метода mergesort, а его метка показывает размер задачи, соответствующей этому рекурсивному вызову.
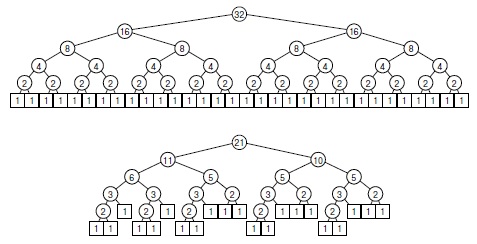
Если N равно степени 2, это построение дает полностью сбалансированное дерево со степенями 2 во всех узлах и единицами во всех внешних узлах. Если N не является степенью 2, вид дерева усложняется. На рис. 8.3 рис. 8.3 представлены примеры обоих случаев. Ранее мы уже сталкивались с такими деревьями - при изучении в "Рекурсия и деревья" алгоритма с такой же структурой рекурсивных вызовов, как и у сортировки слиянием.
Структурные свойства деревьев " разделяй и властвуй " имеют непосредственное отношение к анализу сортировки слиянием. Например, общее количество сравнений, выполняемых алгоритмом, в точности равно сумме всех меток узлов.
Лемма 8.1. Для сортировки любого файла из N элементов сортировка слиянием выполняет порядка NlgN сравнений.
В реализациях, описанных в разделах 8.1 и 8.2, для каждого слияния двух под-массивов размером N/2 нужно N сравнений (это значение может отличаться 1 или 2, в зависимости от способа использования сигнальных ключей). Следовательно, общее количество сравнений для всей сортировки может быть описано стандартным рекуррентным соотношением вида " разделяй и властвуй " : 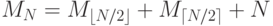 , при
M1 = 0
. Это рекуррентное соотношение описывает также сумму меток узлов и длину внешнего пути дерева " разделяй и властвуй " с N узлами (см. упражнение 5.73). Данное утверждение нетрудно проверить, когда N является степенью числа 2 (см. формулу 2.4), и доказать методом индукции для произвольного N. Непосредственное доказательство содержится в упражнениях 8.12-8.14.
, при
M1 = 0
. Это рекуррентное соотношение описывает также сумму меток узлов и длину внешнего пути дерева " разделяй и властвуй " с N узлами (см. упражнение 5.73). Данное утверждение нетрудно проверить, когда N является степенью числа 2 (см. формулу 2.4), и доказать методом индукции для произвольного N. Непосредственное доказательство содержится в упражнениях 8.12-8.14. 
На этих диаграммах показаны размеры подзадач, создаваемых нисходящей сортировкой слиянием. В отличие от, скажем, деревьев, соответствующих быстрой сортировке, эти структуры зависят только от размера первоначального файла и не зависят от значений ключей. На верхней диаграмме показана сортировка файла из 32 элементов. Сначала выполняется (рекурсивное) упорядочение двух файлов из 16 элементов, а затем их слияние. Файлы из 16 элементов сортируются (рекурсивно) с помощью (рекурсивной) сортировки файлов из 8 элементов и т.д. Для файлов, размер которых не равен степени двух, получается более сложная структура, пример которой приведен на нижней диаграмме.
Лемма 8.2. Сортировке слиянием нужен объем дополнительной памяти, пропорциональный N.
Это факт очевиден из обсуждения в разделе 8.2. Можно кое-что сделать для уменьшения размера дополнительной памяти - за счет существенного усложнения алгоритма (см., например, упражнение 8.21). Как будет показано в разделе 8.7, сортировка слиянием эффективна и в том случае, если сортируемый файл организован в виде связного списка. В этом случае данное свойство выполняется, но нужна дополнительная память для ссылок. В случае массивов, как было сказано в разделе 8.2 и будет сказано в разделе 8.4, можно выполнять слияние на месте (обсуждение этой темы будет продолжено в разделе 8.4), однако эта стратегия вряд ли применима на практике. 
Лемма 8.3. Сортировка слиянием устойчива, если устойчив используемый при этом метод слияния.
Это утверждение легко проверить методом индукции. Для реализации метода слияния, наподобие предложенного в программе 8.1, легко показать, что относительное расположение повторяющихся ключей не нарушается. Однако, чем сложнее алгоритм, тем выше вероятность того, что эта устойчивость будет нарушена (см. упражнение 8.6). 
Лемма 8.4. Требования к ресурсам сортировки слиянием не зависят от исходной упорядоченности входных данных.
В наших реализациях от входных данных зависит только порядок, в котором элементы обрабатываются во время слияний. Каждый проход требует памяти и числа шагов, пропорциональных размеру подфайла, из-за пересылки данных во вспомогательный массив. Две ветви оператора if из-за особенностей компиляции могут выполняться за слегка различное время, что может привести к некоторой зависимости времени выполнения от характера входных данных, однако число сравнений и других операций над входными данными не зависит от того, как упорядочен входной файл. Обратите внимание на то, что это отнюдь не эквивалентно утверждению, что алгоритм не адаптивный (см.
"Элементарные методы сортировки"
) - ведь последовательность сравнений зависит от упорядоченности входных данных. 
Упражнения
8.9. Приведите последовательность слияний, выполняемых программой 8.3 при сортировке ключей E A S Y Q U E S T I O N.
8.10. Начертите деревья " разделяй и властвуй " для N = 16, 24, 31, 32, 33 и 39.
8.11. Реализуйте рекурсивную сортировку слиянием для массивов, используя идею трехпутевого, а не двухпутевого слияния.
8.12. Докажите, что все узлы с метками 1 в деревьях " разделяй и властвуй " расположены на двух нижних уровнях.
8.13. Докажите, что метки в узлах на каждом уровне сбалансированного дерева размером N в сумме дают N, за исключением, возможно, нижнего уровня.
8.14. Используя упражнения 8.12 и 8.13, докажите, что количество сравнений, необходимых для выполнения сортировки слиянием, находится в пределах между NlgN и N lgN + N.
8.15. Найдите и докажите зависимость между количеством сравнений, используемых сортировкой слиянием, и количеством битов в  -разрядных положительных числах, меньших N.
-разрядных положительных числах, меньших N.