Полнота исчисления предикатов
Полнота исчисления предикатов
В этом разделе мы докажем, что всякая общезначимая формула выводима в исчислении предикатов. Мы будем следовать схеме, использованной в разделе "Второе доказательство теоремы о полноте", и введем понятия непротиворечивой и полной теории.
Фиксируем некоторую сигнатуру  . Пусть
. Пусть  — теория в сигнатуре
— теория в сигнатуре  , то есть произвольное
множество замкнутых формул этой сигнатуры.
Говорят, что теория
, то есть произвольное
множество замкнутых формул этой сигнатуры.
Говорят, что теория  противоречива,
если в ней выводится некоторая формула
противоречива,
если в ней выводится некоторая формула  и ее отрицание
и ее отрицание  . В этом случае из
. В этом случае из  выводится любая формула, так как имеется
аксиома
выводится любая формула, так как имеется
аксиома 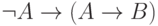 . Если теория
. Если теория  не
является противоречивой, то она называется
непротиворечивой.
не
является противоречивой, то она называется
непротиворечивой.
99. Докажите, что теория противоречива тогда и только тогда, когда в
ней выводится формула 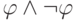 (здесь
(здесь  — произвольная формула сигнатуры).
— произвольная формула сигнатуры).
Непосредственно из определения следует, что всякое подмножество непротиворечивого множества непротиворечиво. Кроме того, если бесконечное множество противоречиво, то некоторое его конечное подмножество тоже противоречиво (поскольку в выводе участвует лишь конечное число формул).
Синтаксическое понятие непротиворечивости мы будем сравнивать с
семантическим понятием совместности. Пусть имеется некоторая
интерпретация  сигнатуры
сигнатуры  . Напомним, что она
называется моделью теории
. Напомним, что она
называется моделью теории  , если все формулы из
, если все формулы из  истинны
в
истинны
в  . Множество
. Множество  называется совместным,
если оно имеет модель, то есть если все его формулы истинны в
некоторой интерпретации.
называется совместным,
если оно имеет модель, то есть если все его формулы истинны в
некоторой интерпретации.
Теорема 45 (о корректности; переформулировка). Любое совместное множество замкнутых формул непротиворечиво.
Пусть все формулы из  истинны в некоторой
интерпретации
истинны в некоторой
интерпретации  . Может ли оказаться, что
. Может ли оказаться, что  и
и 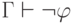 для некоторой
замкнутой формулы
для некоторой
замкнутой формулы  ? Легко понять, что нет. В самом деле, в этом
случае теорема 44 показывает, что формулы
? Легко понять, что нет. В самом деле, в этом
случае теорема 44 показывает, что формулы  и
и  должны быть
одновременно истинны в
должны быть
одновременно истинны в  , что, очевидно, невозможно.
, что, очевидно, невозможно.
Для доказательства обратного утверждения (о совместности непротиворечивой теории) нам понадобится понятие полной теории.
Непротиворечивое множество  , состоящее из замкнутых
формул сигнатуры
, состоящее из замкнутых
формул сигнатуры  , называется полным в этой
сигнатуре, если для любой замкнутой формулы
, называется полным в этой
сигнатуре, если для любой замкнутой формулы  этой сигнатуры либо
формула
этой сигнатуры либо
формула  , либо ее отрицание
, либо ее отрицание 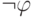 выводятся из
выводятся из  .
.
Другими словами, теория полна, если из любых двух формул  и
и  (соответствующей сигнатуры)
ровно одна является теоремой этой теории.
(соответствующей сигнатуры)
ровно одна является теоремой этой теории.
Полное множество можно получить, взяв какую-либо интерпретацию и рассмотрев все замкутые формулы, истинные в этой интерпретации. (Впоследствии мы увидим, что любое полное множество может быть получено таким способом — это легко следует из теоремы 46.)
В определении полноты существенно, что мы ограничиваемся замкнутыми
формулами той же сигнатуры. Например, если мы возьмем
одноместный предикатный символ  , не входящий в
, не входящий в  , то формулы из
, то формулы из  про него ничего не утверждают, и потому,
скажем, ни формула
про него ничего не утверждают, и потому,
скажем, ни формула  , ни ее отрицание не
выводимы из
, ни ее отрицание не
выводимы из  . Замкнутость формулы
. Замкнутость формулы  тоже
важна. Например, множество всех истинных в натуральном ряду формул
сигнатуры
тоже
важна. Например, множество всех истинных в натуральном ряду формул
сигнатуры 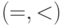 полно, но ни формула
полно, но ни формула 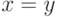 , ни
формула
, ни
формула  из него не выводятся, иначе по правилу обобщения мы
получили бы ложную в
из него не выводятся, иначе по правилу обобщения мы
получили бы ложную в 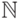 формулу
формулу  или
или 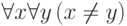 .
.
Полное множество подобно мировоззрению
человека, достигшего предела умственного развития: на все, что
входит в круг его понятий (выражается формулой сигнатуры  ), он имеет точку зрения. Но это не относится ни к
формулам большей сигнатуры (содержащим новые для него понятия),
ни к формулам с параметрами (поскольку значения параметров не
фиксированы).
), он имеет точку зрения. Но это не относится ни к
формулам большей сигнатуры (содержащим новые для него понятия),
ни к формулам с параметрами (поскольку значения параметров не
фиксированы).
Теперь мы готовы к доказательству основного результата этого раздела.
Теорема 46 (полнота исчисления предикатов, сильная форма). Любая непротиворечивая теория совместна.
Напомним, как мы доказывали аналогичное утверждение для
высказываний. Мы расширяли наше непротиворечивое
множество  до полного
множества
до полного
множества  , а потом полагали
пропозициональную переменную
, а потом полагали
пропозициональную переменную  истинной, если
истинной, если 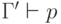 . Здесь этого будет недостаточно, как мы увидим (например,
непонятно, откуда брать носитель искомой модели). Но начало
рассуждения будет таким же.
. Здесь этого будет недостаточно, как мы увидим (например,
непонятно, откуда брать носитель искомой модели). Но начало
рассуждения будет таким же.
Лемма 1. Для всякого непротиворечивого
множества  замкнутых формул сигнатуры
замкнутых формул сигнатуры  существует полное непротиворечивое множество
существует полное непротиворечивое множество  замкнутых формул той же
сигнатуры, содержащее
замкнутых формул той же
сигнатуры, содержащее  .
.
Доказательство повторяет рассуждение
раздела "Второе доказательство теоремы о полноте":
рассматривая по очереди замкнутые формулы, мы добавляем либо их, либо их
отрицания в множество  .
.
Это можно сделать без труда для конечной или счетной сигнатуры (тогда множество всех замкнутых формул этой сигнатуры счетно); для общего случая надо воспользоваться трансфинитной индукцией или леммой Цорна, как объяснялось в разделе "Второе доказательство теоремы о полноте". Лемма 1 доказана.
Как же нам теперь построить модель полного множества  ?
Прежде всего надо решить, что будет носителем этой модели.
Заметим, что в сигнатуре могут быть некоторые константы
(функциональные символы валентности
?
Прежде всего надо решить, что будет носителем этой модели.
Заметим, что в сигнатуре могут быть некоторые константы
(функциональные символы валентности  ). Им должны
соответствовать некоторые элементы носителя. Кроме того,
замкнутым термам (которые не содержат никаких переменных, только
константы) также должны соответствовать элементы носителя.
Попробуем взять в качестве носителя как раз множество
). Им должны
соответствовать некоторые элементы носителя. Кроме того,
замкнутым термам (которые не содержат никаких переменных, только
константы) также должны соответствовать элементы носителя.
Попробуем взять в качестве носителя как раз множество  всех
замкнутых термов нашей сигнатуры. При этом понятно, как надо
определять сигнатурные функции на этом множестве: функция,
соответствующая символу
всех
замкнутых термов нашей сигнатуры. При этом понятно, как надо
определять сигнатурные функции на этом множестве: функция,
соответствующая символу  валентности
валентности  , отображает
замкнутые термы
, отображает
замкнутые термы 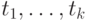 в терм
в терм 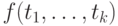 . (Это определение никак не зависит от
. (Это определение никак не зависит от  .)
.)
Предикаты на этом множестве определяем так: если  —
предикатный символ, а
—
предикатный символ, а 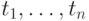 — замкнутые термы, то
предикат, соответствующий символу
— замкнутые термы, то
предикат, соответствующий символу  , истинен на термах
, истинен на термах 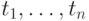 , если формула
, если формула 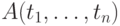 выводима из
выводима из  .
.
Тем самым интерпретация полностью описана, и мы хотели бы
доказать, что все формулы из  в ней истинны. Мы будем
доказывать по индукции такой факт:
если
в ней истинны. Мы будем
доказывать по индукции такой факт:
если  , то формула
, то формула  истинна в построенной интерпретации, а если
истинна в построенной интерпретации, а если 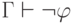 ,
то формула
,
то формула  ложна.
ложна.
Однако без дополнительных предположений о множестве  этот план обречен на неудачу, поскольку замкнутых термов может
быть совсем мало (или даже вовсе не быть), в то время как
соответствующая теория не имеет конечных моделей. Если начать
индуктивное рассуждение, то выяснится, что трудность возникает в
случае, когда формула
этот план обречен на неудачу, поскольку замкнутых термов может
быть совсем мало (или даже вовсе не быть), в то время как
соответствующая теория не имеет конечных моделей. Если начать
индуктивное рассуждение, то выяснится, что трудность возникает в
случае, когда формула  начинается с квантора. Например,
может оказаться, что формула
начинается с квантора. Например,
может оказаться, что формула 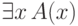 выводима из
множества
выводима из
множества  , в то время как ни для какого замкнутого
терма
, в то время как ни для какого замкнутого
терма  формула
формула 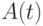 не выводима из
не выводима из  . Тогда формула
. Тогда формула 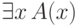 будет ложной в описанной нами модели (хотя
выводимой). Чтобы преодолеть эту трудность, мы наложим
дополнительные требования на множество
будет ложной в описанной нами модели (хотя
выводимой). Чтобы преодолеть эту трудность, мы наложим
дополнительные требования на множество  .
.
Назовем теорию (множество замкнутых формул сигнатуры  )
экзистенциально полной в сигнатуре
)
экзистенциально полной в сигнатуре  ,
если для всякой замкнутой формулы
,
если для всякой замкнутой формулы 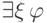 сигнатуры
сигнатуры  , выводимой из
, выводимой из  , найдется замкнутый терм
, найдется замкнутый терм  этой сигнатуры, для которого
этой сигнатуры, для которого 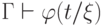 .
.
Если множество  полно и экзистенциально полно, то
описанная выше конструкция с замкнутыми термами дает его модель.
Прежде чем проверять это, покажем, как расширить
полно и экзистенциально полно, то
описанная выше конструкция с замкнутыми термами дает его модель.
Прежде чем проверять это, покажем, как расширить  до
полного и экзистенциально полного множества. Ключевую роль здесь
играет такая лемма:
до
полного и экзистенциально полного множества. Ключевую роль здесь
играет такая лемма:
