Исчисление высказываний
23. Докажите, что формула 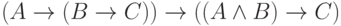 , так же как и обратная к ней формула (в которой
посылка и заключение переставлены), являются теоремами
исчисления высказываний. Докажите аналогичное утверждение про
формулы
, так же как и обратная к ней формула (в которой
посылка и заключение переставлены), являются теоремами
исчисления высказываний. Докажите аналогичное утверждение про
формулы  и
и 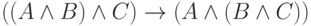 .
.
Аксиомы 6-7 позволяют утверждать, что 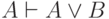 и
и 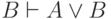 . Аксиома 8 обеспечивает такое правило:
. Аксиома 8 обеспечивает такое правило:
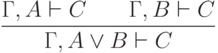
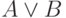 . Разберем два случая. Если выполнено
. Разберем два случая. Если выполнено  , то
, то  и потому
и потому  . Если выполнено
. Если выполнено  ,
то
,
то  и потому
и потому  . В обоих случаях верно
. В обоих случаях верно  .
Значит,
.
Значит, 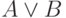 влечет
влечет  ."
."Обоснование: дважды воспользуемся
леммой о дедукции, получив 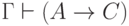 и
и 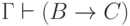 , а затем дважды применим правило MP
к этим формулам и аксиоме
, а затем дважды применим правило MP
к этим формулам и аксиоме 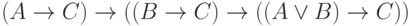 .
Получив формулу
.
Получив формулу  , опять применим правило MP
к ней и формуле
, опять применим правило MP
к ней и формуле 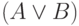 .
.
24. Докажите, что следующие формулы, а также обратные к ним (меняем местами посылку и заключение) являются теоремами исчисления высказываний:

У нас остались еще три аксиомы, касающиеся
отрицания. Аксиома 9 гарантирует, что из противоречивого набора
посылок можно вывести что угодно: если 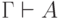 и
и 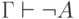 , то
, то 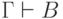 для любого
для любого  . Аксиома 10, напротив, объясняет, как можно вывести отрицание
некоторой формулы
. Аксиома 10, напротив, объясняет, как можно вывести отрицание
некоторой формулы  : надо допустить
: надо допустить  и вывести два противоположных
заключения
и вывести два противоположных
заключения  и
и 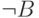 . Точнее говоря, имеет место такое
правило:
. Точнее говоря, имеет место такое
правило:

Аксиомы 9 и 10 позволяют вывести некоторые логические законы,
связанные с отрицанием. Докажем, например, что (для любых формул  и
и  ) формула
) формула
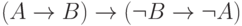
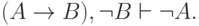
 какую-либо формулу и ее отрицание (в данном случае
формулы
какую-либо формулу и ее отрицание (в данном случае
формулы  и
и 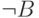 ).
).25. Выведите формулы 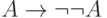 и
и 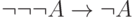 с помощью аналогичных рассуждений.
с помощью аналогичных рассуждений.
Последняя аксиома, называемая "законом исключенного третьего", и иногда читаемая как "третьего не дано" (tertium non datur в латинском оригинале), вызвала в первой половине века большое количество споров. (См. раздел об интуиционистской логике,в которой этой аксиомы нет.)
Из нее можно вывести закон "снятия двойного отрицания",
имеющий вид 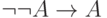 . В самом деле, достаточно
показать, что
. В самом деле, достаточно
показать, что 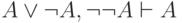 . По правилу
разбора случаев, достаточно установить, что
. По правилу
разбора случаев, достаточно установить, что  (это очевидно) и что
(это очевидно) и что  (а это верно, так как из двух противоречащих друг другу
формул выводится что угодно с помощью аксиомы 8).
(а это верно, так как из двух противоречащих друг другу
формул выводится что угодно с помощью аксиомы 8).
26. Докажите, что формула 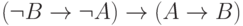 является
теоремой исчисления высказываний. (Указание: используйте закон исключенного третьего.)
является
теоремой исчисления высказываний. (Указание: используйте закон исключенного третьего.)
27. Исключим из числа аксиом исчисления высказываний закон исключенного третьего, заменив его на закон снятия двойного отрицания. Покажите, что от этого класс выводимых формул не изменится.
28. Докажите, что при наличии аксиомы исключенного третьего (11) аксиома (10) является лишней — ее (точнее следовало бы сказать: любой частный случай этой схемы аксиом) можно вывести из остальных аксиом.
Теперь уже можно доказать теорему о полноте: всякая тавтология
выводима в исчислении высказываний. Идея доказательства состоит
в разборе случаев. Поясним ее на примере. Пусть  —
произвольная формула, содержащая переменные
—
произвольная формула, содержащая переменные 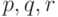 .
Предположим, что
.
Предположим, что  истинна, когда все три переменные истинны.
Тогда, как мы докажем,
истинна, когда все три переменные истинны.
Тогда, как мы докажем,
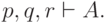
 соответствует утверждение о выводимости. Например, если
соответствует утверждение о выводимости. Например, если  ложна, когда
ложна, когда  и
и  ложны, а
ложны, а  истинно,
то
истинно,
то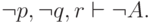
 является тавтологией, то окажется, что она
выводима из всех восьми возможных вариантов посылок. Пользуясь
законом исключенного третьего, можно постепенно избавляться от
посылок. Например, из
является тавтологией, то окажется, что она
выводима из всех восьми возможных вариантов посылок. Пользуясь
законом исключенного третьего, можно постепенно избавляться от
посылок. Например, из 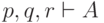 и
и  можно получить
можно получить  , то есть
, то есть 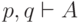 (поскольку
(поскольку  является аксиомой).
является аксиомой).Проведем это рассуждение подробно. Для начала докажем такую лемму:
Лемма 3. Для произвольных формул  и
и 
![\begin{align*}
P,Q&\vdash (P\land Q);& P,Q&\vdash (P\lor Q);\\
P,\lnot Q&\vdash \lnot (P\land Q);& P,\lnot Q&\vdash (P\lor Q);\\
\lnot P,Q&\vdash \lnot (P\land Q);& \lnot P,Q&\vdash (P\lor Q);\\
\lnot P, \lnot Q;&\vdash \lnot (P\land Q)& \lnot P,
\lnot Q&\vdash \lnot (P\lor Q);\\[1.5ex]
P,Q&\vdash (P\to Q);&&\\
P,\lnot Q&\vdash \lnot (P\to Q);& P&\vdash \lnot (\lnot P);\\
\lnot P,Q&\vdash (P\to Q);& \lnot P&\vdash \lnot P.\\
\lnot P, \lnot Q&\vdash (P\to Q);&&
\end{align*}](/sites/default/files/tex_cache/96ace2d7cacb3ac1d628721244161c23.png)
Эта лемма говорит, что если принять в качестве гипотез
истинность или ложность формул  и
и  , являющихся
частями конъюнкции, дизъюнкции или импликации, то можно будет доказать
или опровергнуть всю формулу (в зависимости от того, истинна она
или ложна). Последняя часть содержит аналогичное утверждение про отрицание.
, являющихся
частями конъюнкции, дизъюнкции или импликации, то можно будет доказать
или опровергнуть всю формулу (в зависимости от того, истинна она
или ложна). Последняя часть содержит аналогичное утверждение про отрицание.
После предпринятой нами тренировки доказать эти утверждения
несложно. Например, убедимся, что 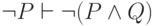 .
Для этого достаточно вывести два противоположных
утверждения из
.
Для этого достаточно вывести два противоположных
утверждения из 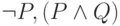 — ими будут утверждения
— ими будут утверждения  и
и 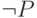 .
.
Проверим еще одно утверждение:  . Нам надо вывести два противоположных утверждения из
. Нам надо вывести два противоположных утверждения из 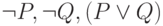 . Покажем, что из
. Покажем, что из 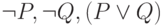 следует все, что угодно. По правилу разбора
случаев достаточно убедиться, что из
следует все, что угодно. По правилу разбора
случаев достаточно убедиться, что из 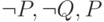 и из
и из  следует все, что угодно — но это мы знаем.
следует все, что угодно — но это мы знаем.
Утверждения, касающиеся импликации, просты: в самом деле, мы
знаем, что 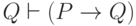 благодаря аксиоме 1, а
благодаря аксиоме 1, а 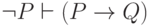 благодаря аксиоме 9.
благодаря аксиоме 9.
Остальные утверждения леммы столь же просты.
Теперь мы можем сформулировать утверждение о разборе случаев для произвольной формулы.
Лемма 4. Пусть  — произвольная формула, составленная
из переменных
— произвольная формула, составленная
из переменных 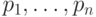 . Тогда для каждой строки таблицы
истинности формулы
. Тогда для каждой строки таблицы
истинности формулы  имеет место соответствующее утверждение о
выводимости: если
имеет место соответствующее утверждение о
выводимости: если  , и значение формулы
, и значение формулы  есть
есть  при
при 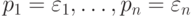 ,
то
,
то

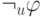 обозначает
обозначает  при
при 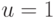 и
и 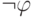 при
при 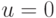 (напомним, что
(напомним, что  обозначает истину, а
обозначает истину, а  — ложь).
— ложь).Лемма очевидно доказывается индукцией по построению формулы  .
Мы имеем посылки, утверждающие истинность или ложность
переменных, и для всех подформул (начиная с переменных и идя ко
всей формуле) выводим их или их отрицания с помощью леммы 3.
.
Мы имеем посылки, утверждающие истинность или ложность
переменных, и для всех подформул (начиная с переменных и идя ко
всей формуле) выводим их или их отрицания с помощью леммы 3.
Если формула  является тавтологией, то из всех
является тавтологией, то из всех 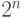 вариантов посылок выводится именно она, а не ее отрицание.
Тогда правило разбора случаев и закон исключенного третьего
позволяют избавиться от посылок: сгруппируем их в пары,
отличающиеся в позиции
вариантов посылок выводится именно она, а не ее отрицание.
Тогда правило разбора случаев и закон исключенного третьего
позволяют избавиться от посылок: сгруппируем их в пары,
отличающиеся в позиции 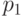 (в одном наборе посылок стоит
(в одном наборе посылок стоит 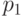 , в другом
, в другом 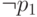 ), по правилу разбора случаев
заменим их на посылку
), по правилу разбора случаев
заменим их на посылку  , которую можно выбросить (она
является аксиомой). Сделав так для всех пар, получим
, которую можно выбросить (она
является аксиомой). Сделав так для всех пар, получим 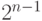 выводов, в посылках которых нет
выводов, в посылках которых нет 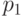 ;
повторим этот процесс с посылками
;
повторим этот процесс с посылками 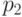 ,
, 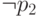 и т. д. В конце концов мы убедимся, что формула
и т. д. В конце концов мы убедимся, что формула  выводима без посылок, как и утверждает теорема о полноте.
выводима без посылок, как и утверждает теорема о полноте.
