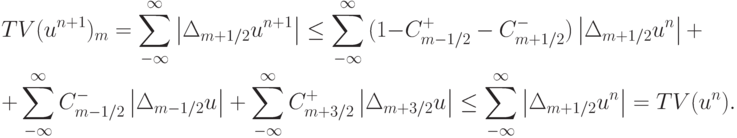НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1275 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

5.4. Метод коррекции потоков Бориса - Бука

Метод коррекции потоков предложен в [15.12], как схема "предиктор - корректор". На этапе "предиктор" погрешность метода вносит в численное решение поток численной диффузии (вязкости), на этапе "корректор" водятся потоки искусственной антидиффузии, уменьшающие их. Пусть 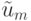$\tilde{u}_m$ — численное решение, полученное после предиктора. Корректор представляется в виде

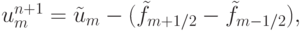
$u_m^{n + 1} = \tilde{u}_m - (\tilde{f}_{m + 1/2} - \tilde{f}_{m - 1/2} ),$

где определены антидиффузионные потоки 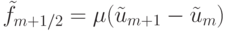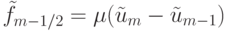$\tilde{f}_{m + 1/2} = {\mu}(\tilde{u}_{m + 1} - \tilde{u}_m)$ , $\tilde{f}_{m - 1/2} = {\mu}(\tilde{u}_m - \tilde{u}_{m - 1})$ через границы 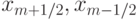$x_{m + 1/2}, x_{m - 1/2}$ , ( $\mu$ — коэффициент антидиффузии ).

В [15.13] предложен общий вид корректора:

$u_m^{n + 1} = \tilde{u}_m + {\mu}(u_{m + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n} ) + \tilde{\mu} (\tilde{u}_{m + 1} - 2 \tilde{u}_m + \tilde{u}_{m - 1} ),$

причем коэффициенты антидиффузии вычисляются с помощью подхода, предложенного в [15.6], [15.10].

5.5. TVD - схемы

Идею схем TVD (Total Variation Diminition), т.е. схем с уменьшением полной вариации, представим на примере схемы Лакса - Вендроффа [15.14]:

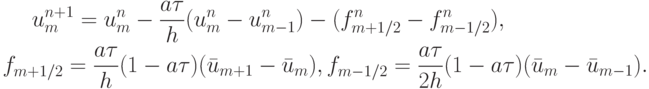
$\begin{gather*} u_m^{n + 1} = u_m^{n} - \frac{{a{\tau}}}{h}(u_m^{n} - u_{m - 1}^{n} ) - (f_{m + 1/2}^{n} - f_{m - 1/2}^{n}), \\ f_{m + 1/2} = \frac{{a{\tau}}}{h}(1 - a{\tau})(\bar{u}_{m + 1} - \bar{u}_m ), f_{m - 1/2} = \frac{{a{\tau}}}{2h}(1 - a{\tau})(\bar{u}_m - \bar{u}_{m - 1} ) . \end{gather*}$

Эта схема немонотонная, но в отсутствии последнего слагаемого $(f_{m + 1/2}^{n} - f_{m - 1/2}^{n})$ она была бы монотонной. Этот факт можно проинтерпретировать следующим образом: антидиффузионные потоки в схеме Лакса - Вендроффа слишком велики и приводят к появлению осцилляций. Следовательно, эти потоки необходимо ограничить, например, как

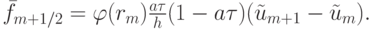
$\bar{f}_{m + 1/2} = {\varphi}(r_m ) \frac{{a{\tau}}}{h}(1 - a{\tau})(\tilde{u}_{m + 1} - \tilde{u}_m ).$

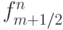Поток $f_{m + 1/2}^{n}$ ограничивается некой функцией 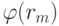${\varphi}(r_m )$ , называемой ограничителем или лимитером. Параметр r_m вычисляется по формуле

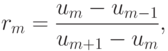
$r_m = \frac{{u_m - u_{m - 1}}}{{u_{m + 1} - u_m }},$

его можно назвать показателем гладкости решения.

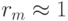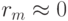Для гладких решений $r_{m} \approx 1$ , при больших же градиентах $r_{m} \approx 0$ .

Функция 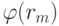${\varphi}(r_m )$ выбирается так, чтобы схема относилась к классу TVD, т.е. чтобы уменьшалась полная вариация на следующем слое по времени, 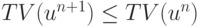$TV(u^{n + 1}) \le TV(u^n)$ . Выражение для полной вариации есть 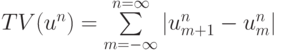$TV(u^n) = \sum\limits_{m = - \infty }^{n = \infty }{\left| {u_{m + 1}^{n} - u_m^{n}}\right|}$ . Это условие более слабое, чем условие монотонности разностной схемы.

Для того чтобы полная вариация уменьшалась, достаточно выбрать лимитер следующим образом:

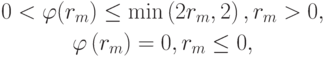
$\begin{gather*} 0 < {\varphi}(r_m ) \le \min\left({2r_m , 2}\right), r_m > 0, \\ {\varphi}\left({r_m }\right) = 0, r_m \le 0, \end{gather*}$

причем для обеспечения второго порядка аппроксимации необходимо, чтобы 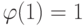${\varphi}(1) = 1$ .

Другой ограничитель имеет вид

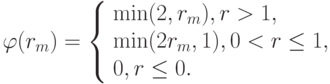
${\varphi}(r_m ) = \left\{ \begin{array}{l} {\min (2, r_m ), r > 1, } \\ {\min (2r_m , 1), 0 < r \le 1, } \\ {0, r \le 0.} \\ \end{array} \right.$

Заметим, что вместо свободных параметров в этой схеме вводится функция - ограничитель, а сама схема является одношаговой. Иногда в расчетах полагают

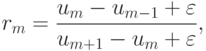
$r_m = \frac{{u_m - u_{m - 1} + \varepsilon }}{{u_{m + 1} - u_m + \varepsilon }},$

где малая величина 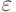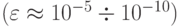$\varepsilon$ $(\varepsilon \approx 10^{ - 5} \div 10^{ - 10})$ играет роль шумового фильтра.

Вместо условия уменьшения полной вариации разностной схемы можно ввести более слабое ограничивающее условие 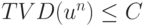$TVD(u^n) \le C$ , причем $n{\tau}\le C$ (схемы TVB).

В [15.15], [15.16] разностную схему для численного решения уравнения переноса предложено представить в виде

$u_m^{n + 1} = u_m^{n} - \frac{{a{\tau}}}{h}(u_m^{n} - u_{m - 1}^{n} ) + \frac{{a{\tau}}}{h}[{\xi_{m + 1/2} (u_{m + 1}^{n} - u_m^{n} ) - \xi_{m - 1/2} (u_m^{n} - u_{m - 1}^{n} )} ],$

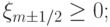где $\xi_{m \pm 1/2} \ge 0;$ или

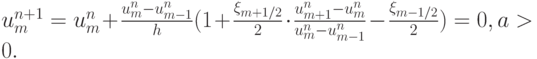
$u_m^{n + 1} = u_m^{n} + \frac{u_m^{n} - u_{m - 1}^{n}}{h}(1 + \frac{\xi_{m + 1/2}}{2} \cdot \frac{u_{m + 1}^{n} - u_m^{n}}{u_m^{n} - u_{m - 1}^{n}} - \frac{\xi_{m - 1/2}}{2}) = 0, a > 0.$

В соответствии с [15.16], эта схема будет монотонной, если выражение в скобках неотрицательно. Монотонность схемы может быть достигнута выбором коэффициента $\xi _{m \pm 1/2}$ , как функции от 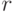. Как и ранее,

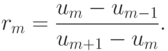
$r_m = \frac{u_m - u_{m - 1}}{u_{m + 1} - u_m }.$

Выбор весового множителя осуществим в соответствии с правилом

$\xi (r_m) = \left\{ \begin{array}{cc} {0, & r_m \le 0}, \\ {\frac{[c + b (1 - \delta)]}{(c + b)(1 - \delta)}r_m, & 0 < r_m < 1 - {\Delta}}, \\ {\frac{c + br_m}{c + b}, & |r_m - 1| \le \delta}, \\ {\frac{(c + b (1 - \delta)) - 2c \delta}{(c + b)(1 - \delta)}r_m}, & 1 + {\Delta}< r_{m < 2}, \\ {\le 2, & r_m \ge 2}. \\ \end{array} \right.$

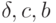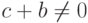Здесь $\delta, c, b$ — константы, $0 < \Delta < 1;$ если $c + b \ne 0$ получаем схему второго порядка аппроксимации, причем, при c = 1/3 и b = 2/3 — третьего порядка везде, кроме точек разрыва функций.

Отметим, что, по - видимому, основные идеи, использованные при построении TVD и ENO схем, впервые были описаны В.П.Колганом в [15.17] и Р.П.Федоренко [15.5]. Схема с различными шаблонами, которую можно рассматривать как развитие идеи гибридных схем Р.П.Федоренко [15.5], предложенная Колганом, имеет вид

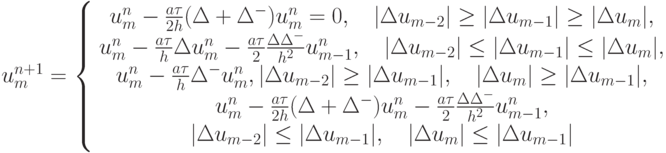
$u_m^{n + 1} = \left\{ \begin{array}{c} {u_m^{n} - \frac{a \tau}{2h}({\Delta}+ \Delta^{-})u_m^{n} = 0, \quad | {\Delta}u_{m - 2}| \ge |{\Delta}u_{m - 1}| \ge | {\Delta}u_m| }, \\ {u_m^{n} - \frac{a \tau}{h} \Delta u_m^{n} - \frac{a \tau}{2} \frac{{\Delta}\Delta^{-}}{h^2} u_{m - 1}^{n}, \quad | {\Delta}u_{m - 2}| \le |{\Delta}u_{m - 1}| \le | {\Delta}u_m| }, \\ {u_m^{n} - \frac{a \tau}{h} \Delta^{-}u_m^{n}, | {\Delta}u_{m - 2}| \ge |{\Delta}u_{m - 1}|, \quad | {\Delta}u_m| \ge |{\Delta}u_{m - 1}| }, \\ u_m^{n} - \frac{a \tau}{2h}({\Delta}+ \Delta^{-})u_m^{n} - \frac{a \tau}{2} \frac{\Delta \Delta^{-}}{h^2} u_{m - 1}^{n}, \\ |{\Delta}u_{m - 2}| \le |{\Delta}u_{m - 1}|, \quad | {\Delta}u_m| \le |{\Delta}u_{m - 1}| \\ \end{array} \right.$

Здесь использованы обозначения $\Delta u_{m} = u_{m + 1} - u_{m}$ , $\Delta ^{ -} u_{m} = u_{m} - u_{m - 1}$ , $(\Delta + \Delta ^{ -})u_{m} = u_{m + 1} - u_{m - 1}$ , $(\Delta \Delta ^{ -})u_{m} = \Delta (\Delta ^{ -})u_{m} = u_{m + 1} - 2u_{m} + u_{m - 1}$ .

Соответствующие шаблоны показаны на рисунках ниже.

Рассмотрим способ конструирования TVD - схемы. Произвольную четырехточечную схему (три точки на нижнем временном слое) можно представить в виде 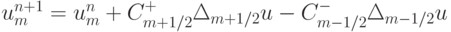$u_m^{n + 1} = u_m^{n} + C_{m + 1/2}^{+}\Delta_{m + 1/2} u - C_{m - 1/2}^{-}\Delta_{m - 1/2} u$ , где введены потоки $\Delta _{m + 1/2} u = u_{m + 1} - u_{m}, \Delta _{m - 1/2} u = u_{m} - u_{m - 1}$ . 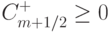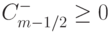Положим, что коэффициенты схемы удовлетворяют условиям $C_{m + 1/2}^{+} \ge 0$ , ${C_{m - 1/2}^{-} \ge 0}$ , для всех m. Тогда приведенная разностная схема является TVD - схемой. Покажем, что это так. Для этого вычислим полную вариацию

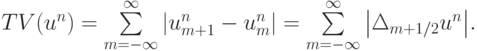
$TV(u^{n} ) = \sum\limits_{m = - \infty }^{\infty}{\left| {u_{m + 1}^{n} - u_m^{n}}\right|} = \sum\limits_{m = - \infty }^{\infty}{\left| {\Delta_{m + 1/2} u^{n}} \right|}.$

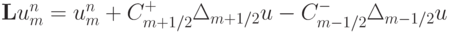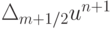Запишем разностную схему в операторном виде $u_m^{n + 1} = {\mathbf{L}}u_m^{n}$ , где ${\mathbf{L}}u_m^{n} = u_m^{n} + C_{{m} + 1/2}^{+}\Delta_{{m} + 1/2}u - C_{{m} - 1/2}^{-}\Delta_{{m} - 1/2} u$ . Покажем, что ${TV}(u^{n + 1} ) \le TV(u^{n} )$ , или ${TV}({\mathbf{L}}u^{n}) \le TV(u^{n})$ . Оценим величину $\Delta _{m + 1/2} u^{n + 1}$ , учитывая, что 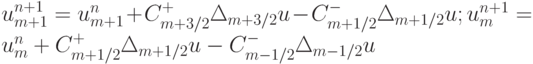$u_{{m} + 1}^{n + 1} = u_{m + 1}^{n} + C_{m + 3/2}^{+} \Delta_{m + 3/2} u - C_{m + 1/2}^{-}\Delta_{m + 1/2} u; u_m^{n + 1} = u_m^{n} + C_{m + 1/2}^{+}\Delta_{m + 1/2} u - C_{m - 1/2}^{-}\Delta_{m - 1/2} u$ . Тогда

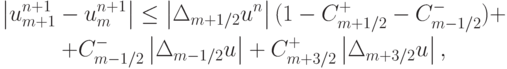
$\begin{gather*} \left| {u_{{m} + 1}^{n + 1} - u_m^{n + 1}}\right| \le \left| {\Delta_{{m} + 1/2} u^{n}}\right|(1 - C_{{m} + 1/2}^{+} - C_{{m} - 1/2}^{-}) + \\ + C_{{m} - 1/2}^{-} \left| {\Delta_{{m} - 1/2}u}\right| + C_{{m} + 3/2}^{+} \left|{\Delta_{{m} + 3/2} u}\right|, \end{gather*}$

откуда следует

$\begin{gather*} TV(u^{n + 1} )_m = \sum\limits_{- \infty }^{\infty} {\left|{\Delta_{{m} + 1/2} u^{n + 1}}\right|} \le \sum\limits_{- \infty}^{\infty}{(1 {- } C_{{m} - 1/2}^{+} - C_{{m} + 1/2}^{-})} \left|{\Delta_{{m} + 1/2} u^{n}}\right| + \\ + \sum\limits_{- \infty }^{\infty}{C_{{m} - 1/2}^{-} \left| \Delta_{{m} - 1/2} u\right| + \sum\limits_{- \infty }^{\infty}{C_{{m} + 3/2}^{+}}} \left|{\Delta_{{m} + 3/2} u}\right| \le \sum\limits_{- \infty }^{\infty}{\left| {\Delta_{{m} + 1/2} u^{n}}\right|} = TV(u^{n} ). \end{gather*}$

Дальше >>

Авторизоваться

Численные методы решения уравнений в частных производных

Лекция 5: Численное решение уравнений в частных производных гиперболического типа с большими градиентами решений

5.4. Метод коррекции потоков Бориса - Бука

5.5. TVD - схемы

Вопросы и ответы