Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1275 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 4:

Введение в методы численного решения уравнений газовой динамики
A
|
версия для печати
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >
Аннотация: Лекция не обязательна при первом прочтении книги. В лекции приводятся некоторые часто употребляемые численные методы решения уравнений газовой динамики. Особое внимание уделено идее конструирования разностных схем из семейства сеточно - характеристических
Ключевые слова: уравнения газовой динамики, расстояние, длина, пространство, неравенство, ПО, энергия, вектор, матрица, матричная форма, функция, энтропия, дивергентная форма, запись, координаты, связь, консервативная схема, система линейных алгебраических уравнений, собственный вектор, матрица перехода, базис, сеточно - характеристические разностные схемы, обобщение, метод неопределенных коэффициентов, отрезок, искусственная вязкость, численное интегрирование, неявная разностная схема, выражение, PICS, метод частиц в ячейках, алгоритм, Приращение, полное приращение, обыкновенное дифференциальное уравнение, метод Эйлера, значение, аппроксимация, частное решение

Рассмотренные в предыдущих лекциях разностные методы решения уравнений в частных производных демонстрировались на примере либо линейных задач, либо достаточно простых нелинейных уравнений с хорошо изученными свойствами. Такие задачи в реальной вычислительной практике обычно служат тестами для отработки методов решения более сложных нелинейных систем. Традиционным объектом приложения численных методов служат уравнения механики сплошной среды (МСС). Основных причин тому три. Первая — все математические модели МСС известны достаточно давно, хорошо исследованы и являются частью научной классики. Вторая — математические модели МСС нелинейны. Как правило, у линеаризованных уравнений очень узкая область применения. Третья — в результатах решения задач МСС на протяжении всего XX века была практическая заинтересованность, вызванная бурным развитием авиации, осуществлением наукоемких ядерных и космических программ в разных странах.

В данной книге ограничимся самой простой моделью МСС — уравнениями газовой динамики. Основная идея лекции — демонстрация идей и методов вычислительной математики, рассмотренных выше, в приложении к реальным задачам.

4.1. Формы записи одномерных уравнений газовой динамики

В основе построения математических моделей, описывающих поведение жидкостей и газов, лежит понятие о сплошной среде. Из молекулярной физики известно, что среда состоит из отдельных частиц (молекул, ионов, электронов, атомов), расстояние между которым существенно больше их собственных размеров. Длина свободного пробега частицы l (расстояние, пройденное частицей между двумя столкновениями) тем меньше, чем больше частиц заключено в единице объема, чем больше плотность среды. В механике жидкостей и газов рассматриваются среды, содержащие в единице объема большое количество частиц (много больше, чем число Авогадро — число частиц в одной грамм - молекуле вещества, N_A \approx 6 \cdot 10^{23} \quad (\mbox{г} \cdot \mbox{моль})^{- 1} ).

В таких средах можно рассматривать лишь некоторые усредненные характеристики, не занимаясь изучением поведения каждой частицы в отдельности. В этом предположении заключается идея модели сплошной среды, непрерывно заполняющей пространство.

Количественным критерием применимости приближения сплошной среды может служить неравенство 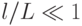l/L \ll 1, где L — характерный пространственный размер задачи (например, размер тела при внешнем обтекании потоком газа). В газах при нормальных условиях 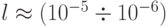l \approx (10^{- 5} \div 10^{- 6}) см, поэтому приведенное условие для тел с размером более 1 см выполняется с достаточной точностью. Предложение о сплошности среды, по - видимому, берет свое начало от Эйлера, впервые рассмотревшего газ как непрерывную деформируемую субстанцию. Не вдаваясь в особенности получения уравнений газовой динамики (этой теме посвящено большое количество литературы, [14.1], [14.2], [14.3]), приведем их в окончательный вид.

Эйлерова (недивергентная) форма одномерной системы уравнений газодинамики имеет вид

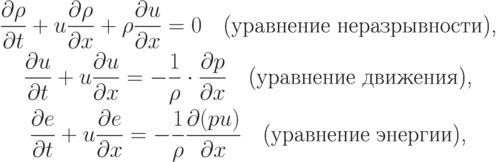\begin{gather*} \frac{{\partial}{\rho}}{{\partial}t} + u \frac{{\partial}{\rho}}{{\partial x}} + {\rho}\frac{{\partial}u}{{\partial}x} = 0 \quad \mbox{(уравнение неразрывности), }\\ \frac{{\partial}u}{{\partial}t} + u \frac{{\partial u}}{{\partial}x} = - \frac{1}{\rho} \cdot \frac{{\partial}p}{{\partial}x} \quad \mbox{(уравнение движения), } \\ \frac{{\partial}e}{{\partial}t} + u \frac{\partial e}{{\partial}x} = - \frac{1}{\rho} \frac{{\partial}(pu)}{{\partial}x} \quad \mbox{(уравнение энергии), } \end{gather*} ( 4.1)

где e — удельная энергия, равная

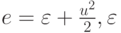
$ e = \varepsilon + \frac{u^2}{2}, \varepsilon $
удельная внутренняя энергия, u — скорость газа, \rho — плотность среды, p — давление, t — время, x — декартова координата. Эту же систему уравнений в частных производных можно представить в матричной (характеристической) форме

$ {\frac{{{\partial}{\mathbf{u}}}}{{\partial}t} + {\mathbf{A}} \frac{{{\partial}{\mathbf{u}}}}{{\partial}x} = 0, } $ ( 4.2)

где \mathbf{U} — вектор - столбец, \mathbf{A} — квадратная матрица 3 x 3.

Система замыкается уравнением состояния

f(\rho , \varepsilon , p) = 0,

которое, например, для идеального газа имеет вид

\frac{p}{{\rho}(\gamma - 1)} - \varepsilon = 0.

где \gamma — безразмерная постоянная, равная отношению теплоемкости газа при постоянном давлении и теплоемкости при постоянном объеме — постоянная адиабаты.

В системе, записанной в матричной форме (4.2), учтено, что давление есть функция температуры (или удельной внутренней энергии) и плотности 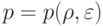p = p(\rho , \varepsilon ) следовательно,

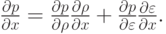
$ \frac{{\partial}p}{{\partial}x} = \frac{{\partial}p}{{\partial {\rho}}} \frac{{{\partial}{\rho}}}{{\partial}x} + \frac{{\partial}p}{{\partial \varepsilon }} \frac{{{\partial}\varepsilon }}{{\partial}x}. $

Не занимаясь выводом формул (это делается простыми алгебраическими преобразованиями), представим другие виды записи уравнения энергии, справедливые для приведенного выше уравнения состояния:

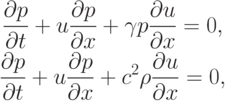
\begin{gather*} \frac{{\partial}p}{{\partial}t} + u \frac{{\partial p}}{{\partial}x} + \gamma p \frac{{\partial}u}{{\partial}x} = 0, \\ \frac{{\partial}p}{{\partial}t} + u \frac{{\partial p}}{{\partial}x} + c^2 {\rho}\frac{{\partial}u}{{\partial}x} = 0, \end{gather*}

где c = \sqrt{\gamma {p/{\rho}}} — адиабатическая скорость звука,

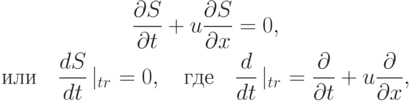
\begin{gather*} \frac{{{\partial}S}}{{\partial}t} + u \frac{{{\partial}S}}{{\partial}x} = 0, \\ \mbox{или} \quad \frac{dS}{dt} \left|_{tr}\right. = 0, \quad \mbox{где} \quad \frac{d}{dt} \left|_{tr}\right. = \frac{\partial }{{\partial}t} + u \frac{{\partial}}{{\partial}x}, \end{gather*}

S = m(\varepsilon \rho )^{1 - \gamma } — энтропия. Она, как следует из последней формулы, сохраняется вдоль траектории частицы идеального газа, т.е. на траектории уравнения

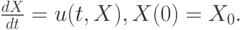
$ \frac{dX}{dt} = u(t, X), X(0) = X_0. $

Дивергентная форма уравнений газовой динамики получается при записи соответствующих законов сохранения в интегральной форме. Если затем совершить предельный переход, то дифференциальная запись уравнений будет

\begin{gather*} \frac{{\partial}{\rho}}{{\partial}t} + \frac{\partial }{{\partial}x}({\rho}u) = 0, \\ \frac{\partial}{{\partial}t}({\rho}u) + \frac{\partial}{{\partial}x}({\rho}u^2 + p) = 0, \\ \frac{\partial}{{\partial}t} \left[{{\rho}\left({\varepsilon + \frac{u^2}{2}}\right)}\right] + \frac{\partial}{{\partial}x} \left[{{\rho}u \left({\varepsilon + \frac{u^2}{2} + \frac{p}{\rho}}\right)}\right] = 0, \end{gather*} ( 4.3)

или в матричной форме

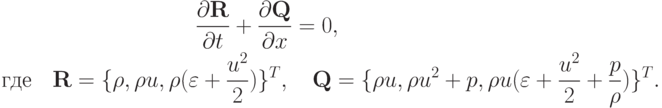
\begin{gather*} \frac{{{\partial}{\mathbf{R}}}}{{\partial}t} + \frac{{{\partial}{\mathbf{Q}}}}{{\partial}x} = 0, \\ \mbox{где} \quad {\mathbf{R}} = \{{\rho}, {\rho}u, {\rho}(\varepsilon + \frac{{u^2}}{2}) \}^{T}, \quad {\mathbf{Q}} = \{{\rho}u, {\rho}u^2 + p, \rho u(\varepsilon + \frac{{u^2}}{2} + \frac{p}{\rho}) \} ^{T} . \end{gather*}

Интегральная форма этих уравнений получается при использовании теоремы Гаусса - Остроградского

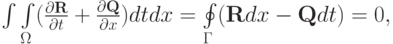
$ \int\int\limits_{\Omega}(\frac{{{\partial}{\mathbf{R}}}}{{\partial}t} + \frac{{{\partial}{\mathbf{Q}}}}{{\partial}x}){dtdx} = \oint\limits_{\Gamma}(\mathbf{R}dx - \mathbf{Q}dt) = 0, $

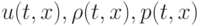где \Gamma — граница замкнутой области интегрирования \Omega в плоскости t, x. Здесь u(t, x), \rho (t, x), p(t, x) — скорость, плотность и давление газа соответственно. В механике сплошных сред вводится эйлерово и лагранжево описание поведения среды. В первом случае наблюдатель полагается неподвижным, например, стоящим на берегу реки. Соответственно расчетная сетка будет неподвижной (фиксированная эйлерова сетка). Во втором случае полагаем, что наблюдатель движется вместе со средой, например, находится на лодке, плывущей по течению реки. В этом случае лагранжева расчетная сетка будет двигаться вместе с частицами среды.

Лагранжева форма одномерных уравнений газовой динамики имеет вид

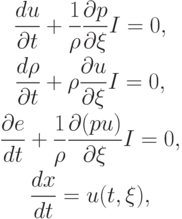
\begin{gather*} \frac{du}{{\partial}t} + \frac{1}{\rho} \frac{{\partial}p}{{\partial}\xi }I = 0, \\ \frac{{d {\rho}}}{{\partial}t} + {\rho}\frac{{\partial}u}{{\partial}\xi }I = 0, \\ \frac{{{\partial}e}}{dt} + \frac{1}{\rho} \frac{{\partial}(pu)}{{\partial}\xi }I = 0, \\ \frac{dx}{dt} = u(t, \xi ), \end{gather*}

где

$ I = \left({\frac{{\partial}x}{{\partial}\xi }}\right)^{- 1}, $
x и \xi соответственно эйлерова и лагранжева координаты, связь между которыми дается последним уравнением. Эта система в одномерном случае может быть записана в другом виде. Если ввести лагранжеву массовую координату \eta (\xi ), связанную с лагранжевой координатой \xi дифференциальным уравнением
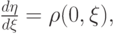
$ \frac{{d \eta }}{{d \xi }} = {\rho}(0, \xi ), $
в массовых координатах последняя система запишется как

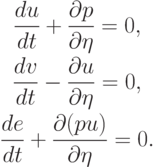\begin{gather*} \frac{du}{dt} + \frac{{\partial}p}{{{\partial}\eta }} = 0, \\ \frac{dv}{dt} - \frac{{\partial}u}{{\partial}\eta} = 0, \\ {\frac{de}{dt} + \frac{{\partial}(pu)}{{\partial}\eta} = 0.} \end{gather*} ( 4.4)

Эта система дополняется уравнениями, связывающими лагранжевы и эйлеровы координаты

$ \frac{dx}{dt} = u(t, \eta ), \quad \frac{{dx(0, \eta )}} {{d \eta }} = {v}(0, \eta ), $

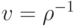где v = \rho ^{ - 1} — удельный объем.

Дальше >>
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

Вопросы и ответы

вопросов: 0